题目
(又是权限题,dbzoj 还要装洋葱上,本地数据大法好)
幼稚的思考过程
众所周知,qhy 是一个数据结构很菜的女孩子,所以我们来做一下这道树剖模板题(
其实刚开始我是想倒序跑的(后来发现我看错题了,每次询问只删当前的一条边而不是永久删)
后来想了想次小生成树也会 gg,所以去看题解了(
题解
我们将最开始在最小生成树上的边叫做树边,其它边叫做非树边。
容易知道,当删掉非树边的时候,最小生成树不变。
当删掉树边的时候,树会变成两个联通块,最小生成树存在当且仅当有边能连接两个联通块。
那我们去计算删掉一条边后最小能联通两个联通块的代价?(显然你还要带一个边集大小的复杂度,会 gg)
尝试反过来考虑,用一条非树边来计算有哪些树边可以被它替代。
如图所示:
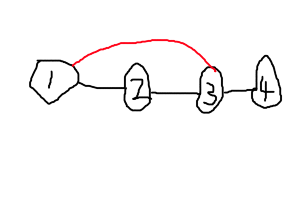
红边是一条非树边,易知,1-2,2-3 之间的树边是可以被红边替代的,而 3-4 之间的树边则不行,我们容易知道,一条非树边能替代它两个端点在树边上的一段区间。
因此我们可以用树剖维护最小生成树,将非树边的影响 update 到树边上,询问删除树边的时候只要 query 一下就行。
复杂度是 $O(nlog^2n)$
代码:
#include<bits/stdc++.h>
#define fo(i, a, b) for (int i = (a); i <= (b); ++i)
#define fd(i, a, b) for (int i = (a); i >= (b); --i)
#define edge(i, u) for (int i = head[u], v = e[i].v; i; i = e[i].nxt, v = e[i].v)
#define N 100505
#define KK 155
#define pb push_back
#define F first
#define S second
#define ll long long
#define inf 1000000007
#define mp std::make_pair
#define lowbit(x) (x & -x)
#define ls (k << 1)
#define rs (k << 1 | 1)
#define mod 10007
#define eps 1e-4
struct node{
int u, v, w, id;
bool fl;
friend bool operator < (node x, node y)
{
return x.w < y.w;
}
}p[N];
int q, n, m, cp, head[N], tot;//countpoint
int father[N];
inline int find (int x) {return x == father[x] ? x : father[x] = find(father[x]);}
int son[N], top[N], fa[N], sz[N], id[N], dfn[N], tim, dep[N];
struct edge{
int nxt, v;
}e[N << 1];
inline bool cmp (node x, node y) {return x.id < y.id;}
inline void addedge (int u, int v)
{
e[++tot] = (edge) {head[u], v};
head[u] = tot;
}
inline void dfs1 (int u, int fath)
{
dep[u] = dep[fath] + 1;
fa[u] = fath;
sz[u] = 1;
edge (i, u)
{
if (v == fath) continue;
dfs1(v, u);
sz[u] += sz[v];
if (!son[u] || sz[son[u]] < sz[v]) son[u] = v;
}
}
inline void dfs2 (int u, int tp)
{
top[u] = tp;
dfn[u] = ++tim;
if (son[u]) dfs2(son[u], tp);
edge (i, u)
{
if (v == fa[u] || v == son[u]) continue;
dfs2(v, v);
}
}
namespace seg{//segment_tree
int min[N << 2];
inline void update (int k, int l, int r, int L, int R, int val)
{
if (L <= l && r <= R) {min[k] = std::min(min[k], val); return;}
int mid = l + r >> 1;
if (L <= mid) update(ls, l, mid, L, R, val);
if (mid < R) update(rs, mid + 1, r, L, R, val);
}
inline int query (int k, int l, int r, int pos)
{
if (l == r) {return min[k];}
int mid = l + r >> 1;
if (pos <= mid) return std::min(min[k], query(ls, l, mid, pos));
else return std::min(min[k], query(rs, mid + 1, r, pos));
}
}
int valnow;
int main ()
{
scanf("%d %d", &n, &m);
fo (i, 1, m)
{
scanf("%d %d %d", &p[i].u, &p[i].v, &p[i].w);
p[i].id = i;
}
std::sort(p + 1, p + m + 1);
fo (i, 1, n) father[i] = i;
cp = 1;
memset(seg::min, 0x3f, sizeof seg::min);
fo (i, 1, m)
{
int fx = find(p[i].u);
int fy = find(p[i].v);
if (fx != fy)
{
father[fx] = fy;
p[i].fl = 1;
++cp;
addedge(p[i].u, p[i].v);
addedge(p[i].v, p[i].u);
valnow += p[i].w;
if (cp == n) break;
}
}
scanf("%d", &q);
if (cp < n)
{
fo (i, 1, q)
printf("Not connected\n");
return 0;
}
std::sort(p + 1, p + m + 1, cmp);
dfs1(1, 0);
dfs2(1, 1);
fo (i, 1, m)
if (!p[i].fl)//edge not in tree
{
int x = p[i].u, y = p[i].v;
while (top[x] != top[y])
{
if (dep[top[x]] > dep[top[y]]) std::swap(x, y);
seg::update(1, 1, n, dfn[top[y]], dfn[y], p[i].w);
// printf("[%d, %d] %d\n", dfn[top[y]], dfn[y], p[i].w);
y = fa[top[y]];
}
if (dep[y] < dep[x]) std::swap(x, y);
if (x != y) seg::update(1, 1, n, dfn[x] + 1, dfn[y], p[i].w);
// printf("[%d, %d] %d\n", dfn[x] + 1, dfn[y], p[i].w);
}
fo (i, 1, q)
{
int x;
scanf("%d", &x);
if (!p[x].fl)
printf("%d\n", valnow);
else
{
int now = (dep[p[x].u] < dep[p[x].v]) ? dfn[p[x].v] : dfn[p[x].u]; //边信息存在儿子节点
int ans = seg::query(1, 1, n, now);
// printf("%d\n", now);
// printf("query : %d ans = %d\n", now, ans);
if (ans == seg::min[0])
printf("Not connected\n");
else
printf("%d\n", valnow - p[x].w + ans);
}
}
return 0;
}
(因为 148 行的一个 p[x].w 打成了 p[i].w,我调试了一遍树剖两个 dfs 和线段树弄了一个半小时比赛的时候注意检查最简单的细节 QAQ,不然会调自闭的)
0 条评论