被概率冲昏的头脑~~~
我们先将样例在图上画下来:
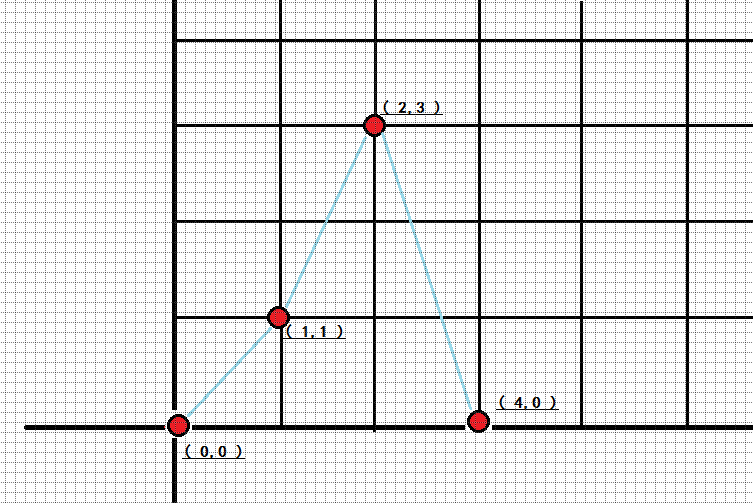
会发现,最大收益是:
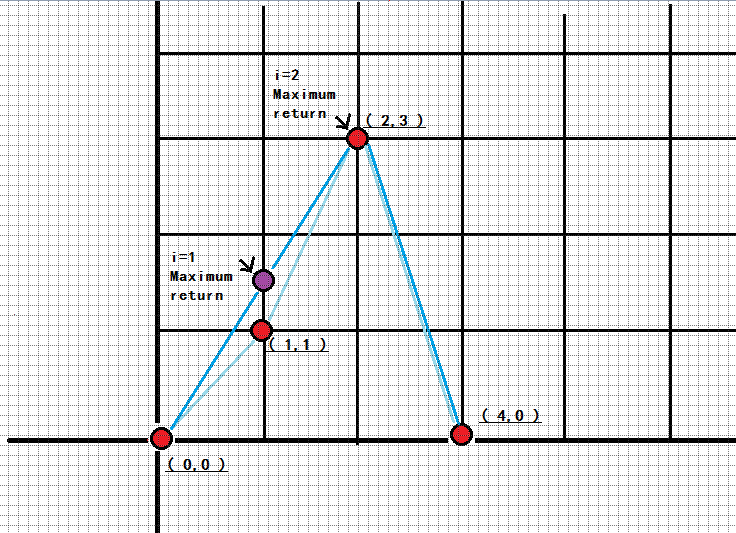
看出什么了吗?
这不就是凸包吗?
跑一遍凸包就好了呀,这些点中,如果 i 号点是凸包上的点,那么它的 ans 就是自己 (第二个点),不然的话,从上图来看,i 的 ans 肯定和他相邻的两个是凸包边界的点有关 (0 节点和 2 节点),那么怎么求这个 ans 呢?(第 x 号点为横坐标为 x 的点)
实际上我也不知道就是个期望公式啊!
l[i] 记录 i 号点往左走第一个为凸包边界的点 (如果 i 为 1 号,那么 l[i] 为 0,特殊的,如果 i 为 2 号,那么 l[i] 就是本身),r[i] 同理。当 l[x]==r[x] 时,x 时边界。
就是这个方程: (f[l[i]])*(r[i]-i)+f[r[i]]*(i-l[i])))/(r[i]-l[i]);
上面的方程上课时已讲,在此不再赘述 (实际上是不会证)
关于凸包,在这贴一波 YYB 大神的博客:传送门戳我 QwQ
#include<bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define RI register int
#define F 100000
using namespace std;
const int NS=1e5+5;
ll f[NS],l[NS],r[NS],hep[NS];
//f 如题,l[i]/r[i] 如上文,hep 为凸包
template <typename _Tp> inline void IN(_Tp&x){
char ch;bool flag=0;x=0;
while(ch=getchar(),!isdigit(ch))if(ch=='-')flag=1;
while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
if(flag)x=-x;
}
int main(){
int n,top=0;IN(n);hep[++top]=0;//注意先加入 0!
for(int i=1;i<=n;++i)IN(f[i]);
for(int i=1;i<=n+1;++i){//凸包
while(top>=2){
int a=hep[top],b=hep[top-1];
if(((f[a]-f[b])*(i-a))<((f[i]-f[a])*(a-b)))--top;
else break;
}hep[++top]=i;
}
for(int i=1;i<top;++i){
//中间的节点的 l,r 值都为 hep[i]/hep[i+1]
for(int j=hep[i]+1;j<hep[i+1];++j){
l[j]=hep[i],r[j]=hep[i+1];
}l[hep[i]]=hep[i],r[hep[i]]=hep[i];
}
for(int i=1;i<=n;++i){
ll ans=0;//记得 LL!
if(l[i]==r[i])ans=f[i]*F;//为边界,直接跳下最优
else ans=(F*(f[l[i]]*(r[i]-i)+f[r[i]]*(i-l[i])))/(r[i]-l[i]);//否则用方程算
printf("%lld\n",ans);
}return 0;
}
0 条评论