【题解】[Usaco2010 OPen]Triangle Counting 数三角形 LUOGU – 2992

题目戳这里

首先按极角排序，扫过去

对于当前扫到的点，连接它到原点的直线会把平面分割成两个半平面

对于直线左边的半平面（左边指的是给直线一个方向，比如是原点出发到当前点为正方向，左边半平面指的就是正半轴逆时针扫过的半平面）内的任意两个点与当前点构成的三角形都不覆盖原点

如图所示：

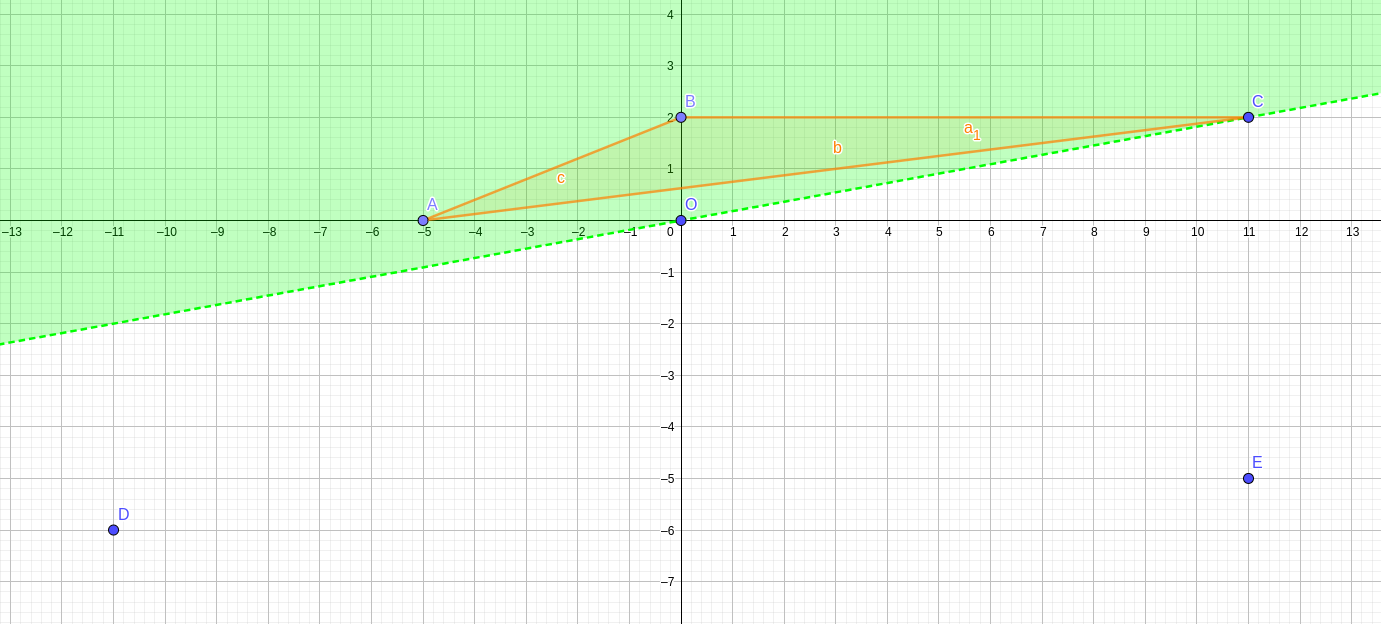
此图即为数据：

5 
-5 0 
0 2 
11 2 
-11 -6 
11 -5 

图中 $C$是极角最小的点 $(11, 2)$，绿色平面即为 $O->C$左边的半平面，该半平面覆盖了点 $A$和点 $B$，因此 $\triangle ABC$是一定不会过原点的

就这样扫过来，维护绿色半平面内包含的点数，设为 $cnt$，则每次答案就减去 $C _ {cnt} ^ 2$就行了

（初始时答案等于 $C _ n ^ 3$）

代码：

#include <bits/stdc++.h>

#define NS (100005)

typedef long long LL;

using namespace std;

const double PI = acos(-1);

template<typename _Tp> inline void IN(_Tp& dig)
{
    char c; bool flag = 0; dig = 0;
    while (c = getchar(), !isdigit(c)) if (c == '-') flag = 1;
    while (isdigit(c)) dig = dig * 10 + c - '0', c = getchar();
    if (flag) dig = -dig;
}

struct Point
{
    double x, y, r;
    Point() {x = y = r = 0;}
    Point(double a, double b)
    {
        x = a, y = b, r = atan2(b, a);
        if (r < 0) r += PI * 2;
    }
    bool operator < (const Point oth) const {return r < oth.r;}
} P[NS];

int n;

LL ans;

int main(int argc, char const* argv[])
{
    IN(n);
    for (int i = 1, a, b; i <= n; i += 1)
        IN(a), IN(b), P[i] = Point(a, b);
    if (n <= 2) puts("0"), exit(0);
    ans = 1ll * n * (n - 1) * (n - 2) / 6, sort(P + 1, P + 1 + n);
    double dr = PI;
    for (int i = 1, j = 1, cnt = 0; i <= n; i += 1)
    {
        dr += P[i].r - P[i - 1].r;
        while (j <= n && P[j].r < dr) cnt++, j++;
        if (dr >= PI * 2)
        {
            dr -= PI * 2;
            if (j > n) j = 1;
            while (j <= n && P[j].r < dr) cnt++, j++;
        }
        if (cnt >= 2) ans -= ((1ll * (cnt - 1) * (cnt - 2)) >> 1);
        cnt--;
    }
    printf("%lld\n", ans);
    return 0;
}