题目是这样的：给你 T 组数据，每组 2 个字符串 A,B 求 A 在 B 中出现次数 (超过 10⁶ 个字符)

所以只能用 KMP

简单介绍一下 KMP（刚学）

在字符串匹配的过程中，若使用 O(NM) 暴力算法，显然会有很多多余匹配的操作。比如 匹配 aaaaaaaaaaaaab 和 aaaab。前面那么多 a 你就一个个挨着匹配不累啊。所以有了 KMP 算法。

KMP 算法的主体思想是：利用 NEXT 数组在 A,B 的某一位匹配失败时主动将 B 串前移一定位数，跳过绝对不会出现匹配情况的串部分。而 NEXT 数组是什么呢？

NEXT[i] 表示 待匹配串 B 的长度为 i 的前缀 的 长度相同且字符相同（说白了就是完全相同）的前缀和后缀的最长长度。

如对于 ababcaba : NEXT[3]=1 ,NEXT[4]=2 ,NEXT[5]=0 ,NEXT[8]=3…

这样，当如图的情况时，我们可以让 B 串前移 NEXT[i-1] 位

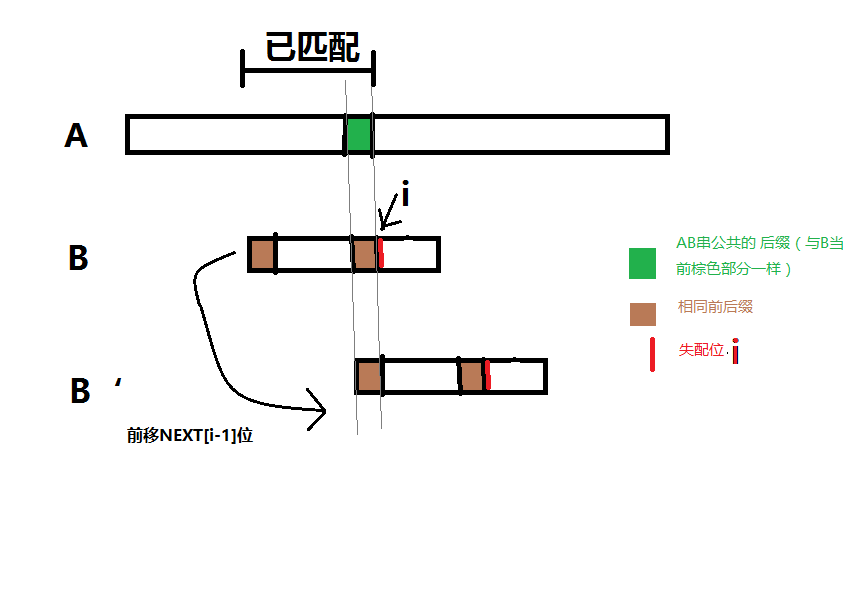
这样，我们就可以很快求出 B 是否为 A 的字串。

于是，现在最大的问题就是如何求 NEXT 数组

方法：若现在我们已经求出了 NEXT[i], 就会有如下的两种情况 (注意 NEXT 下标为长度而 B 为字符串的位)

a. B[i]==B[NEXT[i]+1], 此时 NEXT[i+1]=NEXT[i]+1;

b. B[i]!=B[NEXT[i]+1], 此时 NEXT[i+1] 可以由一种高深的方法得到：不断寻找 B 前 i 位的公共前后缀的公共前后缀… 直到某一个前缀的后一位与 B[i] 相同，NEXT[i+1]={此时的 NEXT}；

#include <iostream>
#include <cstdio>
#include <cstring>

#define MX 1000001
#define ML 10001

using namespace std;

int tot,nxt[ML];
char tar[MX],str[ML];

void getnext(int slen)
{
    int i=0,j=-1;
    nxt[0]=-1;
    while(i<slen)
    {
        if(j==-1||str[i]==str[j])nxt[++i]=++j;
        else j= nxt[j];
    }
}

int KMP(int slen,int tlen)
{
    int i=0,j=0,ans=0;
    while(i<tlen)
    {
        if(tar[i]==str[j]||j==-1)i++,j++;
        else j=nxt[j];
        if(j==slen)ans++,j=nxt[j-1],i--;
    }
    return ans;
}

int main()
{
    int t,slen,tlen;
    scanf("%d",&t);
    for(int w=1; w<=t; w++)
    {
        scanf("%s%s",str,tar);
        slen=strlen(str),tlen=strlen(tar);
        tot=0;
        getnext(slen);
        printf("%d\n",KMP(slen,tlen));
    }
    return 0;
}