题目链接_(:з」∠)_
这是 NOI 2016 D1T1
首先设 ai为以位置 i为左端点的形如 AA 串的个数
设 bi为以位置 i为右端点的形如 AA 串的个数
那么答案就等于:
n–1∑i=1ai+1×bi
于是就能 O(n2)暴力求出 a,b,拿到 95 分的好成绩了=。=
要是在考场上肯定是写暴力了,正解长了不止一倍,万一挂了还没 95 分呢
那 5 分怎么做呢?
首先枚举 AA 中 A 的长度 l(AA 的长度为 2l)
然后每 l个位置插个标记
那么每个 AA 串都会覆盖正好两个相邻的标记
于是反过来考虑相邻的两个标记对 a,b数组的贡献
设这两个标记的位置为 i,j(j=i+l)
求一下原串第 i个后缀和第 j个后缀的最长公共前缀 LCP,以及第 i个前缀和第 j个前缀的最长公共后缀 LCS
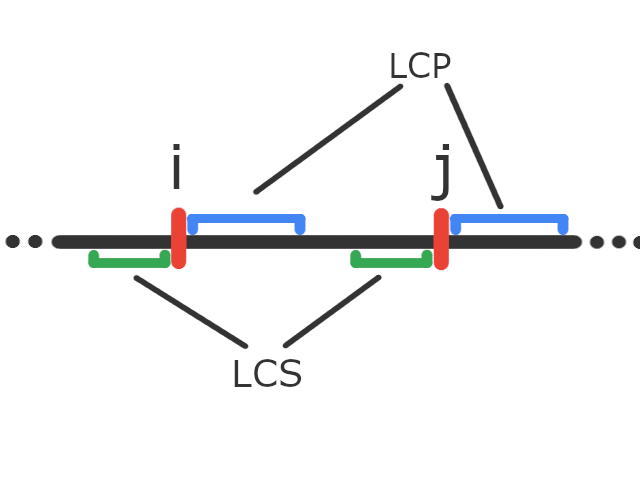
对于图中这种情况,LCP(蓝色部分)+LCS(绿色部分)是小与 l的(也就是 i,j之间的距离)
这种情况很显然不可能有 AA 能覆盖掉 i,j两个标记
如果是这种情况:
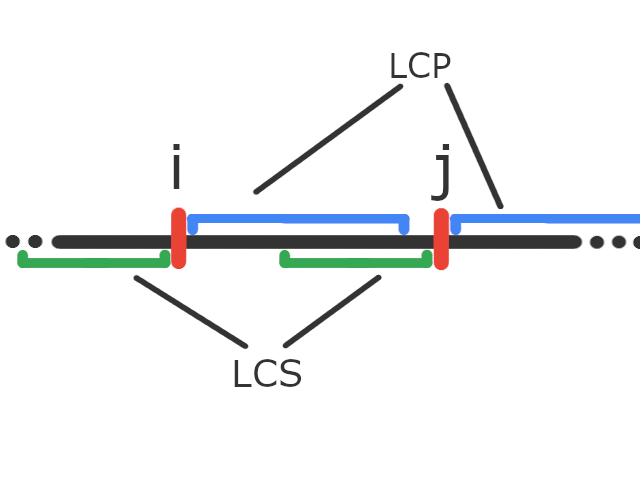
那么 AA 串就这么摆(右边图画不下了 QAQ):
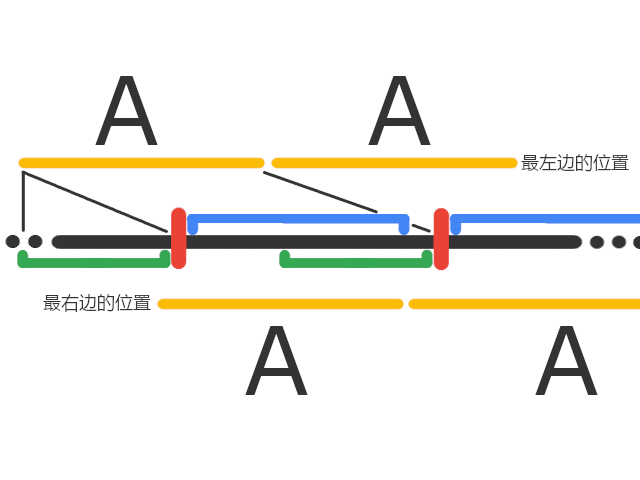
于是就知道相邻的两个标记对 a,b的贡献了
由于贡献是对一段区间上的,因此用差分维护一下就行了
求 LCP 和 LCS 就搞两个后缀数组,求 Height 再用 RMQ 维护
复杂度 O(nlog2n)
#include <bits/stdc++.h>
#define NS (60005)
#define LGS (19)
typedef long long LL;
using namespace std;
struct suffixArray
{
char s[NS];
int n, SA[NS], x[NS], y[NS], T[NS], H[NS], lg[NS], st[LGS][NS];
void init(char (&a)[NS])
{
memmove(s, a, sizeof(s)), n = strlen(s + 1);
memset(x, 0, sizeof(x)), memset(y, 0, sizeof(y));
}
void RSort(int p)
{
memset(T + 1, 0, sizeof(int) * p);
for (int i = 1; i <= n; i += 1) T[x[y[i]]]++;
for (int i = 1; i <= p; i += 1) T[i] += T[i - 1];
for (int i = n; i >= 1; i -= 1) SA[T[x[y[i]]]--] = y[i];
}
#define cmp(a, b) (y[a] == y[b] && y[(a) + l] == y[(b) + l])
void run()
{
for (int i = 1; i <= n; i += 1) x[i] = s[i] - 'a' + 1, y[i] = i;
int p = 26; RSort(p);
for (int l = 1, q = 0; q < n; l <<= 1, p = q)
{
q = 0;
for (int i = n - l + 1; i <= n; i += 1) y[++q] = i;
for (int i = 1; i <= n; i += 1)
if (SA[i] > l) y[++q] = SA[i] - l;
RSort(p), swap(x, y), q = x[SA[1]] = 1;
for (int i = 2; i <= n; i += 1)
if (cmp(SA[i], SA[i - 1])) x[SA[i]] = q;
else x[SA[i]] = ++q;
}
for (int i = 1, j, lcp = 0; i <= n; i += 1)
{
if (lcp) lcp--;
j = SA[x[i] - 1];
while (s[i + lcp] == s[j + lcp]) lcp++;
H[x[i]] = lcp;
}
for (int i = 2; i <= n; i += 1)
if (i == (1 << (lg[i - 1] + 1))) lg[i] = lg[i - 1] + 1;
else lg[i] = lg[i - 1];
for (int i = 1; i <= n; i += 1) st[0][i] = H[i];
for (int i = 1; (1 << i) <= n; i += 1)
for (int j = 1; j + (1 << i) - 1 <= n; j += 1)
st[i][j] = min(st[i - 1][j], st[i - 1][j + (1 << (i - 1))]);
}
int lcp(int l, int r)
{
l = x[l], r = x[r];
if (l > r) swap(l, r);
l++;
int k = lg[r - l + 1];
return min(st[k][l], st[k][r - (1 << k) + 1]);
}
} sa1, sa2;
int testcase, n, ad[NS], bd[NS];
char str[NS];
LL ans;
int main(int argc, char const* argv[])
{
scanf("%d", &testcase);
while (testcase--)
{
ans = 0, memset(ad, 0, sizeof(ad)), memset(bd, 0, sizeof(bd));
scanf("%s", str + 1), n = strlen(str + 1);
sa1.init(str), reverse(str + 1, str + 1 + n), sa2.init(str);
sa1.run(), sa2.run();
for (int l = 1; l <= (n >> 1); l += 1)
{
for (int i = 1; i + l <= n; i += l)
{
int l1 = min(l, sa1.lcp(i, i + l));
int l2 = min(l, sa2.lcp(n - i + 1, n - i - l + 1)) - 1;
if (l1 + l2 < l) continue;
ad[i - l2]++, ad[i + l1 - l + 1]--;
bd[i - l2 + (l << 1) - 1]++, bd[i + l + l1]--;
}
}
for (int i = 1; i <= n; i += 1)
ad[i] += ad[i - 1], bd[i] += bd[i - 1];
ad[n + 1] = bd[n + 1] = 0;
for (int i = 1; i < n; i += 1) ans += 1ll * bd[i] * ad[i + 1];
printf("%lld\n", ans);
}
return 0;
}



0 条评论