$Spaly$ 是不会用的,这辈子也不会用的。
这道题当然可以用 $Splay$ 做,然而不会。
于是考虑怎么来做这道题,我们先来观察一下所有的操作:
1. 插入操作:很普通的插入操作……
2. 单旋最小值:
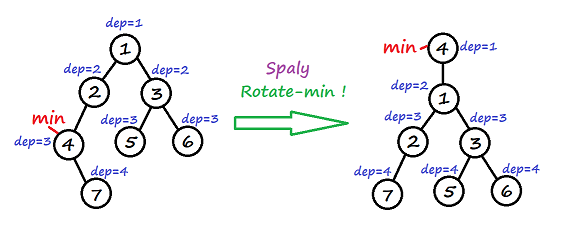
结点的深度的变化如下:
- 需要旋转的结点 $(4)$ :变为 $root$ ,深度变为 $1$ 。
- 需要旋转的结点的子树 $(7)$ :深度不变。
- 其他结点 $(1,2,3,5,6)$ :深度加 $1$ 。
3. 单旋最大值:
变化和上面的 “ 单旋最小值” 一样。
4.5 删除最大/最小值
先将需要删除的 最大/最小值 转到树根,这个时候我们将树根删掉,可以发现整棵树的深度全部都减了 $1$ ,一起计算上旋转造成的深度的影响会得到:
- 删掉的结点的子树 $(7)$ :深度减 $1$
- 其他节点 $(1,2,3,5,6)$ :深度不变
发现深度的变化也不是很大,于是我们考虑用线段树维护每一个节点的深度。
线段树不易寻找最大/最小值,这个地方我们用 $set$ 来辅助即可,操作的时候更新一下 $set$ 中树的形态就好。
线段树的要求很低,一个很普通的兹磁区间修改的线段树即可:
struct Segment_Tree{
#define mid ((l+r)>>1)
int dep[N<<2];
inline void pushdown(int x,int l,int r){
if(dep[x]){
dep[x<<1]+=dep[x],dep[x<<1|1]+=dep[x],dep[x]=0;
}return;
}
void add(int x,int l,int r,int L,int R,int res){
if(L<=l&&r<=R){dep[x]+=res;return;}
pushdown(x,l,r);
if(L<=mid)add(x<<1,l,mid,L,R,res);
if(R>mid)add(x<<1|1,mid+1,r,L,R,res);
}
void change(int x,int l,int r,int pos,int res){
if(l==r){dep[x]=res;return;}
pushdown(x,l,r);
if(pos<=mid)change(x<<1,l,mid,pos,res);
else change(x<<1|1,mid+1,r,pos,res);
}
int query(int x,int l,int r,int pos){
if(l==r)return dep[x];
pushdown(x,l,r);
if(pos<=mid)return query(x<<1,l,mid,pos);
else return query(x<<1|1,mid+1,r,pos);
}
}T;
1. 插入操作的实现:
std::set<int> Spaly;
inline int Insert(int x){
std::set<int>::iterator it=Spaly.insert(x).first;
if(!root){//还没有树根
T.change(1,1,tmp,x,1);//修改 x 的深度
root=x;return 1;//深度为 1
}
if(it!=Spaly.begin()){//不是最小值,所以可能成为其他结点的右儿子
if(!ch[*--it][1])ch[fa[x]=*it][1]=x;//成为右儿子
*it++;//维持 it 不变
}
if(!fa[x])ch[fa[x]=*++it][0]=x;//成为右儿子失败,于是成为左儿子
int dep_x=T.query(1,1,tmp,fa[x])+1;//x 的深度就是它父节点的深度加 1
T.change(1,1,tmp,x,dep_x);//在线段树中修改 x 的深度
return dep_x;//题目要求
}
2. 单旋最小/最大值的实现:
inline int Rotate_min(){
int x=*Spaly.begin(),ans=T.query(1,1,tmp,x);//获取当前的最小值和需要返回的答案
if(x==root)return 1;//是根就直接返回
if(x+1<fa[x])T.add(1,1,tmp,x+1,fa[x]-1,-1);//x 有子树,先给 x 的子树的深度整体减 1
T.add(1,1,tmp,1,tmp,1);//整棵树深度加 1,这个时候 x 的子树深度不变了
ch[fa[x]][0]=ch[x][1],fa[ch[x][1]]=fa[x];//将 x 的子树接到 x 的父亲上
ch[x][1]=root,fa[root]=x,root=x;//更新 root
T.change(1,1,tmp,x,1);//修改 x 的深度,变为 1
return ans;//题目要求
}
inline int Rotate_max(){//与上面的 Rotate_min 操作同理
int x=*Spaly.rbegin(),ans=T.query(1,1,tmp,x);
if(x==root)return 1;
if(x-1>fa[x])T.add(1,1,tmp,fa[x]+1,x-1,-1);
T.add(1,1,tmp,1,tmp,1);
ch[fa[x]][1]=ch[x][0],fa[ch[x][0]]=fa[x];
ch[x][0]=root,fa[root]=x,root=x;
T.change(1,1,tmp,x,1);
return ans;
}
3. 删除最小/最大值的实现:
inline void Delete_min(){
printf("%d\n",Rotate_min());//先旋上来,按照题目要求输出
T.add(1,1,tmp,1,tmp,-1);//整棵树的深度发生变化
Spaly.erase(root),root=ch[root][1],fa[root]=0;//更新 root
}
inline void Delete_max(){//与上面的 Delete_min 操作同理
printf("%d\n",Rotate_max());
T.add(1,1,tmp,1,tmp,-1);
Spaly.erase(root),root=ch[root][0],fa[root]=0;
}
Code:
#include<set>
#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
const int N=1e5+2;
const int inf=1e9+9;
int m,tmp,v[N],a[N],op[N];
template <typename _Tp> inline void IN(_Tp&x){
char ch;bool flag=0;x=0;
while(ch=getchar(),!isdigit(ch))if(ch=='-')flag=1;
while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
if(flag)x=-x;
}
struct Segment_Tree{
#define mid ((l+r)>>1)
int dep[N<<2];
inline void pushdown(int x,int l,int r){
if(dep[x]){
dep[x<<1]+=dep[x],dep[x<<1|1]+=dep[x],dep[x]=0;
}return;
}
void add(int x,int l,int r,int L,int R,int res){
if(L<=l&&r<=R){dep[x]+=res;return;}
pushdown(x,l,r);
if(L<=mid)add(x<<1,l,mid,L,R,res);
if(R>mid)add(x<<1|1,mid+1,r,L,R,res);
}
void change(int x,int l,int r,int pos,int res){
if(l==r){dep[x]=res;return;}
pushdown(x,l,r);
if(pos<=mid)change(x<<1,l,mid,pos,res);
else change(x<<1|1,mid+1,r,pos,res);
}
int query(int x,int l,int r,int pos){
if(l==r)return dep[x];
pushdown(x,l,r);
if(pos<=mid)return query(x<<1,l,mid,pos);
else return query(x<<1|1,mid+1,r,pos);
}
}T;
struct Spaly_Tree{
std::set<int> Spaly;
int root,fa[N],ch[N][2];
inline int Insert(int x){
std::set<int>::iterator it=Spaly.insert(x).first;
if(!root){
T.change(1,1,tmp,x,1);
root=x;return 1;
}
if(it!=Spaly.begin()){
if(!ch[*--it][1])ch[fa[x]=*it][1]=x;
*it++;
}
if(!fa[x])ch[fa[x]=*++it][0]=x;
int dep_x=T.query(1,1,tmp,fa[x])+1;
T.change(1,1,tmp,x,dep_x);
return dep_x;
}
inline int Rotate_min(){
int x=*Spaly.begin(),ans=T.query(1,1,tmp,x);
if(x==root)return 1;
if(x+1<fa[x])T.add(1,1,tmp,x+1,fa[x]-1,-1);
T.add(1,1,tmp,1,tmp,1);
ch[fa[x]][0]=ch[x][1],fa[ch[x][1]]=fa[x];
ch[x][1]=root,fa[root]=x,root=x;
T.change(1,1,tmp,x,1);
return ans;
}
inline int Rotate_max(){
int x=*Spaly.rbegin(),ans=T.query(1,1,tmp,x);
if(x==root)return 1;
if(x-1>fa[x])T.add(1,1,tmp,fa[x]+1,x-1,-1);
T.add(1,1,tmp,1,tmp,1);
ch[fa[x]][1]=ch[x][0],fa[ch[x][0]]=fa[x];
ch[x][0]=root,fa[root]=x,root=x;
T.change(1,1,tmp,x,1);
return ans;
}
inline void Delete_min(){
printf("%d\n",Rotate_min());
T.add(1,1,tmp,1,tmp,-1);
Spaly.erase(root),root=ch[root][1],fa[root]=0;
}
inline void Delete_max(){
printf("%d\n",Rotate_max());
T.add(1,1,tmp,1,tmp,-1);
Spaly.erase(root),root=ch[root][0],fa[root]=0;
}
}S;
int main(){
IN(m);
for(int i=1,x;i<=m;++i){
IN(op[i]);
if(op[i]==1)IN(x),v[++tmp]=a[i]=x;
}
std::sort(v+1,v+1+tmp);
for(int i=1;i<=m;++i)
if(op[i]==1)a[i]=std::lower_bound(v+1,v+1+tmp,a[i])-v;
for(int i=1;i<=m;++i){
if(op[i]==1)printf("%d\n",S.Insert(a[i]));
if(op[i]==2)printf("%d\n",S.Rotate_min());
if(op[i]==3)printf("%d\n",S.Rotate_max());
if(op[i]==4)S.Delete_min();
if(op[i]==5)S.Delete_max();
}
return 0;
}
0 条评论