自己姿势太低乱搞的时候只会构造,不会求最小
题解
首先显然只要有黑色格子就有方案。
然后我在搞的时候尝试证明一些类似充分必要的东西转换条件但是没想到= =
果然是太垃圾了只能去看题解
然后就会发现跟什么充分必要没啥关系
首先我们会发现,如果某一列有一个白色格子,它一定会被覆盖至少一次
当且仅当有一行全黑的时候,记此时操作数为 $x$,剩余 $y$列有白色格子,那么答案就是 $x+y$
关键就在这里了,你不论什么方案在变黑整个矩阵之前你必须要使一行全黑,顺着这个思路我们就会想到枚举这个变成全黑的行 $i$
若这一行的第 $j$列是白色的,我们就会想办法把它变黑,因为每次操作对于一行来说最多增加一个黑色,所以我们只需要考虑这一列,但是要让 $(i,j)$变黑我们还需要让第 $i$列有黑色的,如果没有的话我们也可以通过一步让第 $i$列至少有一个是黑色的。
如果你思路清晰的话容易看出上面的步骤都是最小的,但是同样的,我们在填充这一行为黑色之后还要看有多少列是有白色的,但是因为刚刚的操作是不会对没有全黑的列的数目产生影响的 (不可能增加,因为还没有全黑的行,也不可能减少,因为上面的填充都是基于增加黑色的),所以可以知道这是最小的方案。
还有一个彩蛋,我照着这个做了之后,结果获得了 $70$分的玄学成绩,于是我调了五年都没发现我的错误,直到我注意到别人代码的读入都不是快读而我用了快读,我开始害怕我难道快读写错了。
后来我下了数据,发现了一个惊天大秘密
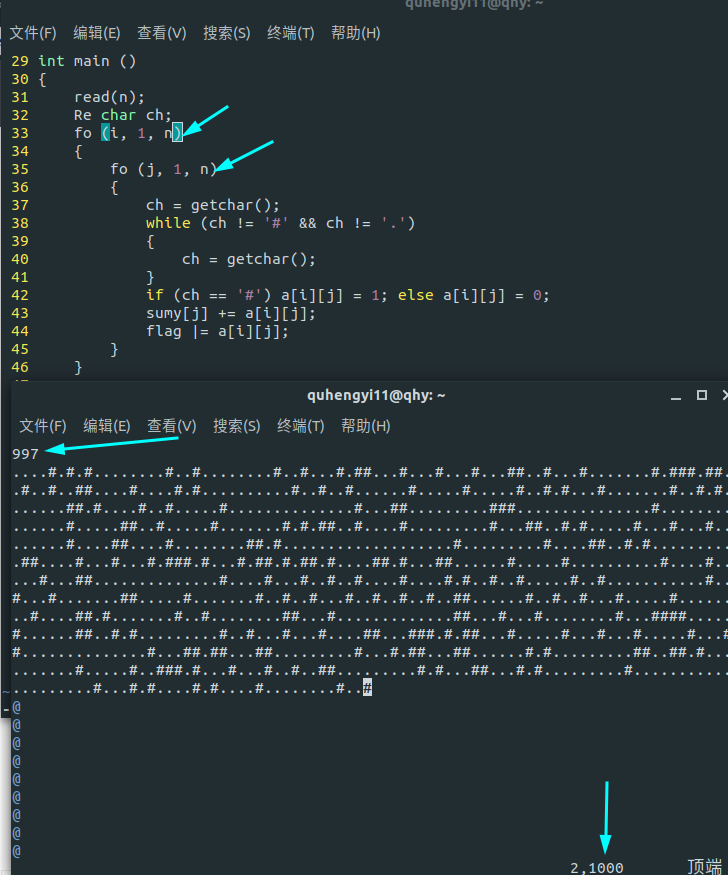
你一个 $997\times 997$的矩阵为什么一行有 $1000$个数
然后我快读亡了
后来我发现在讨论里已经有人说了这事= =
哎,就算是为自己 $rp$守恒做贡献了 $QAQ$
#include<bits/stdc++.h>
#define Re register
#define fo(i, a, b) for (Re int i = (a); i <= (b); ++i)
#define fd(i, a, b) for (Re int i = (a); i >= (b); --i)
#define edge(i, u) for (Re int i = head[u], v = e[i].v; i; i = e[i].nxt, v = e[i].v)
#define pb push_back
#define F first
#define S second
#define ll long long
#define inf 1000000007
#define mp std::make_pair
#define mod 2000000007
#define eps 1e-4
#define lowbit(x) (x & -x)
#define N 1005
#define ls (u << 1)
#define rs (u << 1 | 1)
#define cl(arr) memset(arr, 0, sizeof arr)
inline void read (int &x)
{
x = 0;
Re char ch = getchar();
while (!isdigit(ch)) ch = getchar();
while (isdigit(ch)) x = (x << 3) + (x << 1) + ch - '0', ch = getchar();
}
int a[N][N], sumy[N], res, ans = inf, n;
bool flag = 0;
char s[N];
int main ()
{
read(n);
Re char ch;
fo (i, 1, n)
{
scanf("%s", s + 1);
fo (j, 1, n)
{
// ch = getchar();
// while (ch != '#' && ch != '.') ch = getchar();
a[i][j] = (s[j] == '#');
sumy[j] += a[i][j];
flag |= a[i][j];
}
}
if (!flag) { printf("-1\n"); return 0; }
fo (i, 1, n) if (sumy[i] < n) ++res;
// printf("%d", res);
fo (i, 1, n)
{
int now = res;
bool fl = sumy[i];
fo (j, 1, n)
if (!a[i][j]) ++now;
now += (!(bool)sumy[i]);
// printf("%d ", now);
ans = std::min(ans, now);
}
printf("%d\n", ans);
return 0;
}
0 条评论