题意:给定一个数字 x(x<=105),不停得把数字得最后几位放到最前面去。求最多可以产生多少中不同得数字,求出这些数字与原数字比较大于、等于、小于的个数。
思路:每一个可能得数字就是:将原字符串自身复制一遍之后在其中截取的一段,其长度等于原数字长。 我们可以借助倍增、DC_3 或者扩展 KMP 求出复制后每个后缀与原字符串的最长公共前缀长度。(受限于本题的时间限制和数据范围,倍增光荣牺牲) 设 X 为原串自我复制一次后的字符串。如果X的后缀A和原字符串X的最长公共前缀长度为k, 那么比较A和X的大小就只需要比较A[k]和X[k]。这样就可以在O(lenX)时间内求出:X的每个长度为len的后缀和X的大小关系。 需要注意的是:如果X的后缀A和X的最长公共前缀长度k>=lenX/2, 那么我们就人为 X 和 A 相等。因为真正生成的数字只是 A 的前 lenX/2 位。
还有一个问题:如何处理字符串重复的问题?自己多写几个样例就会发现:字符串重复的次数总是等于原字符串的循环节数。证明:如果将串 Ab 经过移动变为 bA, 且 Ab==bA, 那么
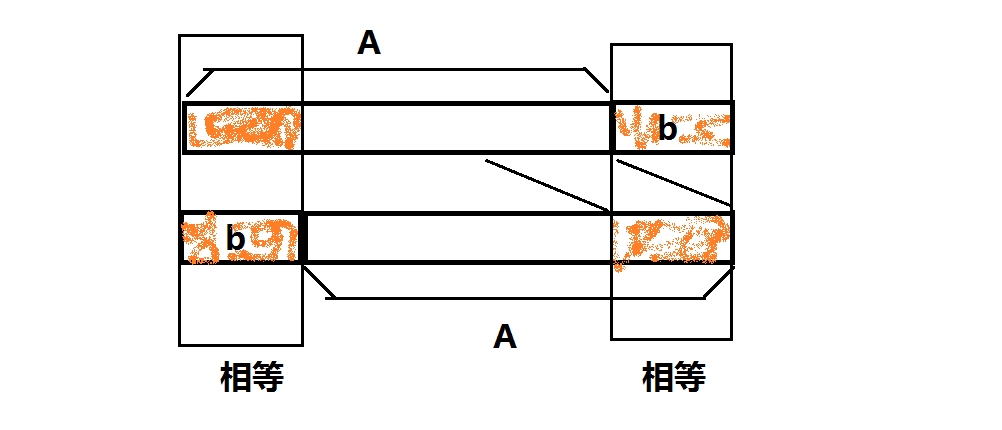
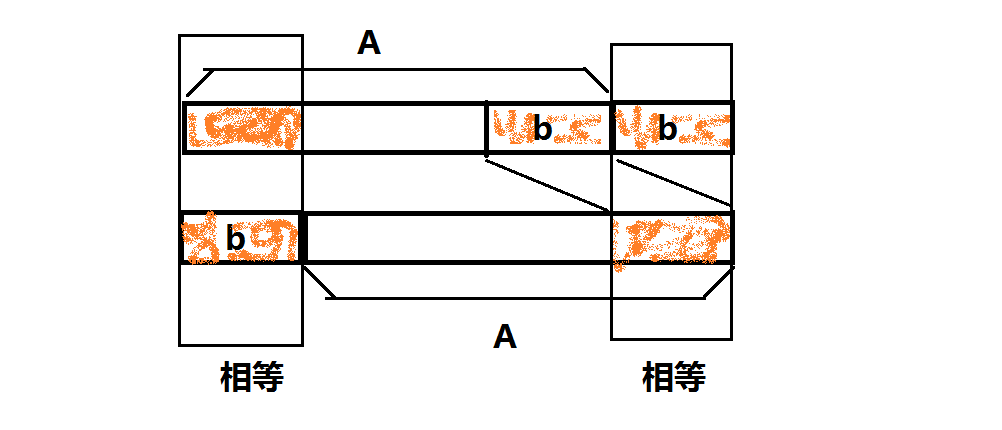
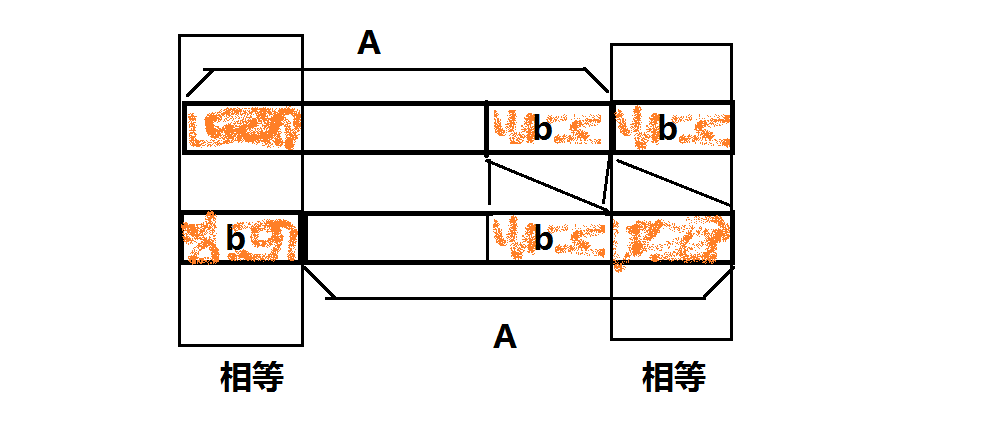
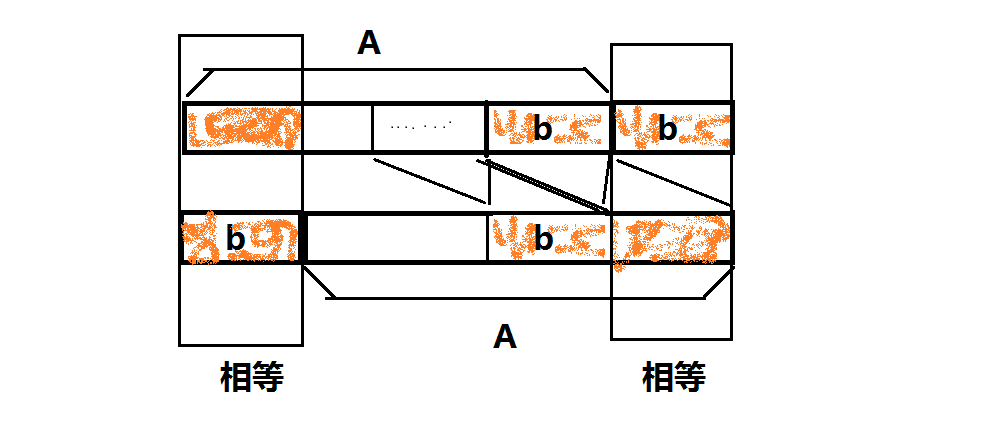
依此类推。
所以每发生一次 Ab==bA(b 尽可能短), 则原串的循环节数就会多一。同理推知,原串有 w 个循环节则会发生 w 次 Ab==bA。因为原串有 w 个循环节,所以对于每个循环节中的第 i 个数字 b[i], 如果它在操作时出现在串的末尾,那么一定会对应一个不同答案。又因为有 w 个循环节,所以每个答案出现了 w 次,所以只需要将答案数除以 w 即可。w 可以结合 kmp 的 next 数组在 O(n) 时间复杂度内求出。
在这里推荐几扩展(拓展)kmp 的教程:
教程 1
教程 2
#include <iostream>
#include <cstdio>
#include <cstring>
#define MX 100001
char src[MX*2],tmp[MX*2];
int nxt1[MX*2],nxt2[MX*2];
int big,sma,equ,dv;
using namespace std;
void getnext1(int *dis,char *str) //普通 kmp
{
int j=0,len=strlen(str);
dis[j]=0;
for(int i=1;i<len;i++)
{
while(j&&str[i]!=str[j])j=dis[j-1];
if(str[i]==str[j])j++;
dis[i]=j;
}
}
void getnext2(int *dis,char *str) //扩展 kmp
{
int len=strlen(str);
int k=0,i=1;
dis[0]=len;
while(k+1<len&&str[k]==str[k+1])k++;
dis[1]=k,k=1;
while(++i<len/2)
{
int mxr=k+dis[k]-1;
dis[i]=min(dis[i-k],max(mxr-i+1,0));
while(i+dis[i]<len&&str[dis[i]]==str[i+dis[i]])++dis[i];
if(i+dis[i]>k+dis[k])k=i;
}
}
void getans(int len)
{
big=sma=equ=0;
for(int i=0;i<len;i++)
{
if(nxt2[i]>=len)equ++;
else if(src[nxt2[i]]<src[i+nxt2[i]])big++;
else sma++;
}
}
int main()
{
int t,len;
scanf("%d",&t);
for(int w=1;w<=t;w++)
{
memset(src,0,sizeof(src)),memset(nxt1,0,sizeof(nxt1)),memset(nxt2,0,sizeof(nxt2));
scanf("%s",src);
len=strlen(src);
memmove(tmp,src,sizeof(src));
strcat(src,tmp);
getnext1(nxt1,tmp),getnext2(nxt2,src),getans(len);
dv=len%(len-nxt1[len-1]) == 0?len/(len-nxt1[len-1]):1; //利用 next 数组求出循环节数
cout<<"Case "<<w<<": "<<sma/dv<<" "<<equ/dv<<" "<<big/dv<<endl;
}
return 0;
}
0 条评论