洛谷 “新创无际夏日公开赛—-幻想乡的西瓜”T3

题意：将球体沿俯视图的两条半径切去一个扇形，求正视图中球的内部部分占总可视面积的百分比，如图为俯视图，正视图面向 0°的位置。两条半径的极角为 a,b∈[0,360] 的整数，从若 x∈[a,b] 则 x 对应的半径已被切去。如图:

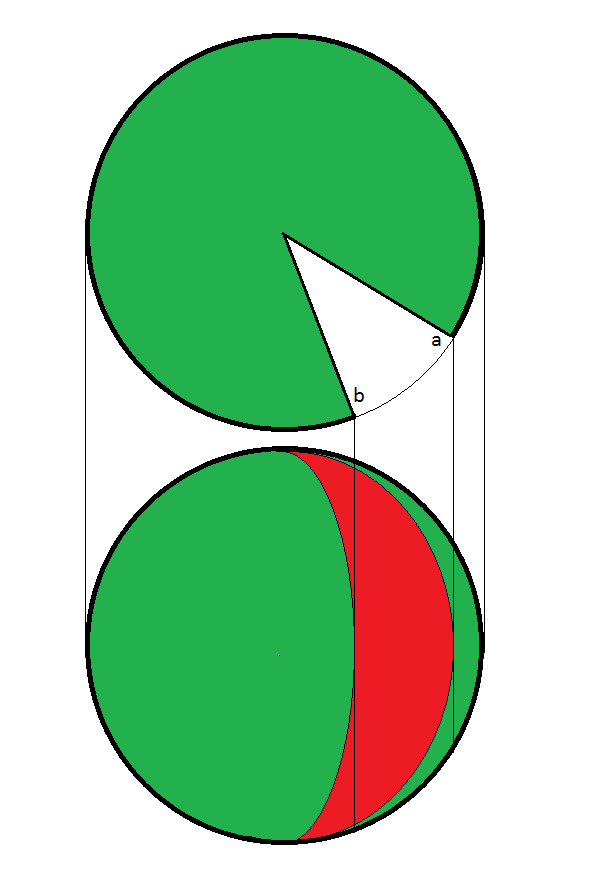
此题的分类讨论较多。设两条半径的极角分别为 a,b(a,b∈[0,360]):

则可以按 a,b 所在的四个象限及 a,b 的大小关系分为 20 类。
下面讨论对于某一分类，如何确定面积。由于切面为两个半圆，所以在空间中它也是两个圆。

引理 1：圆在空间中对于任意平面的平行投影为椭圆或线段。

引理 2：设一椭圆的长短轴长度分别为 p,q, 则 $S=\pi pq$

因此，我们可以利用引理 1、2 求出切面的正视图面积，求出面积差，进而求出答案。

需要注意的是，某些情况下全面积会由于切去部分而减少，如 a=0,b=180 的情况。

#include <iostream>
#include <cstdio>
#include <cmath>
#define pi 3.1415926535
using namespace std;
double dutohu(int x){return pi/180*x;}
double getarea(int a,int b)
{
    double s1,s2;
    s1=abs(pi*1*cos(dutohu(90-a)));
    s2=abs(pi*1*cos(dutohu(90-b)));
    if(a>=0&&a<90){
        if(b>=0&&b<a)return (s2/2)/(s1/2);
        else if(b>=a&&b<90)return (s2/2-s1/2)/pi;
        else if(b>=90&&b<180)return max(s2/2-s1/2,0.0)/(pi/2+max(s2/2,s1/2));
        else return 0;
    }
    else if(a>=90&&a<180){
        if(b>=0&&b<90)return s2/2/(pi/2);
        else if(b>=90&&b<a)return 1;
        else return 0;
    }
    else if(a>=180&&a<270){
        if(b>=0&&b<90)return (s1/2+s2/2)/(s1/2+pi/2);
        else if(b>=90&&b<a)return 1;
        else if(b>=a&&b<270)return 0;
        else return max(s1/2-s2/2,0.0)/(pi/2+max(s1/2,s2/2));
    }
    else if(a>=270&&a<360){
        if(b>=0&&b<90)return (s1+s2)/pi/2;
        else if(b>=90&&b<180)return (s1/2+s2/2)/(pi/2+s2/2);
        else if(b>=180&&b<270)return (s1/2)/(pi/2);
        else if(b>=270&&b<a)return s1/s2;
        else return (s1/2-s2/2)/pi;
    }
}
int main(){
    int t,a,b;
    scanf("%d",&t);
    for(int w=1;w<=t;w++){
        scanf("%d%d",&a,&b);
        printf("%.1f",getarea(a,b)*100);
        puts("%");
    }
    return 0;
}