【算法】卡特兰数 — Iris

同步发表于 博客园

基础知识

卡特兰数的式子

$$
\begin{aligned}
&h(n)=\sum_{i=0}^{n-1}h(i)\cdot h(n-i-1)\\
&h(n)=\frac{h(n-1)\cdot(4n-2)}{n+1}\\
&h(n)=\frac{\binom{2n}{n}}{n+1}=\frac{\binom{2n+1}{n}}{2n+1}
\end{aligned}
$$

卡特兰数的例子

• 合法出栈入栈操作序列。
• 合法括号序列。
• 凸多边形划分为三角形的方案数。

拓展

广义卡特兰数

似乎网上有相关论文，此处仅提及 FJOI 2020 D2T2 题目的例子浅显地了解一下。

将 $m$ 边凸多边形划分为 $n$ 个 $k$ 边形的方案 ( $m=nk-2(n-1)$ )

可以推导递推式
$$
h(n)=\sum_{S}\prod_{x\in S} h(x)\ [\ |S|=k-1,\sum_{x\in S}x=n-1]
$$
也可以用生成函数表示
$$
H(n)=xH^{k-1}(n)+1
$$

还可以将划分方案映射为序列

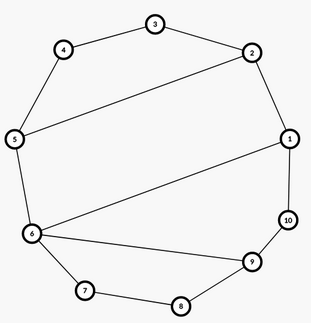
我们以十边形划分为 $4$ 个四边形为例，给出映射的规则：

从 $1$ 号点出发，依次遍历所有顶点，每抵达一个顶点，记为 $+1$，若当前顶点有指向编号更小的顶点的弦，则把划分出的一块全部割掉，那么此时边数的变化是减少了 $k-1$ 条边，然后增加了当前弦这一条边，故记为 $-(k-2)$。

特别的，我们把 $n$ 与 $1$ 的连边看作弦处理。

那么一个合法的划分方案将映射为一个由 $n$ 个 $-(k-2)$，$nk-2n+1$ 个 $+1$ 组成的前缀和为正的序列。

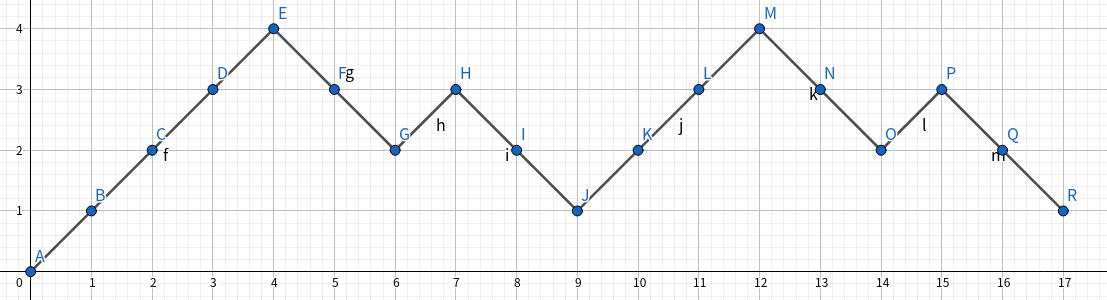
直接由 Raney 引理 得到方案数为 $\dfrac{\binom{nk-n+1}{n}}{nk-n+1}$.

Raney 引理

一个环 $x_1,x_2,…,x_n$，满足 $∑x_i=1$，在将它裂开形成的 $n$ 条可能的链中，恰有一条满足所有前缀和都是正数。

可以用于推导卡特兰数的一个通项式 $\dfrac{\binom{2n+1}{n}}{2n+1}$.

首先卡特兰数的等价于一个长为 $2n$，由 $n$ 个 $1$ 和 $n$ 个 $-1$ 组成前缀和非负的序列的方案数。

加入一个 $1$ 使得 $2n+1$ 个数的和是 $1$，以使用 Raney 引理。

首先这 $2n+1$ 个数的排列方案是 $\binom{2n+1}{n}$，而由引理可知，每 $2n+1$ 个循环同构的排列方式只有 $1$ 种合法。

故方案数为 $\dfrac{\binom{2n+1}{n}}{2n+1}$，然后因为加入一个 $1$ 新序列要求所有前缀和为正，所以序列首一定是 $1$，那么和满足卡特兰数含义的序列其实就是一一对应的。