论如何让 AC 代码爆 0(然后被 CY 老师罚款)
T1:frog
题意:
有一个点坐标在实数范围内的凸多边形,有一只青蛙从一号顶点开始跳,每次可以从任意一个顶点跳到任意一个顶点。求这只青蛙不重复遍历多边形的每个顶点的最少跳跃距离和。节点数小于等于 720(其实 100000+也可以做)
思路:
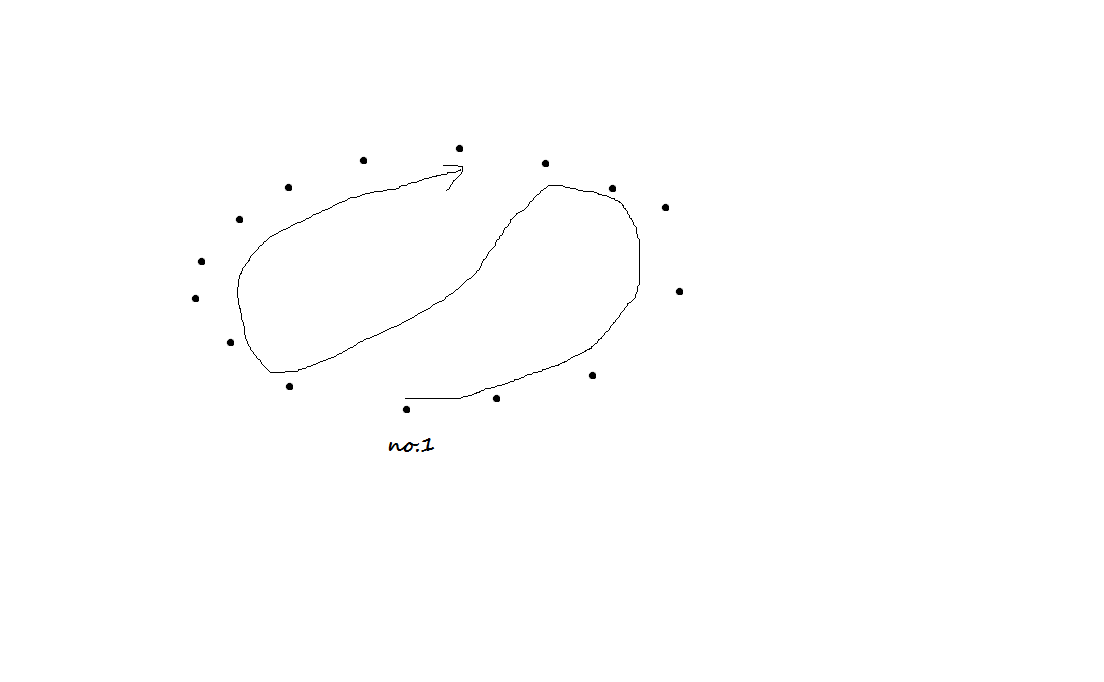
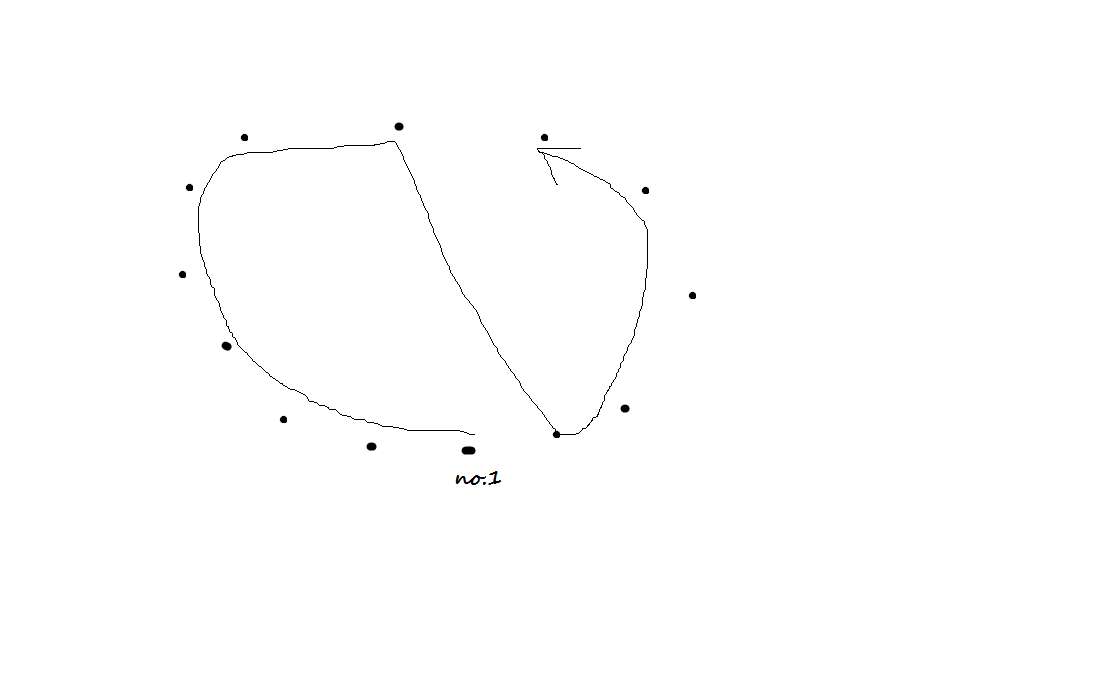
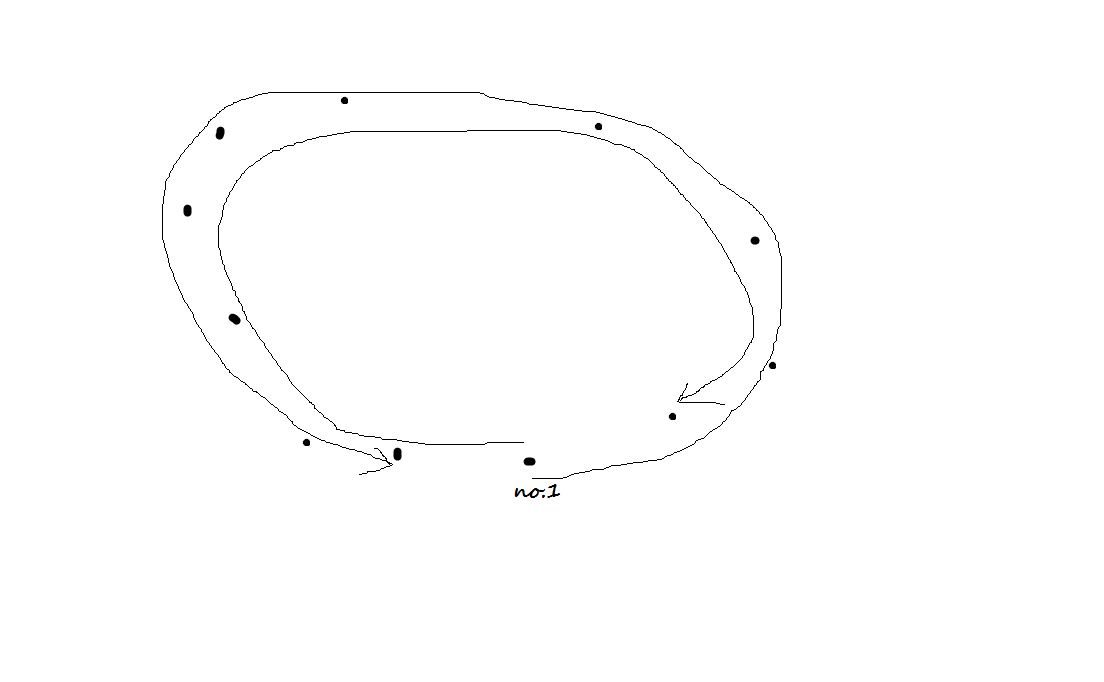
我们需要脑补一个贪心思路: 只有如图的 4 种遍历方式可能达到最优解:
所以我们可以提前算出从 1 号节点相邻的两个点分别顺时针和逆时针遍历到每个点的距离,就可以 O(n) 获得答案。但是这种方法只适用于凸多边形 (所以可以通过此题),凹多边形只能用动态规划,详见其他人的题解。本人无能写出那种高深的算法。
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <map>
#define MX 800
using namespace std;
typedef struct pot{double x,y;}pset;
pset p[MX];
int n;
double dist(pset a,pset b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
void cat()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%lf%lf",&p[i].x,&p[i].y);
}
double go1[MX][MX],go2[MX][MX];
void dog()
{
double dis1,dis2;
int i=1;
{
dis1=dis2=0;
for(int j=i+1;j<=i+n-2;j++)
{
dis1+=dist(p[(j-1)%n+1],p[(j+1-1)%n+1]);
go1[i][(j+1-1)%n+1]=dis1;
}
for(int j=i+n-1;j>=i+2;j--)
{
dis2+=dist(p[(j-1)%n+1],p[(j-1-1)%n+1]);
go2[i][(j-1-1)%n+1]=dis2;
}
}
}
void frog()
{
double mndis=9999999999;
int i=1;
for(int j=i+1;j<=i+n-2;j++)
mndis=min(0.0+dist(p[i],p[(i+1-1)%n+1])+go1[i][(j-1)%n+1]+dist(p[(j-1)%n+1],p[(i+n-1-1)%n+1])+go2[i][(j+1-1)%n+1],mndis);
for(int j=i+2;j<=i+n-1;j++)
mndis=min(0.0+dist(p[i],p[(i+n-1-1)%n+1])+go2[i][(j-1)%n+1]+dist(p[(j-1)%n+1],p[(i+1-1)%n+1])+go1[i][(j+n-1-1)%n+1],mndis);
printf("%.3lf\n",mndis);
}
int main()
{
freopen("frog.in","r",stdin);
freopen("frog.out","w",stdout);
cat();
dog();
frog();
return 0;
}
*
*
T2:security
题意:
给定一棵树,每个节点 i 可以花 wi 元安排守卫,守卫可以守护节点 i 和 i 的相邻节点。求守卫整棵树的最小花费。
思路:
多么水的一道树形 Dp, 而我却爆 0,原因很简单:没有开文件。否则这道题就是 100。说说思路:令 f[x][0] 表示 x 节点所在的子树中,x 节点安排守卫的最少花费;f[x][1] 表示 x 被自己的 一个或多个儿子看到的最少花费 ,f[x][2] 表示 x 被自己的爸爸看到的最少花费。
那么这里会有很多转移过程:(y∈x.son)
\begin{equation}
f[x][0]=min(\sum{f[y][0] or f[y][1] or f[y][2]})
\end{equation}
\begin{equation}
f[x][1]=min(\sum{f[y][0] or f[y][1]})
\end{equation}
\begin{equation}
f[x][2]=min(\sum{f[y][0] or f[y][1]})
\end{equation}
其中如果第二个转移中所有子树都选择了 f[y][1], 那么必须选出一个子树变为 f[y][0], 否则 x 节点就没有被任何一个子树看到。
然后我们只要确保了每个状态都正确转移就可以得到一个均摊复杂度 O(n) 的算法。
(你看头文件多美)
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#define MX 1000
#define oo 100000000090
using namespace std;
int fst[MX],nxt[MX*2],v[MX*2],w[MX];
int lnum,n;
void addeg(int nu,int nv)
{
lnum++;
nxt[lnum]=fst[nu];
fst[nu]=lnum;
v[lnum]=nv;
}
void input()
{
freopen("security.in","r",stdin);
freopen("security.out","w",stdout);
int t;
int a,b,c;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d%d%d",&a,&b,&c);
w[a]=b;
for(int j=1;j<=c;j++)
{
scanf("%d",&b);
addeg(a,b);
addeg(b,a);
}
}
}
long long f[MX][3];
void sch(int x,int fa)
{
f[x][0]=w[x];
f[x][1]=0;
f[x][2]=0;
int flg=0,t=0,fls=0;f[v[t]][0]=+oo; //flg 用于记录节点是否是叶子,fls 记录转移 2 中是否有一个子树看到了 x
for(int i=fst[x];i;i=nxt[i])
{
if(v[i]==fa)continue;
flg=1;
sch(v[i],x);
f[x][0]+=min(min(f[v[i]][0],f[v[i]][1]),f[v[i]][2]);
if(f[v[i]][0]-f[v[i]][1]<f[v[t]][0]-f[v[t]][1])t=i; //先找出转移 2 中如果要替换一棵子树,替换谁
f[x][2]+=min(f[v[i]][0],f[v[i]][1]);
}
for(int i=fst[x];i;i=nxt[i])if(v[i]!=fa)f[x][1]+=f[v[i]][1]; //先全部从 f[son][1] 转移
fls=0;
for(int i=fst[x];i;i=nxt[i]) //将 f[y][0] 更优的替换为 f[y][0]
if(v[i]!=fa&&f[v[i]][0]<f[v[i]][1])
f[x][1]+=f[v[i]][0]-f[v[i]][1],fls=1;
if(!fls)f[x][1]+=f[v[t]][0]-f[v[t]][1]; //如果没有一个替换为 f[y][0], 则强制替换之前找出的哪一个
if(flg==0)f[x][1]=+oo;
}
int main()
{
input();
sch(1,0);
cout<<min(f[1][0],f[1][1])<<endl;
return 0;
}
*
*
T3:LIS
题意:
求一个序列包含第 k 个元素的最长上升子序列
思路:
只需要把 k 之前的数列抠出来,把新数列中大于等于 a[k] 的元素删去,再把 k 之后的数列抠出来,删去小于等于 a[k] 的元素。分别对两个新序列做 O(nlogn) 的高速 LIS 结果相加再加一就是答案。
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#define MX 200000
using namespace std;
int src[MX+1],n,k;
int s1[MX+1],s2[MX+1],l1,l2;
int mp[MX*20+1];
int lis(int a[MX+1],int len)
{
int pos,mxpos=0;
memset(mp,0x4f,sizeof(mp));
for(int i=1;i<=len;i++)
{
pos=lower_bound(mp+1,mp+len+1,a[i])-mp;
mxpos=max(mxpos,pos);
mp[pos]=a[i];
}
return mxpos;
}
void input()
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)scanf("%d",&src[i]);
for(int i=1;i<k;i++)if(src[i]<src[k])s1[++l1]=src[i];
for(int i=k+1;i<=n;i++)if(src[i]>src[k])s2[++l2]=src[i];
}
int main()
{
freopen("lis.in","r",stdin);
freopen("lis.out","w",stdout);
input();
cout<<lis(s1,l1)+1+lis(s2,l2)<<endl;
return 0;
}
*
*
T4:palindrome(回文串)
题意:
给定一个字符串,求最少插入几个字母可以获得一个正规的回文串?
思路:
我唯一有把握 AC 的题,却因为开小了数组挂了 (fuck-fuck-fuck-shit)。
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#define MX 5005
using namespace std;
char str[MX];
int f[MX][MX],n;
int main()
{
freopen("palindrome.in","r",stdin);
freopen("palindrome.out","w",stdout);
scanf("%d",&n);
scanf("%s",str+1);
memset(f,0x4f,sizeof(f));
for(int i=1;i<=n;i++)f[i][0]=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j+i<=n;j++)
{
if(str[j]==str[j+i]&&i>=2)f[j][i]=min(f[j][i],f[j+1][i-2]);
if(str[j]==str[j+i]&&i==1)f[j][i]=0;
f[j][i]=min(f[j][i],min(f[j][i-1]+1,f[j+1][i-1]+1));
}
}
cout<<f[1][n-1]<<endl;
return 0;
}
0 条评论