课前预习
Q: 什么题目使用插头 dp?
A: 关键词:超小数据范围,网格图,连通性。
Q: 什么是 “插头”?
A: 一个格子通过某些方向与另一个格子相连,这些连接的位置叫做 “插头”。形象地理解,网格图上每一个格子是一块拼图,那么两块拼图的接口就叫做 “插头”。
Q: 什么是 “轮廓线”?
A: 我们在网格图中选择一个关键格子(图中黄色格子)$(i,j)$,轮廓线就是蓝色的线。
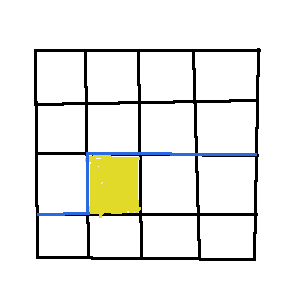
入门篇
题目大意: 一个网格图中有若干障碍格子,求其他格子的哈密尔顿回路总数
状态设计:
一看到巨小的数据范围,马上就可以想到状压。状压吼滴狠啊,那么怎么表示状态呢?
由于是哈密尔顿回路个数,所以人类的直觉告诉我们,状态一定和连通性相关。
对于每一单位轮廓线,如果没有插头与它相连,记为 0
假设轮廓线的单位部分从左到右记为 a,b,c,d,如果 a 和 c 连通,那么 b 和 d 不可能连通,这类似于括号匹配问题,所以我们还可以继续定义状态:
左括号插头记为 1,右括号插头记为 2,如图所示。
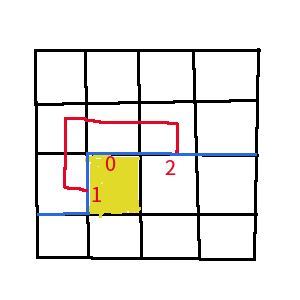
所以我们就得到了一个三进制的状态,又由于位运算是很快滴,所以我们使用 4 进制。
你可能会说,状态有可能巨多,或许时间和空间都承受不了?没关系,我们利用卓越的哈希技术,只保存当前轮廓线下可能存在的状态即可。
于是我们设计出了一个比较优秀的状态 $f(i,j,S)$,表示当前关键格子为 (i,j) 时,轮廓线状态为 $S$。
状态转移:
mp 是地图的意思。
每次转移,我们要把上图的蓝线转移成绿线,则首先提取箭头所指的两根线(取名为关键轮廓线)的状态,记为 $b_1$和 $b_2$。
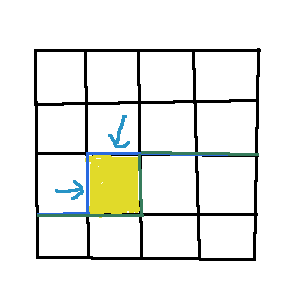
以下代码片中,ins(zt,num) 函数是将状态 zt 的方案数加上 num,mp 是地图,为 0 表示障碍,为 1 表示平地。$bin$是辅助我修改四进制下某一位的一个数组。如 $bin[j]$表示四进制下第 j 位。明白这些应该可以看懂代码片….. 吧?
1. 当前关键格子是一个障碍。
那么必须要两根关键轮廓线上都没有插头才合法,不改变轮廓线插头状态。
if(!mp[i][j]) {if(!b1&&!b2) ins(zt,num);}
2.b1=0 且 b2=0
那么只有可能如图设计关键格子里的线,就会增加一个左括号和一个右括号
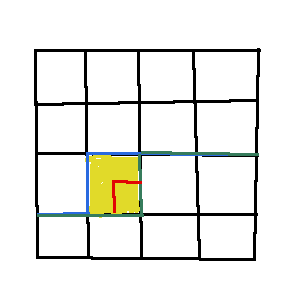
else if(!b1&&!b2)
{if(mp[i+1][j]&&mp[i][j+1]) ins(zt+bin[j-1]+2*bin[j],num);}
3.b1=0 或者 b2=0
b1=0 时,有两种连法,第一种如图,不改变括号状态
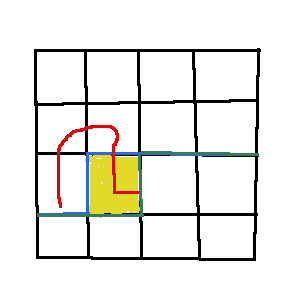
第二种相当于交换第 j 段轮廓线和第 j+1 段轮廓线的括号状态
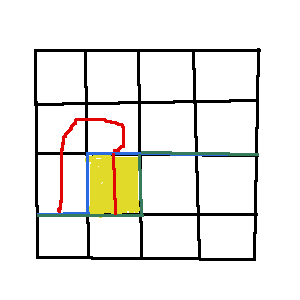
b2=0 时同理。
else if(!b1&&b2) {
if(mp[i][j+1]) ins(zt,num);
if(mp[i+1][j]) ins(zt-bin[j]*b2+bin[j-1]*b2,num);
}
else if(b1&&!b2) {
if(mp[i][j+1]) ins(zt-bin[j-1]*b1+bin[j]*b1,num);
if(mp[i+1][j]) ins(zt,num);
}
4.b1=b2
b1=b2=1 时,只能如图虚线连法,则第 j 段轮廓线和第 j-1 段状态都变成了 0,而原来这两段关键轮廓线对应的右括号状态发生了改变。所以 $O(n)$扫描去寻找右括号。
都等于 2 时同理,到前面去找左括号即可
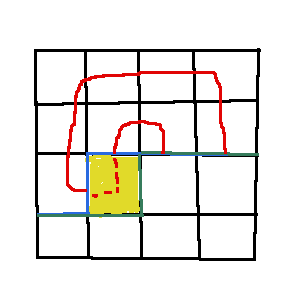
else if(b1==1&&b2==1) {
int kl=1;
for(int t=j+1;t<=m;++t) {
if((zt>>(t*2))%4==1) ++kl;
if((zt>>(t*2))%4==2) --kl;
if(!kl) {ins(zt-bin[j]-bin[j-1]-bin[t],num);break;}
}
}
else if(b1==2&&b2==2) {
int kl=1;
for(int t=j-2;t>=0;--t) {
if((zt>>(t*2))%4==1) --kl;
if((zt>>(t*2))%4==2) ++kl;
if(!kl) {ins(zt+bin[t]-2*bin[j]-2*bin[j-1],num);break;}
}
}
5.b1=2,b2=1
相当于去除了这两个括号,相信理解了前几种转移的你一定能自己画图吧~~(其实我懒得画了)~~
else if(b1==2&&b2==1) ins(zt-2*bin[j-1]-bin[j],num);
6.b1=1,b2=2
这可不得了,不能够盲目连起来,不然会出大问题的!会提前形成一个回路。
所以只有到达最后一个非障碍格子的时候,才能够连起来,并且得到最终一种合法方案了。
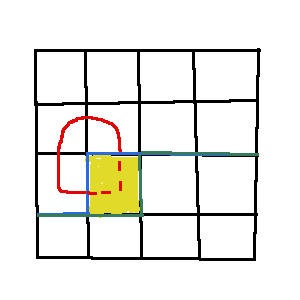
完整代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int LIM=300005,Has=299989;
int n,m,e1,e2,las,now,tt;LL ans;
int mp[15][15],bin[15],tot[2];LL js[2][LIM];
int h[300005],a[2][LIM],ne[LIM];
//tot: 状态总数,js: 该状态的方案总数,a: 各种状态
void ins(int zt,LL num) {//卓越的哈希技术
int tmp=zt%Has+1;
for(int i=h[tmp];i;i=ne[i])
if(a[now][i]==zt) {js[now][i]+=num;return;}
ne[++tot[now]]=h[tmp],h[tmp]=tot[now];
a[now][tot[now]]=zt,js[now][tot[now]]=num;
}
void work() {
tot[now]=1,js[now][1]=1,a[now][1]=0;
for(int i=1;i<=n;++i) {
for(int j=1;j<=tot[now];++j) a[now][j]<<=2;//切换行了
for(int j=1;j<=m;++j) {
las=now,now^=1;
memset(h,0,sizeof(h)),tot[now]=0;
for(int k=1;k<=tot[las];++k) {
int zt=a[las][k],b1=(zt>>(j*2-2))%4,b2=(zt>>(j*2))%4;//提取关键格子上的两段轮廓线状态
LL num=js[las][k];
if(!mp[i][j]) {if(!b1&&!b2) ins(zt,num);}
else if(!b1&&!b2)
{if(mp[i+1][j]&&mp[i][j+1]) ins(zt+bin[j-1]+2*bin[j],num);}
else if(!b1&&b2) {
if(mp[i][j+1]) ins(zt,num);
if(mp[i+1][j]) ins(zt-bin[j]*b2+bin[j-1]*b2,num);
}
else if(b1&&!b2) {
if(mp[i][j+1]) ins(zt-bin[j-1]*b1+bin[j]*b1,num);
if(mp[i+1][j]) ins(zt,num);
}
else if(b1==1&&b2==1) {
int kl=1;
for(int t=j+1;t<=m;++t) {
if((zt>>(t*2))%4==1) ++kl;
if((zt>>(t*2))%4==2) --kl;
if(!kl) {ins(zt-bin[j]-bin[j-1]-bin[t],num);break;}
}
}
else if(b1==2&&b2==2) {
int kl=1;
for(int t=j-2;t>=0;--t) {
if((zt>>(t*2))%4==1) --kl;
if((zt>>(t*2))%4==2) ++kl;
if(!kl) {ins(zt+bin[t]-2*bin[j]-2*bin[j-1],num);break;}
}
}
else if(b1==2&&b2==1) ins(zt-2*bin[j-1]-bin[j],num);
else if(i==e1&&j==e2) ans+=num;
}
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j) {
char ch=getchar();
while(ch!='*'&&ch!='.') ch=getchar();
if(ch=='.') mp[i][j]=1,e1=i,e2=j;
}
bin[0]=1;for(int i=1;i<=12;++i) bin[i]=bin[i-1]<<2;
work(),printf("%lld\n",ans);
return 0;
}
或许,你觉得上一题太难了(然蛾那是 CDQ 论文里的入门题),那么你可以先做一下这道题放松一下心情。
此题的回路数目不限,所以只需要记录有没有插头的状态,然后一顿瞎转移即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int n,m,T,kas,bin[15],mp[15][15];LL f[12][12][(1<<12)];
int main()
{
scanf("%d",&T);
bin[0]=1;for(int i=1;i<=12;++i) bin[i]=bin[i-1]<<1;
while(T--) {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j) scanf("%d",&mp[i][j]);
memset(f,0,sizeof(f));
f[0][m][0]=1;int lim=bin[m+1]-1;
for(int i=1;i<=n;++i) {
for(int zt=0;zt<=lim;++zt) f[i][0][zt<<1]=f[i-1][m][zt];
for(int j=1;j<=m;++j)
for(int zt=0;zt<=lim;++zt) {
int b1=zt&bin[j-1],b2=zt&bin[j];LL num=f[i][j-1][zt];
if(!mp[i][j]) {if(!b1&&!b2) f[i][j][zt]+=num;}
else if(!b1&&!b2)
{if(mp[i][j+1]&&mp[i+1][j])f[i][j][zt+bin[j-1]+bin[j]]+=num;}
else if(!b1&&b2) {
if(mp[i][j+1]) f[i][j][zt]+=num;
if(mp[i+1][j]) f[i][j][zt-bin[j]+bin[j-1]]+=num;
}
else if(b1&&!b2) {
if(mp[i][j+1]) f[i][j][zt-bin[j-1]+bin[j]]+=num;
if(mp[i+1][j]) f[i][j][zt]+=num;
}
else f[i][j][zt-bin[j-1]-bin[j]]+=num;
}
}
printf("Case %d: There are %lld ways to eat the trees.\n",++kas,f[n][m][0]);
}
return 0;
}
跳楼篇
GDKOI2016 Map 地图
题目大意: 有一张 $n \times m$的地图,有些地方是平地’.’,有些是障碍’#’,有些是未知的’?’,还有入口’S’,出口’E’ 和神器’X’。
合法的地图只有一个入口一个出口一个神器,并且入口,出口和神器两两连通。
现在要确定未知格子’?’ 是什么,问有多少种确定未知格子的方案使得地图合法?保证至少存在一种方案。
$1 \leq n \leq 7,1 \leq m \leq7$
题目解法:
我们可以保存轮廓线上格子的连通块编号(是障碍则为 0),由于题目友善,$n,m$小于等于 7,所以我们用 8 进制就好了。除了保存轮廓线上格子的连通块编号,还要保存入口,出口和神器的连通块编号(没出现过则为 0)。
假设现在在处理 $(x,y)$
对于问号格子,枚举它是什么,然后处理方式同下。
对于障碍,我们使得 y 列的连通块状态为 0。
对于非障碍,我们将 y-1 列和 y 列的连通块合并。
每次都要重编号。
然后用精妙的哈希技巧进行转移。
CDQ 的论文中说,有两种编码方式,一种是通过哈希,使用尽量小的号码。一种是连通块编号为在该连通块的最小纵坐标。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int mod=1000000007,Has=29987,LIM=300005;
int n,m,now,las,ans;
char mp[12][12],sp[5]={'S','X','E','.','#'};
int hav[3],tot[2],cod[12],hh[15];
LL a[2][LIM];int js[2][LIM],h[30005],ne[2][LIM];
int qm(int x) {return x>=mod?x-mod:x;}
void ins(LL zt,int num) {//精妙的哈希技巧
int tmp=zt%(LL)Has+1;
for(int i=h[tmp];i;i=ne[now][i])
if(a[now][i]==zt) {js[now][i]=qm(js[now][i]+num);return;}
ne[now][++tot[now]]=h[tmp],h[tmp]=tot[now];
a[now][tot[now]]=zt,js[now][tot[now]]=num;
}
void code(LL zt) {for(int i=1;i<=m+3;++i) cod[i]=(zt&7),zt>>=3;}//解码
LL bucode() {//重编码
memset(hh,-1,sizeof(hh));
hh[0]=0;int kl=0;LL re=0;
for(int i=m+3;i>=1;--i) {
if(hh[cod[i]]==-1) hh[cod[i]]=++kl;
re=(re<<3)|hh[cod[i]];
}
return re;
}
void hill(int x,int y) {//障碍
for(int i=1;i<=tot[las];++i)
code(a[las][i]),cod[y]=0,ins(bucode(),js[las][i]);
}
int check(int x,int y) {//检查是否可以放置特殊格
if(mp[x][y]=='S'&&cod[m+1]) return 1;
if(mp[x][y]=='X'&&cod[m+2]) return 1;
if(mp[x][y]=='E'&&cod[m+3]) return 1;
return 0;
}
void flat(int x,int y) {//非障碍
for(int i=1;i<=tot[las];++i) {
code(a[las][i]);if(check(x,y)) continue;
int b1=cod[y-1],b2=cod[y],b3=10;
if(b1) b3=min(b1,b3); if(b2) b3=min(b3,b2);
for(int j=1;j<=m+3;++j)
if((b1&&cod[j]==b1)||(b2&&cod[j]==b2)||(j==y)) cod[j]=b3;
if(mp[x][y]=='S') cod[m+1]=cod[y];
else if(mp[x][y]=='X') cod[m+2]=cod[y];
else if(mp[x][y]=='E') cod[m+3]=cod[y];
ins(bucode(),js[las][i]);
}
}
void work() {
tot[now]=1,js[now][1]=1,a[now][1]=0;
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j) {
las=now,now^=1,memset(h,0,sizeof(h)),tot[now]=0;
if(mp[i][j]!='?') {
if(mp[i][j]=='#') hill(i,j);
else flat(i,j);
}
else {
for(int t=0;t<=4;++t) {
if(t<=2&&hav[t]) continue;
mp[i][j]=sp[t];
if(mp[i][j]=='#') hill(i,j);
else flat(i,j);
}
}
}
for(int i=1;i<=tot[now];++i) {
code(a[now][i]);
if((!cod[m+1])||(!cod[m+2])||(!cod[m+3])) continue;
if(cod[m+1]==cod[m+2]&&cod[m+1]==cod[m+3]) ans=qm(ans+js[now][i]);
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i) {
scanf("%s",mp[i]+1);
for(int j=1;j<=m;++j)
if(mp[i][j]=='S') hav[0]=1;
else if(mp[i][j]=='X') hav[1]=1;
else if(mp[i][j]=='E') hav[2]=1;
}
work(),printf("%d\n",ans);
return 0;
}
为何跳楼:
我当时脑子抽筋,忽然想,“编号为在该连通块的最小纵坐标” 这中编号方式,似乎就不用每次转移都解码再重编码,好像简单一些。
然后挂在了障碍把特殊格子(入口出口或神器)与地图的其他部分隔开了的情况上。
然后我想,其实可以特判这种情况(不特判的话,就不能使用 8 进制了)。
然后又挂了。
很久很久过去了,我一怒之下重构代码,写了哈希最小编号法和每次转移都解码的写法。
还是挂的。
我就绝望了,在网上找了份标程对着看。
然后终于发现了错的地方:
if(cod[m+1]==cod[m+2]||cod[m+1]==cod[m+3]) ans=qm(ans+js[now][i]);
正确写法:
if(cod[m+1]==cod[m+2]&&cod[m+1]==cod[m+3]) ans=qm(ans+js[now][i]);
也就是说,我重构代码之前的那个代码,也是错的这个地方。
靠。
记录在此,引以为戒。
如果你现在还活着的话,我们来看:
最后一题
题目大意: 一个棋盘,若干格子已经被染成了黑或者白,染其他格子,使得所有黑格子在同一个连通块,所有白格子在同一连通块。并且不存在一个 $2 \times 2$的方格,其中所有格子颜色相同。求染色方案数并输出一种合法方案。
输出一种合法方案不难,对于每种 dp 状态记录任意一个可以转移到它的前状态和转移决策,然后递归输出即可。
那么此题,由于 $2 \times 2$方格那个限制,所以我们有必要记录当前格子 $(i,j)$左上方那个格子。然后由于要维护连通性,又和颜色有关,我们设计的状态应该包括连通性和颜色两个状态。别担心,由于颜色决定着连通性,所以总状态数并不会很多。
现在考虑状态的转移。无论黑白,连通状态的转移应该和当前格子及与它相邻的轮廓线上格子颜色是否一致,以下各条可以去 dp 函数中寻找对应代码写法。
1. 如果左边,上面,左上的格子和当前格子颜色相同,说明不合法。
2. 如果左上的格子和当前颜色相同,上面和左边的不同,且当前格子是最后一个格子的话,说明不合法
3. 如果上面的格子和当前格子颜色不同,并且整条轮廓线上存在和上面格子颜色相同却不在同一连通块的格子,则这两个连通块一定会被分隔开,不合法。如果不存在这样的格子的话,则剩下的所有格子都应该被染成和当前格子一样的颜色,如果当前格子不是 $(n,m-1)$或 $(n,m)$的话,一定会出现一个不满足条件的 $2 \times 2$方格,也不合法。综上两点,我们会发现,dp 完最后一个格子后,轮廓线上黑格子在同一连通块,白格子在同一连通块的方案,一定是合法方案。
4. 如果当前格子和上面格子颜色不同,和左边格子颜色相同,继承左边格子的连通块。如果和左边格子不同,和上面格子相同,继承上面格子的连通块。
5. 如果当前格子和左边与上面的格子颜色都不同,新建连通块
6. 如果和左边与上面颜色都相同,合并两个连通块
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int mod=1000000007,Has=299987,LIM=300005;
int T,n,m,now,las,bin[10];char mp[10][10];
int fa[80][LIM],cod[10],tt[12];char deis[80][LIM];//fa: 上一状态,deis: 决策
int a[2][LIM],h[LIM],c[2][LIM],ne[2][LIM],tot[2];LL js[2][LIM];
//a: 连通状态 c: 颜色状态,js: 方案数
void decode(int zt) {for(int i=0;i<m;++i) cod[i]=zt&7,zt>>=3;}//解码
int encode() {//最小表示法重编码
memset(tt,-1,sizeof(tt));
int kl=-1,re=0;
for(int i=m-1;i>=0;--i) {
if(tt[cod[i]]==-1) tt[cod[i]]=++kl;
re=(re<<3)|tt[cod[i]];
}
return re;
}
void ins(int sa,int sc,int id,int pre,LL num,char dd) {//精妙的哈希技巧
int tmp=sa%Has+1;
for(int i=h[tmp];i;i=ne[now][i])
if(c[now][i]==sc&&a[now][i]==sa) {js[now][i]+=num;return;}
++tot[now],a[now][tot[now]]=sa,c[now][tot[now]]=sc;
ne[now][tot[now]]=h[tmp],h[tmp]=tot[now],js[now][tot[now]]=num;
deis[id][tot[now]]=dd,fa[id][tot[now]]=pre;
}
void dp(int x,int y,int col) {
for(int i=1;i<=tot[las];++i) {
int zt=a[las][i],cc=c[las][i];
int cU=(x?((cc>>y)&1)==col:0),cL=(y?((cc>>(y-1))&1)==col:0);
int cUL= (cc>>m)==col;
if(cU&&cL&&cUL) continue;//1
if(!cU&&!cL&&cUL&&x==n-1&&y==m-1) continue;//2
decode(zt);
if(!cU&&x) {//3
int noc=0,inl=0;
for(int j=0;j<m;++j) {
if(((cc>>j)&1)!=col) ++noc;
if(cod[j]==cod[y]) ++inl;
}
if(inl==1&&noc>1) continue;
if(inl==1&&(x<n-1||y<m-2)) continue;
}
if(!cU&&cL) cod[y]=cod[y-1];//4
if(!cU&&!cL) cod[y]=m;//5
if(cU&&cL) {//6
int c1=cod[y],c2=cod[y-1];
for(int j=0;j<m;++j) if(cod[j]==c1) cod[j]=c2;
}
int coU=(cc&bin[y])?1:0,coUL=(cc&bin[m])?1:0;
cc=cc+bin[y]*(col-coU)+bin[m]*(coU-coUL);
ins(encode(),cc,x*m+y,i,js[las][i],(col?'#':'o'));
}
}
void print(int id) {//查找方案
for(int i=n-1;i>=0;--i)
for(int j=m-1;j>=0;--j) {
mp[i][j]=deis[i*m+j][id];
id=fa[i*m+j][id];
}
for(int i=0;i<n;++i) puts(mp[i]);
}
void work() {
now=0,tot[now]=1,c[now][1]=0,a[now][1]=0,js[now][1]=1;
for(int i=0;i<n;++i) {
for(int k=1;k<=tot[now];++k) c[now][k]-=c[now][k]&bin[m];
for(int j=0;j<m;++j) {
memset(h,0,sizeof(h)),las=now,now^=1,tot[now]=0;
if(mp[i][j]!='#') dp(i,j,0);
if(mp[i][j]!='o') dp(i,j,1);
}
}
LL ans=0;int id;
for(int i=1;i<=tot[now];++i) {
decode(a[now][i]);int kl=0;
for(int j=0;j<m;++j) kl=max(kl,cod[j]);
if(kl>1) continue;
ans+=js[now][i],id=i;
}
printf("%lld\n",ans);
if(ans) print(id);
}
int main()
{
scanf("%d",&T);
bin[0]=1;for(int i=1;i<=8;++i) bin[i]=bin[i-1]<<1;
while(T--) {
scanf("%d%d",&n,&m);
for(int i=0;i<n;++i) scanf("%s",mp[i]);
work(),puts("");
}
return 0;
}
0 条评论