并查集,顾名思义,就是把元素并到一个集合里,然后还可以查找某个元素在哪一个集合里;
这其实就是并查集了,思想很简单,而且很好写,不过很少会有题专门考并查集,但是,不可否认的是,并查集是一个极为有用的辅助算法,或者说是思想,再或者是一种实现方式;
并查集有几个主要操作:
Ⅰ 初始化:我们会把每一个点放入一个单独的集合,即 fa[x]=x,代表 x 所在的这个集合的代表元素是 x;
Ⅱ 查询:我们每一个集合的表现形式是一颗树,而所有的集合便表现为一个森林,所以我们递归地查询 x 所在的集合,一旦找到某一个点是一个集合的代表元素,那么我们就可以认为 x 与这个点在一个集合(而且一定在一个集合),并且这个集合是现在找到的这个点所代表的集合;
Ⅲ 合并: 假设我们希望把元素 A 与元素 B 合并到一个集合中,那么我们可以将这两个点所在的集合的代表元素合并到一个集合,至于这个过程,详情见代码;
声明:本博客图片来自网络;
查询:
int find(int x) //查找我(x)的掌门
{
int r=x; //委托 r 去找掌门
while (pre[r]!=r) //如果 r 的上级不是 r 自己(也就是说找到的大侠他不是掌门 = =)
r=pre[r] ; // r 就接着找他的上级,直到找到掌门为止。
return r ; //掌门驾到~~~
}
合并:
void join(int x,int y) //我想让虚竹和周芷若做朋友
{
int fx=find(x),fy=find(y); //虚竹的老大是玄慈,芷若 MM 的老大是灭绝
if(fx!=fy) //玄慈和灭绝显然不是同一个人
pre[fx]=fy; //方丈只好委委屈屈地当了师太的手下啦
}
还有一个路径压缩,比较重要,它一定程度上决定了并查集的效率;
所谓路径压缩,就是把原来是一个长链的树处理成一颗深度较浅的树,以至于查询时不至于递归太多次,其实就是一个小细节问题;
II find (R II x)
{
if(x==fa[x]) return x;
else return fa[x]=find(fa[x]);
//这个地方我们由 esle return find(fa[x]) 改为了
//return fa[x]=find(fa[x]);
//就是每次查询,我们就会把没有并在代表元素上的节点并到代表元素上;
//这样就可以使得树的深度较浅了;
}
效果大概就是这样的:
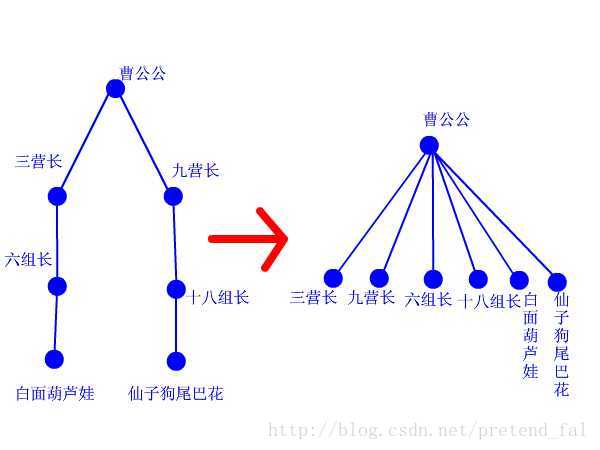
然后依旧是完整代码:
#include <bits/stdc++.h>
#define II int
#define IL inline
#define R register
#define I 123456
using namespace std;
IL void of(R II &a) {
R char c=getchar (); R II w=1, p=0;
while (c<'0'||c>'9') { if(c=='-') w=-1; c=getchar (); }
while (c>='0' && c<='9') { p=p*10+c-'0'; c=getchar (); }
a=w*p;
}
/* -------------------- Peipei -------------------- */
II fa[I];
II n,m;
II find (R II x)
{
if(x==fa[x]) return x;
else return fa[x]=find(fa[x]);
//这个地方我们由 esle return find(fa[x]) 改为了
//return fa[x]=find(fa[x]);
//就是每次查询,我们就会把没有并在代表元素上的节点并到代表元素上;
//这样就可以使得树的深度较浅了;
}
void join(R II x,R II y) { fa[x]=y; }
int main()
{
of(n); of(m);
for(R II i=1;i<=n;i++) fa[i]=i;
//初始化;
for(R II i=1,x,y,z;i<=m;i++)
{
of(x); of(y); of(z);
if(x==1) join(find(y),find(z));
//注意一定要传代表元素,保证正确性;
//不明白可以画图试一下;
else find(y)==find(z) ? printf("Y\n") : printf("N\n") ;
//查询是否在一个集合中;
}
return 0;
}
by pretend-fal;
END;
0 条评论