1. 题目
题意:
给出一个字符串,求它的长度除以它的最短循环节的长度的商。
有多组数据。
2. 题解
这题我们可以让字符串自己匹配自己找最短循环节。
但我用了一个定理:
一个字符存在循环节,当且仅当它的长度 $len$能被 $len-next[len]$整除,并且它的最短循环节就是下标在区间 $[1,len-next[len]]$内的它的子串(下标从 1 开始)
$next$指的是 kmp 中用到的那个 $next$数组。
其实本质和让字符串自己匹配自己是一样的。
我们稍微思考一下——
让字符串自己匹配自己,第一次匹配上一定是自己的前缀匹配到自己的后缀,如图所示:
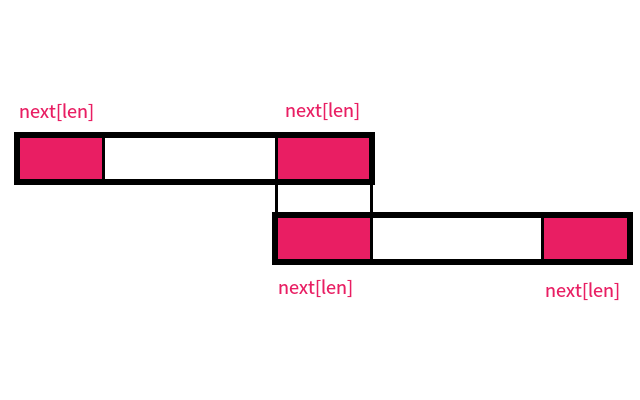
图中红色部分都是相同的子串。显然它们会最先被匹配到。
那么会出现这样的情况(为了好看我并没有和上图取相同情况):
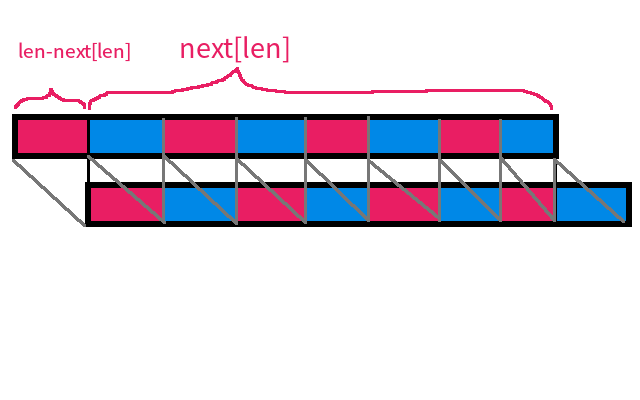
图中每个红色/蓝色部分都是一个循环节,每个循环节都是相等的。
注意图中灰色的斜线。因为上面那条的开头长度为 $len-next[len]$的那一段和下面那条开头长度为 $len-next[len]$的那段必然是相同的(因为上下两条是相同的字符串),而且上面那条的蓝色的第二段和下面那条红色的第一段是相同的(因为你进行了 kmp 匹配,中间长度为 $next[len]$的那一段上下两条都是相同的),所以上一条的第一段和第二段是相同的。
以此类推,就能发现开头长度为 $len-next[len]$的那一段是最短的循环节。
因此对于这题我们只要跑一遍 kmp 求出 next 数组再根据定理求出答案即可。
代码:
#include <cstdio>
#include <cstring>
#define NS (1000005)
using namespace std;
char str[NS];
int len, nxt[NS];
int main(int argc, char const* argv[])
{
while (scanf("%s", str), str[0] != '.')
{
len = strlen(str);
for (int i = 1, j = 0; i < len; i += 1)
{
while (j > 0 && str[i] != str[j]) j = nxt[j - 1];
if (str[i] == str[j]) j += 1;
nxt[i] = j;
}
if (len % (len - nxt[len - 1])) puts("1");
else printf("%d\n", len / (len - nxt[len - 1]));
}
return 0;
}
0 条评论