【算法】李超线段树

于由XZYQvQ发布

1. What’s this?

网上很多都是说。。。

线段树维护覆盖这个区间的” 最优势线段”，” 最优势线段” 指覆盖此区间且暴露最多的线段

我认为这。。。

是错的！

emmmm…

实际上李超线段树维护的是这个问题：

在线维护一个二维平面直角坐标系，支持插入线段，询问与直线 $x=x_0$相交的所有线段中交点纵坐标的最大（小）值

（顺带吐槽一下，网上那些代码都好奇怪的。。。什么插入线段分俩函数写，还有判断优势线段用求交点的方法。。。明明判断谁在 $mid$处取值大就行了嘛 OvO）

2. How it works

对于上面那个问题，用李超线段树维护 $x$轴。

我们为了方便描述，问题是询问最大值。

对于某个代表区间 $[l,r]$的线段树节点，保存在 $x$轴上的投影覆盖了区间 $[l,r]$的线段中与 $x=mid(mid=\frac{l+r}{2})$的交点纵坐标最大的线段。

比如下面这个：

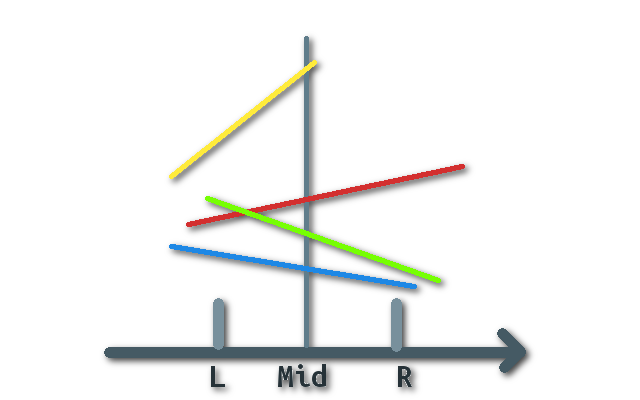
对于 $[l,r]$这个区间，我们应当保存的是红色线段。

而不是保存：

  • 黄色线段：因为黄色线段的投影并未覆盖区间 $[l,r]$
  • 绿色或蓝色线段：因为它们的交点纵坐标比红色的低

显然维护了这个东西的话上面那个问题的答案是可以知道的。

问题是怎么维护呢？显然我们不能暴力下传线段啊 OvO

当我们新加入一条线段的时候，有如下几种情况：

  1. 投影未覆盖当前节点代表区间 $[l,r]$（图中黄色线段），则继续向下递归到儿子节点
  2. 若投影覆盖了当前节点代表区间 $[l,r]$（红绿蓝线段）：
    1. 若节点未保存任何线段，则保存当前线段并 return
    2. 若保存了线段：
      1. 保存的线段在 $l$和 $r$处取值都比当前插入线段小（即保存线段在 $[l,r]$内取值都比当前线段小），则直接把保存线段替换成当前线段并 return
      2. 保存的线段在 $l$和 $r$处取值都比当前插入线段大，则直接 return
      3. 若在 $l$和 $r$处取值一小一大，则设在 $mid$处取值较大的为 $l_1$，取值较小的为 $l_2$。把当前节点的保存线段设为 $l_1$，然后下传处理 $l_2$：
        1. $l_1$斜率大于 $l_2$（如图中红色与绿色线段），则说明 $l_2$在 $[l,Mid]$内可以取到比 $l_1$更大的值，则把 $l_2$插入到左儿子 $[l,Mid]$中
        2. $l_1$斜率小于 $l_2$，则说明 $l2$在 $[Mid+1,r]$内可以取到比 $l1$更大的值，则把 $l_2$插入到右儿子 $[Mid+1,r]$中

这样处理了我们就能保证每个位置的最大取值可以在其线段树中的父亲节点（包括它自己）所保存的线段中取到。

查询的话用标记永久化的思想，一路查下来，取最大值即可。

大概就是（伪代码）：

double Query(int x)
{
    Node a = root; double res = -INF;
    while (a != NULL)
    {
        res = max(res, a.function(x));
        if (x <= a.mid) a = a.left_son;
        else a = a.right_son;
    }
    return res;
}

具体的代码可以看下面 QwQ

关于复杂度的话。。。

因为每次每条线段都会被减半，然后每条线段最多被下传 $log_2n$次，因此复杂度是 $O(nlog_2^2n)$的。

查询复杂度 $O(nlog_2n)$

3. Problems

T1. [Heoi2013]Segment BZOJ 3165

传送门=￣ω￣=

这题就是上面讲的那个问题。

不做过多赘述 OvO

有个小技巧：对于斜率不存在的线段（平行于 $y$轴），可以设其斜率为 $0$，设其与 $y$轴截距为 $max(y_0,y_1)$，这样就能像计算别的线段一样正常计算它的值了，不需要特判。

ps：目前这个代码没卡常就排在 BZOJ Rank 8，真是令我惊喜 OvO

代码：

#include <bits/stdc++.h>

#define DS (39989)
#define NS (100005)
#define LS(a) (a << 1)
#define RS(a) (a << 1 | 1)
#define eps (1e-6)

using namespace std;

template <typename _Tp> inline void IN(_Tp& dig)
{
    char c; bool flag = 0; dig = 0;
    while (c = getchar(), !isdigit(c)) if (c == '-') flag = 1;
    while (isdigit(c)) dig = dig * 10 + c - '0', c = getchar();
    if (flag) dig = -dig;
}

struct seg {double k, b;} l[NS];

int q, ans, cnt, e[(DS + 5) << 2];

double f(int a, int x)
{
    if (!a) return 0;
    return l[a].k * x + l[a].b;
}

void Insert(int x, int y, int d, int L, int R, int a)
{
    int Mid = (L + R) >> 1;
    if (x <= L && R <= y)
    {
        double dl = f(d, L), dr = f(d, R);
        double al = f(e[a], L), ar = f(e[a], R);
        if (dl <= al && dr <= ar) return;
        if (dl > al && dr > ar) {e[a] = d; return;}
        int l1, l2; double dm = f(d, Mid), am = f(e[a], Mid);
        if (abs(dm - am) < eps)
        {
            if (l[e[a]].k > l[d].k) l1 = e[a], l2 = d;
            else l1 = d, l2 = e[a];
        }
        else if (dm < am) l1 = e[a], l2 = d;
        else l1 = d, l2 = e[a];
        e[a] = l1;
        if (l[l1].k > l[l2].k) Insert(x, y, l2, L, Mid, LS(a));
        else Insert(x, y, l2, Mid + 1, R, RS(a));
        return;
    }
    if (x <= Mid) Insert(x, y, d, L, Mid, LS(a));
    if (y > Mid) Insert(x, y, d, Mid + 1, R, RS(a));
}

int Query(int x)
{
    int a = 1, L = 1, R = DS, Mid, res = 0;
    double mx = eps;
    while (L < R)
    {
        if (f(e[a], x) > mx) mx = f(e[a], x), res = e[a];
        if (Mid = (L + R) >> 1, x <= Mid) a = LS(a), R = Mid;
        else a = RS(a), L = Mid + 1;
    }
    if (f(e[a], x) > mx) res = e[a];
    return res;
}

int main(int argc, char const* argv[])
{
    IN(q); int o, x0, x1, y0, y1;
    while (q--)
    {
        IN(o);
        if (o)
        {
            IN(x0), IN(y0), IN(x1), IN(y1), cnt++;
            x0 = (x0 + ans - 1) % DS + 1, x1 = (x1 + ans - 1) % DS + 1;
            y0 = (y0 + ans - 1) % 1000000000 + 1;
            y1 = (y1 + ans - 1) % 1000000000 + 1;
            if (x0 > x1) swap(x0, x1), swap(y0, y1);
            if (x0 == x1) l[cnt].k = 0, l[cnt].b = max(y0, y1);
            else
            {
                l[cnt].k = (double)(y1 - y0) / (double)(x1 - x0);
                l[cnt].b = y0 - l[cnt].k * x0;
            }
            Insert(x0, x1, cnt, 1, DS, 1);
        }
        else IN(y0), y0 = (y0 + ans - 1) % DS + 1, printf("%d\n", ans = Query(y0));
    }
    return 0;
}

T2. [Sdoi2016] 游戏 BZOJ 4515

传送门=￣ω￣=

OvO

这里面是添加一个数字。。。是添加而不是加。。。

大概意思是每个节点是个桶，每次丢一个数字进去。。。

QwQ 直接说每个节点取最小不就行了！！！说成添加不是故意坑人吗！！！

因此这题就直接树剖+李超线段树就行了。。。

这里的李超线段树维护的下标是树剖的 Dfs 序，然后维护区间最小值即可。

复杂度是 $O(nlog_2^3n)$的。。。$n=10^5$。。。还跑的挺快。。。

代码：

#include <bits/stdc++.h>

#define NS (100005)
#define FS (123456789123456789ll)
#define LS(a) (a << 1)
#define RS(a) (a << 1 | 1)

using namespace std;

typedef long long LL;

template <typename _Tp> inline void IN(_Tp& dig)
{
    char c; bool flag = 0; dig = 0;
    while (c = getchar(), !isdigit(c)) if (c == '-') flag = 1;
    while (isdigit(c)) dig = dig * 10 + c - '0', c = getchar();
    if (flag) dig = -dig;
}

struct graph
{
    int head[NS], nxt[NS << 1], to[NS << 1], w[NS << 1], sz;
    void init() {memset(head, -1, sizeof(head)), sz = 0;}
    graph() {init();}
    void push(int a, int b, int c)
    {
        nxt[sz] = head[a], to[sz] = b, w[sz] = c, head[a] = sz++;
    }
    int operator [] (const int a) const {return to[a];}
} g;

int n, m, fa[NS], dep[NS], sz[NS], top[NS], id[NS], ps[NS], dfn, sc;

LL dis[NS];

struct edge
{
    LL k, b;
    LL f(int a)
    {
        return k * dis[a] + b;
    }
} s[NS << 1];

struct N {int l, r, d; LL mn;} e[NS << 2];

void Build(int l, int r, int a)
{
    e[a].l = l, e[a].r = r, e[a].mn = FS, e[a].d = 0;
    if (l == r) return; int Mid = (l + r) >> 1;
    Build(l, Mid, LS(a)), Build(Mid + 1, r, RS(a));
}

void szdfs(int a, int f)
{
    fa[a] = f, dep[a] = dep[f] + 1, sz[a] = 1;
    for (int i = g.head[a]; ~i; i = g.nxt[i])
        if (g[i] != f)
            dis[g[i]] = dis[a] + (LL)g.w[i], szdfs(g[i], a), sz[a] += sz[g[i]];
}

void dfs(int a)
{
    int mx = 0, mi = 0; id[a] = ++dfn, ps[dfn] = a;
    for (int i = g.head[a]; ~i; i = g.nxt[i])
        if (g[i] != fa[a] && sz[g[i]] > mx) mx = sz[g[i]], mi = g[i];
    if (!mi) return;
    top[mi] = top[a], dfs(mi);
    for (int i = g.head[a]; ~i; i = g.nxt[i])
        if (g[i] != fa[a] && g[i] != mi) top[g[i]] = g[i], dfs(g[i]);
}

void pup(int a)
{
    e[a].mn = min(e[LS(a)].mn, e[RS(a)].mn);
    e[a].mn = min(e[a].mn, min(s[e[a].d].f(ps[e[a].l]), s[e[a].d].f(ps[e[a].r])));
}

LL Query(int l, int r, int a)
{
    if (l <= e[a].l && e[a].r <= r) return e[a].mn;
    LL res = s[e[a].d].f(ps[max(l, e[a].l)]);
    res = min(res, s[e[a].d].f(ps[min(r, e[a].r)]));
    if (l <= e[LS(a)].r) res = min(res, Query(l, r, LS(a)));
    if (r >= e[RS(a)].l) res = min(res, Query(l, r, RS(a)));
    return res;
}

void Insert(int l, int r, int d, int a)
{
    if (l <= e[a].l && e[a].r <= r)
    {
        LL dl = s[d].f(ps[e[a].l]), dr = s[d].f(ps[e[a].r]);
        LL al = s[e[a].d].f(ps[e[a].l]), ar = s[e[a].d].f(ps[e[a].r]);
        if (al <= dl && ar <= dr) return;
        if (al > dl && ar > dr)
        {
            e[a].d = d, e[a].mn = min(e[a].mn, min(dl, dr));
            return;
        }
        LL dm = s[d].f(ps[e[LS(a)].r]), am = s[e[a].d].f(ps[e[LS(a)].r]);
        int l1 = e[a].d, l2 = d;
        if (dm <= am) swap(l1, l2), swap(al, dl), swap(ar, dr);
        e[a].d = l1;
        if (dl < al) Insert(l, r, l2, LS(a));
        else Insert(l, r, l2, RS(a));
        pup(a); return;
    }
    if (l <= e[LS(a)].r) Insert(l, r, d, LS(a));
    if (r >= e[RS(a)].l) Insert(l, r, d, RS(a));
    pup(a);
}

LL Work_Query(int a, int b)
{
    LL res = FS;
    while (top[a] != top[b])
    {
        if (dep[top[a]] > dep[top[b]]) swap(a, b);
        res = min(res, Query(id[top[b]], id[b], 1)), b = fa[top[b]];
    }
    if (dep[a] > dep[b]) swap(a, b);
    res = min(res, Query(id[a], id[b], 1)); return res;
}

int lca(int a, int b)
{
    while (top[a] != top[b])
    {
        if (dep[top[a]] > dep[top[b]]) swap(a, b);
        b = fa[top[b]];
    }
    if (dep[a] > dep[b]) swap(a, b);
    return a;
}

void Work_Insert(int u, int v, int a, int b)
{
    int lc = lca(u, v), flag = 0;
    s[++sc].k = -a, s[sc].b = dis[u] * a + b;
    s[++sc].k = a, s[sc].b = (dis[u] - 2 * dis[lc]) * a + b;
    while (top[u] != top[v])
    {
        if (dep[top[u]] > dep[top[v]]) swap(u, v), flag ^= 1;
        Insert(id[top[v]], id[v], sc - flag, 1), v = fa[top[v]];
    }
    if (dep[u] > dep[v]) swap(u, v), flag ^= 1;
    Insert(id[u], id[v], sc - flag, 1);
}

int main(int argc, char const* argv[])
{
    IN(n), IN(m), s[0].k = 0, s[0].b = FS;
    for (int i = 1, a, b, c; i < n; i += 1)
        IN(a), IN(b), IN(c), g.push(a, b, c), g.push(b, a, c);
    szdfs(1, 0), top[1] = 1, dfs(1), Build(1, n, 1);
    for (int i = 1, o, a, b, c, d; i <= m; i += 1)
    {
        IN(o), IN(a), IN(b);
        if (o == 2) printf("%lld\n", Work_Query(a, b));
        else IN(c), IN(d), Work_Insert(a, b, c, d);
    }
    return 0;
}
分类： 文章

XZYQvQ

炒鸡辣鸡的制杖蒟蒻一枚QvQ

0 条评论

发表回复

Avatar placeholder

您的电子邮箱地址不会被公开。 必填项已用 * 标注