话说好久没写文章了呢（QAQ 省选+APIO 完心态爆炸搞文化课去了，而且九月份还要去数竞比赛所以最近超忙的说 QwQ）
好了不多说了我们来进入今天的正题
先给一个可爱的题目链接酱
题意：给一个 $10^5$级别的序列，按照序列顺序生成一棵二叉查找树，求能够生成同样二叉查找树的所有序列中字典序最小的那个序列。
显然我们会知道生成一个二叉查找树后输出它的先序遍历就是最小的生成序列。
可是注意到二叉查找树这么 $naive$的东西是很容易退化的，最坏情况下能退化成链，使得构造这棵树的时间复杂度高达 $\Theta(n^2)$，这显然我们是接受不了的。
怎样加快建树时间呢？首先你需要有一个前置技能：笛卡尔树
那么笛卡尔树是什么呢？其实就是一棵满足二叉搜索树和堆性质的一棵普普通通的树家族中的一员啦（雾
因此它的中序遍历就是原序列（二叉搜索树的性质）
它的每一棵子树中最大 (小) 的 key 值都在根节点处（大 (小) 根堆的性质）
这里再补充一点，其实广义上来说你可以理解成每个点 i 上有两个值 $(a_i,b_i)$，其中 $a_i$满足二叉搜索树的性质，$b_i$满足堆的性质，特别地，若中序遍历是原序列的时候，那么 $a_i$所表示的就是这个点在原序列中的位置。
题目中原序列的 $a_i$值要满足二叉查找树的性质，那堆的性质呢？我们可以给序列中每一个数按顺序标号 $b_i$，则序列在生成树的时候，每个点（除根节点）的父亲的 $b_i$值肯定比它自己的 $b_i$值要小，满足小根堆的性质，因此我们可以用建笛卡尔树的方式把这棵树建起来了呢～，而且复杂度是可爱的 $\Theta(n^2)$
那怎么建笛卡尔树呢？
我们首先先考虑让它满足二叉查找树的性质，我们不妨先给 $a_i$排个序，让它成为这棵树的中序遍历，接着我们可以超级暴力地这样建：
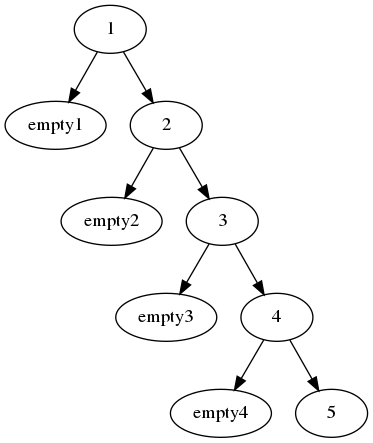
其中节点中数字代表该节点的 $a_i$值
(由于不太会用 dot 指定方向所以就画了几个空节点 QAQ)
可是这样建不一定符合堆的性质呀，所以我们采用一种策略：边建边调整
首先上述建法每次更新的点一定是在整棵树的最右边，因此新加入的点一定在最右边的那条链 (也就是根节点的右儿子的右儿子…)。并且最右边的那条链 $a_i$和 $b_i$的值都是单调递增的 (小根堆的性质)，因此我们可以每次找到最右链从上到下第一个 $b_i$值比当前要插入节点要大的点，把这个点丢到当前点的左儿子上，然后把当前点作为最右链的最下面的那个点即可。
再用伪代码表示一遍吧：
记 $now$表示当前插入的点，$big$表示最右链上第一个 $b_i$值比 $now$大的点。
tree[now].leftson = big;
fa[big].rightson = now;
我们可以用单调栈来维护最右链，因为每个点最多入栈出栈一次，于是我们就可以愉快地 $\Theta(n)$建树啦～
（排序的 nlogn：？？？）
恩所以这道题的复杂度是 $\Theta(nlogn + n)$
可爱的代码酱：
#include<bits/stdc++.h>
#define N 100005
#define ls s[0]
#define rs s[1]
#define fo(i, a, b) for (int i = (a); i <= (b); ++i)
struct node{
int x, y;//x 是 key 值 有二叉查找树性质 y 是插入顺序 有小根堆性质
friend inline bool operator < (node a, node b)
{
return a.x < b.x;
}
}a[N];
struct tree{
int s[2], x, y;
}t[N];
int n, sta[N], tot, last;
inline void print (int k)
{
if (!k) return;
printf("%d ", t[k].x);
print(t[k].ls);
print(t[k].rs);
}
int main ()
{
scanf("%d", &n);
fo (i, 1, n)
{
scanf("%d", &a[i].x);
a[i].y = i;
}
std::sort(a + 1, a + n + 1);
fo (i, 1, n)
{
int last = 0;
while (tot && t[sta[tot]].y > a[i].y)
last = tot--;
t[i].x = a[i].x; t[i].y = a[i].y;
t[i].ls = sta[last];
t[sta[tot]].rs = i;
sta[++tot] = i;
}
print(sta[1]);
}
0 条评论