1. 题面
题目描述
boshi 是 Rayment 的好朋友。
Rayment 最近迷上了一个叫 Just Shapes & Beats 的音游,于是就推荐给了 boshi(网易云上也有这个游戏部分音乐的歌单)。可 boshi 有点着迷于游戏音乐难以集中精神,有时反应慢了半拍,导致他在第二关就挂了一回。忍无可忍的 boshi 摘下了耳机,他决定用个更科学的方法来通过这一关。
这首歌的名字就叫做 Logic Gatekeeper,如果条件允许的话你也可以一边听歌一边切这道题目。
游戏的不同关卡攻击方式都不一样,但这关的攻击方式比较简单。形式化地来说,攻击可以被具象化为对一个矩阵的攻击,也就是说如果你待在这个矩阵的范围内,你就会受到 1 的攻击。
游戏界面可以认为是一个 n×m 的矩阵,而游戏角色恰好占一个方格的位置。boshi 会进行不断地进行预测某个子矩阵的攻击概率升高或降低了一定数值,同时为了评估某一个子矩阵的安全性,他也要知道如果他随机待在子矩阵内的一个位置,受到攻击的期望是多少。当然,初始时整个游戏界面任意一个位置的攻击概率为 0。
为了避免小数产生的误差,boshi 给出的所有的概率都是在模 $998244353$意义下的值,因此你在输出期望的时候也应该对 $998244353$取模。
Rayment 听得脑袋都晕了,boshi 只好请你来帮他过了这关,不受一点攻击才能拿到 S 评定。
输入格式
第一行三个整数 n,m,q,含义同题目描述。
接下来 q 行有两种格式,如下:
1 a b c d k,含义是以 (a,b) 为左下角,(c,d) 为右上角的子矩阵的攻击概率均加上 k2 a b c d,含义是询问以 (a,b) 为左下角,(c,d) 为右上角的子矩阵的攻击期望
输出格式
对于每一个 2 操作,输出一行一个整数,表示相应的答案。
样例输入
4 4 3
1 1 1 3 3 4
1 2 3 4 4 5
2 2 2 3 3
样例输出
499122183
数据范围与提示
样例解释:答案是 $\frac {26} 4$,模意义下即为 499122183。
$1\leq n,m\leq 10^6,1\leq q\leq 10^5$
$1\leq a\leq c\leq n,1\leq b\leq d\leq m,0\leq k<998244353$
评测时打开 O2 优化。没有 O2 优化也可以把时限开至 3s 的两倍。
友情链接:本首歌的网易云地址
2. 题解
Rayment 犇犇出的思考题
本意是让大家锻炼 CDQ 分治与卡常
但是本着我就是不用正解的智障杠精思想我还是没用正解
(所以请注意我这个大概比卡常的 CDQ+树状数组慢一倍)
(但是比 CDQ+线段树还是快多了)
首先可以看出这题就是《上帝造题的七分钟》的询问次数减少,空间放大版
因此不能用二位树状数组搞。
由此我陷入沉思——什么数据结构能离散地维护二维前缀和呢?
我甚至想自己发明一种数据结构。
最后想出了一种奇怪的,把空间分成三份的奇怪树
然后发现那个就是把两层合并成一层的 kd-tree…
于是我就打了 kd-tree
首先做法不做过多赘述了吧。。。
令 $A$为二维差分数组,即 $A _ {i,j}$表示 $(i,j)$到 $(n,m)$这个区域加上的值。
若是询问 $(1, 1)$到 $x, y$的矩阵的权值和,有:
$\sum _ {i=1} ^ x \sum _ {j=1} ^ y A _ {i, j} \times (x – i + 1) \times (y – j + 1)$
$=\sum _ {i=1} ^ x \sum _ {j=1} ^ y A _ {i,j} \times (xy + x + y + 1) – A _ {i, j} \times i (y + 1) – A _ {i, j} \times j (x + 1) + A _ {i, j} \times ij$
因此维护 $A _ {i, j},A _ {i, j} \times i, A _ {i, j} \times j, A _ {i, j} \times ij$即可
搞 4 棵 kd-tree 分别维护
单次询问二维前缀和的复杂度是 $O(log _ \frac 4 3 n)$的
怎么证明复杂度?
对于 kd-tree 的某个中心点(图中红色的那个点):
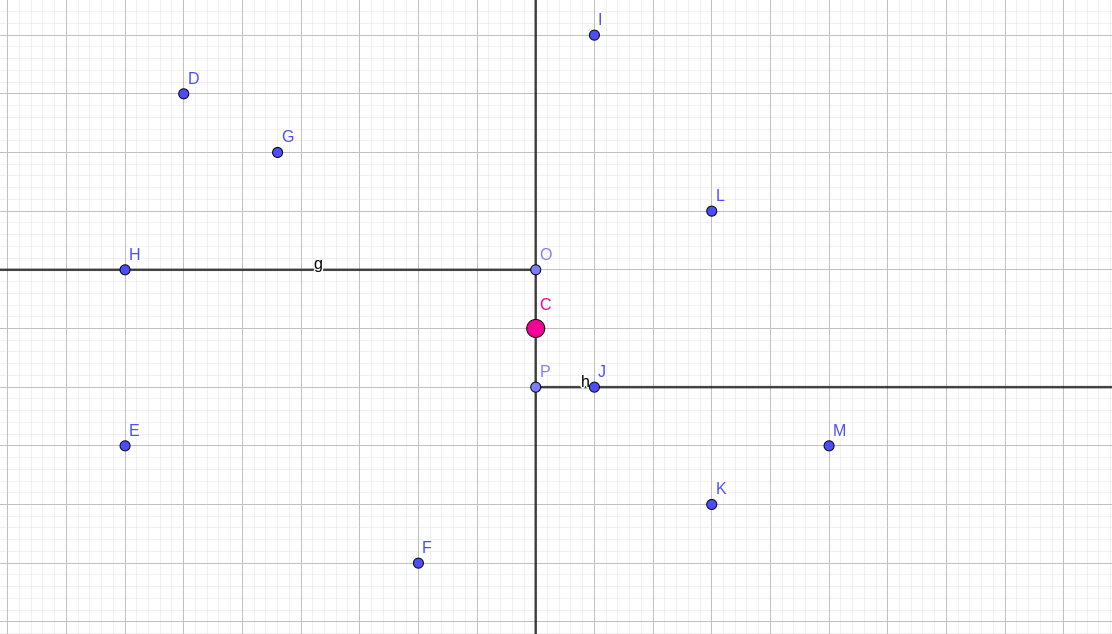
它和它左右俩儿子把平面分成了 4 个区域,每个区域的点数都是一样的。
- 如果询问(的右下角)落在了左上方的区域内,那么其他三个区域都可以舍去
- 如果询问落在了左下方,那么右边的两个区域都能舍去
- 如果询问落在了右上方,那么至少右下方的区域可以舍去
- 如果询问落在了右下方,那么左上方的整个区域都包含在了询问内,可以直接返回。
(这是左边的线高一些的情况,右边的线高一些的情况也是类似的)
这样至少每次能去掉 $\frac 1 4$的点,留下 $\frac 3 4$的点。
这样子一次的复杂度就是 $O(log _ {\frac 4 3}n)$的了
总复杂度是 $O(q log _ \frac 4 3 q)$的,理论复杂度比 $O(q log _ 2 ^2 q)$的要低
燃鹅。。。
如果你不做任何优化,在随机数据下你会发现你要跑大概 30 秒。。。
因为你不仅带了 kd-tree 的巨大常数,还带了整整一个 16 的大常数。。。
因此要卡常优化。。。
在这里提供这么几种优化方式:
- 保持树的平衡,类似替罪羊树的思想不断重构保证平衡,大概可以快一倍(如果数据不随机那么这一条是必须的)
- 还有一种更好的平衡方法,就是把操作离线,先把所有点都记录下来,最后一起建一颗 kd-tree,后面的插入操作改为修改操作,比上一种平衡方式快一倍
- 还有最关键的,四颗 kd-tree 的结构是完全相同的,只有值不同。我们没必要每次都重新寻找点的位置,我们可以把四颗树合并成一颗,每个节点开 4 个值域,每次查询返回 4 个值。。。这样可以弄到一个 $\frac 1 4$的常数!!!
然后还有 register 啊 inline 啊共用全局变量啊引用啊等等等等卡常。。。
然后我们就可以把最大数据要 1 分多钟的程序卡到 6 秒了。。。
燃鹅。。。燃鹅。。。
题目要求的是 3 秒。。。
那怎么办捏?
我是 OJ 管理员!!!233333~
于是我强行把实现开到 6 秒,就愉快地解决问题啦!(逃
(我真的卡不动了啊!!!T^T)
代码(讲真这代码我写了一遍又一遍,我觉得一共写的肯定已经上千行了。。。):
#pragma GCC optimize("Ofast,no-stack-protector")
#include <bits/stdc++.h>
#define NS (100005)
#define MOD (998244353)
#define REG register
using namespace std;
template <typename _Tp> inline void IN(_Tp& dig)
{
REG char c; REG bool flag = 0; dig = 0;
while (c = getchar(), !isdigit(c)) if (c == '-') flag = 1;
while (isdigit(c)) dig = dig * 10 + c - '0', c = getchar();
if (flag) dig = -dig;
}
inline int pls(REG int a, REG int b)
{
return a + b >= MOD ? a + b - MOD : a + b;
}
inline int mns(REG int a, REG int b) {return a - b < 0 ? a - b + MOD : a - b;}
inline int mul(REG int a, REG int b) {return 1ll * a * b % MOD;}
bool D;
struct N
{
int p[2], d[4], sum[4], mn[2], mx[2], s[2];
inline bool operator < (const N oth) const
{
if (p[D] == oth.p[D]) return p[D ^ 1] < oth.p[D ^ 1];
return p[D] < oth.p[D];
}
} arr[NS << 2];
struct Q {int x, y, d[4];};
struct kd_tree
{
int root, sz; N e[NS << 2]; Q o;
kd_tree()
{
root = sz = 0;
e[0].mn[0] = e[0].mn[1] = INT_MAX;
e[0].mx[0] = e[0].mx[1] = INT_MIN;
}
inline void pup(REG int a)
{
for (REG int i = 0; i < 4; i += 1)
e[a].sum[i] =
pls(e[a].d[i], pls(e[e[a].s[0]].sum[i], e[e[a].s[1]].sum[i]));
for (REG int i = 0; i < 2; i += 1)
{
e[a].mn[i] = min(e[a].p[i], min(e[e[a].s[0]].mn[i], e[e[a].s[1]].mn[i]));
e[a].mx[i] = max(e[a].p[i], max(e[e[a].s[0]].mx[i], e[e[a].s[1]].mx[i]));
}
}
inline void pup2(REG int a)
{
for (REG int i = 0; i < 4; i += 1)
e[a].sum[i] =
pls(e[a].d[i], pls(e[e[a].s[0]].sum[i], e[e[a].s[1]].sum[i]));
}
int build(REG int l, REG int r, REG bool dv)
{
if (l > r) return 0;
D = dv;
REG int a = ++sz, mid = (l + r) >> 1;
nth_element(arr + l, arr + mid, arr + r + 1);
e[a] = arr[mid];
e[a].s[0] = build(l, mid - 1, dv ^ 1);
e[a].s[1] = build(mid + 1, r, dv ^ 1);
pup(a); return a;
}
void modify(REG int a, REG bool dv)
{
if (e[a].p[0] == o.x && e[a].p[1] == o.y)
{
for (REG int i = 0; i < 4; i += 1) e[a].d[i] = pls(e[a].d[i], o.d[i]);
pup2(a); return;
}
if (!dv)
{
if (e[a].p[0] == o.x)
{
if (o.y < e[a].p[1]) modify(e[a].s[0], dv ^ 1);
else modify(e[a].s[1], dv ^ 1);
}
else
{
if (o.x < e[a].p[0]) modify(e[a].s[0], dv ^ 1);
else modify(e[a].s[1], dv ^ 1);
}
}
else
{
if (e[a].p[1] == o.y)
{
if (o.x < e[a].p[0]) modify(e[a].s[0], dv ^ 1);
else modify(e[a].s[1], dv ^ 1);
}
else
{
if (o.y < e[a].p[1]) modify(e[a].s[0], dv ^ 1);
else modify(e[a].s[1], dv ^ 1);
}
}
pup2(a);
}
inline void modify() {modify(root, 0);}
void query(REG int a)
{
if (!a || e[a].mn[0] > o.x || e[a].mn[1] > o.y) return;
if (e[a].mx[0] <= o.x && e[a].mx[1] <= o.y)
{
for (REG int i = 0; i < 4; i += 1) o.d[i] = pls(o.d[i], e[a].sum[i]);
return;
}
if (e[a].p[0] <= o.x && e[a].p[1] <= o.y)
for (REG int i = 0; i < 4; i += 1) o.d[i] = pls(o.d[i], e[a].d[i]);
query(e[a].s[0]), query(e[a].s[1]);
}
inline void query() {query(root);}
} kdt;
inline int qpow(REG int a, REG int b)
{
REG int res = 1; a %= MOD;
while (b)
{
if (b & 1) res = mul(res, a);
a = mul(a, a), b >>= 1;
}
return res % MOD;
}
inline int Inv(REG int a) {return qpow(a, MOD - 2);}
int n, m, q, o[NS], a[NS], b[NS], c[NS], d[NS], k[NS];;
int main(int argc, char const* argv[])
{
IN(n), IN(m), IN(q); REG int cnt = 0;
for (REG int i = 1; i <= q; i += 1)
{
IN(o[i]), IN(a[i]), IN(b[i]), IN(c[i]), IN(d[i]);
if (o[i] == 1)
{
IN(k[i]);
arr[++cnt].p[0] = a[i], arr[cnt].p[1] = b[i];
arr[++cnt].p[0] = c[i] + 1, arr[cnt].p[1] = d[i] + 1;
arr[++cnt].p[0] = a[i], arr[cnt].p[1] = d[i] + 1;
arr[++cnt].p[0] = c[i] + 1, arr[cnt].p[1] = b[i];
}
}
sort(arr + 1, arr + 1 + cnt); REG int tmp = cnt; cnt = 0;
for (REG int i = 1; i <= tmp; i += 1)
if (arr[i].p[0] != arr[i - 1].p[0] || arr[i].p[1] != arr[i - 1].p[1])
arr[++cnt] = arr[i];
kdt.root = kdt.build(1, cnt, 0);
for (REG int i = 1, res; i <= q; i += 1)
if (o[i] == 1)
{
kdt.o.x = a[i], kdt.o.y = b[i];
kdt.o.d[0] = k[i], kdt.o.d[1] = mul(a[i], k[i]);
kdt.o.d[2] = mul(b[i], k[i]), kdt.o.d[3] = mul(mul(a[i], b[i]), k[i]);
kdt.modify();
kdt.o.x = c[i] + 1, kdt.o.y = d[i] + 1;
kdt.o.d[0] = k[i], kdt.o.d[1] = mul(c[i] + 1, k[i]);
kdt.o.d[2] = mul(d[i] + 1, k[i]);
kdt.o.d[3] = mul(mul(c[i] + 1, d[i] + 1), k[i]);
kdt.modify();
kdt.o.x = a[i], kdt.o.y = d[i] + 1;
kdt.o.d[0] = mns(0, k[i]), kdt.o.d[1] = mns(0, mul(a[i], k[i]));
kdt.o.d[2] = mns(0, mul(d[i] + 1, k[i]));
kdt.o.d[3] = mns(0, mul(mul(a[i], d[i] + 1), k[i]));
kdt.modify();
kdt.o.x = c[i] + 1, kdt.o.y = b[i];
kdt.o.d[0] = mns(0, k[i]), kdt.o.d[1] = mns(0, mul(c[i] + 1, k[i]));
kdt.o.d[2] = mns(0, mul(b[i], k[i]));
kdt.o.d[3] = mns(0, mul(mul(c[i] + 1, b[i]), k[i]));
kdt.modify();
}
else
{
memset(kdt.o.d, 0, sizeof(kdt.o.d));
kdt.o.x = c[i], kdt.o.y = d[i], kdt.query();
res = pls(kdt.o.d[3],
mul(kdt.o.d[0], pls(pls(mul(c[i], d[i]), c[i]), d[i] + 1)));
res = mns(res, mul(kdt.o.d[1], d[i] + 1));
res = mns(res, mul(kdt.o.d[2], c[i] + 1));
memset(kdt.o.d, 0, sizeof(kdt.o.d));
kdt.o.x = a[i] - 1, kdt.o.y = b[i] - 1, kdt.query();
res = pls(res, kdt.o.d[3]);
res = pls(res,
mul(kdt.o.d[0], pls(pls(mul(a[i] - 1, b[i] - 1), a[i]), b[i] - 1)));
res = mns(res, mul(kdt.o.d[1], b[i]));
res = mns(res, mul(kdt.o.d[2], a[i]));
memset(kdt.o.d, 0, sizeof(kdt.o.d));
kdt.o.x = a[i] - 1, kdt.o.y = d[i], kdt.query();
res = mns(res, kdt.o.d[3]);
res = mns(res,
mul(kdt.o.d[0], pls(pls(mul(a[i] - 1, d[i]), a[i]), d[i])));
res = pls(res, mul(kdt.o.d[1], d[i] + 1));
res = pls(res, mul(kdt.o.d[2], a[i]));
memset(kdt.o.d, 0, sizeof(kdt.o.d));
kdt.o.x = c[i], kdt.o.y = b[i] - 1, kdt.query();
res = mns(res, kdt.o.d[3]);
res = mns(res,
mul(kdt.o.d[0], pls(pls(mul(c[i], b[i] - 1), c[i]), b[i])));
res = pls(res, mul(kdt.o.d[1], b[i]));
res = pls(res, mul(kdt.o.d[2], c[i] + 1));
printf("%d\n", mul(res, Inv(mul(c[i] - a[i] + 1, d[i] - b[i] + 1))));
}
return 0;
}
1 条评论
Remmina · 2020年3月9日 12:33 下午
事实证明当年我就是个傻子,当点非常密集时复杂度将会退化为 $O(\sqrt n)$