【算法】LCT 学习笔记 ——quhengyi11

于由HomuraCat发布

吐槽

这么简单的算法我为啥学会 $splay$之后等了好久才学 $QAQ$，大概 qhy 对码力要求高的算法总有一种抗拒心理，然而这个东西比后缀自动机好理解多了所以读者们请放心食用。

为了能更方便看懂我的代码，我在把我的代码中的宏定义放这里:

#define fo(i, a, b) for (int i = (a); i <= (b); ++i)
#define fd(i, a, b) for (int i = (a); i >= (b); --i)
#define N 300005
#define ls(u) t[u].s[0]
#define rs(u) t[u].s[1]

概念 (what’s LCT)

动态树 $LCT$(link cut tree) 是一个可以动态维护森林上各种信息的东西 (删除查找合并啥的都有吧)，原来的森林我们称为原森林，里面有实边和虚边，为啥有这两种边呢，首先 $LCT$是用很多个 splay 维护这个森林的信息，那么因为 splay 本来就是个二叉树，所以我们要将原森林” 剖分” 成很多个二叉树并且用 splay 来维护它，用实边连接起来的一棵树就是原森林中的一棵树，我们称它为原树。

这棵原树我们也不是直接用 splay 维护，而是按每个点在原树中的深度为优先级，将每个点以优先级的中序遍历丢到 splay 上。我们一般将原树所对应的 splay 称为辅助树，原森林就对应一个辅助树森林。

具体来讲大概就是，假设我们有一棵这样的原树：

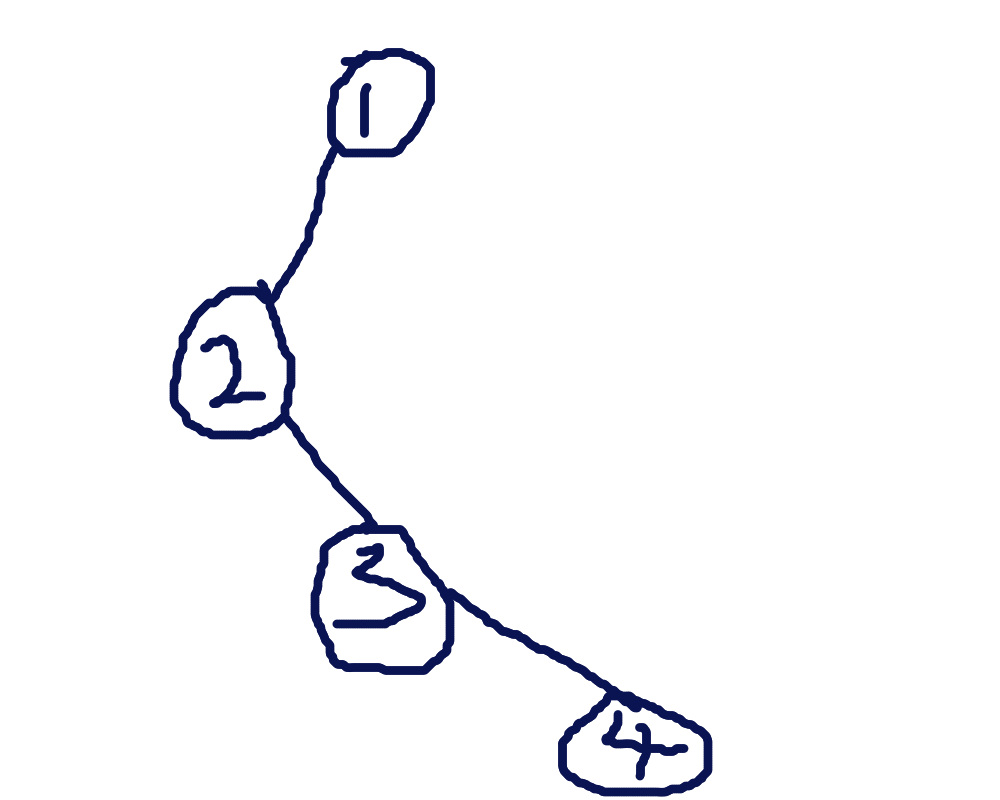
那么它的辅助树的其中一种可能情况就是这样子的:

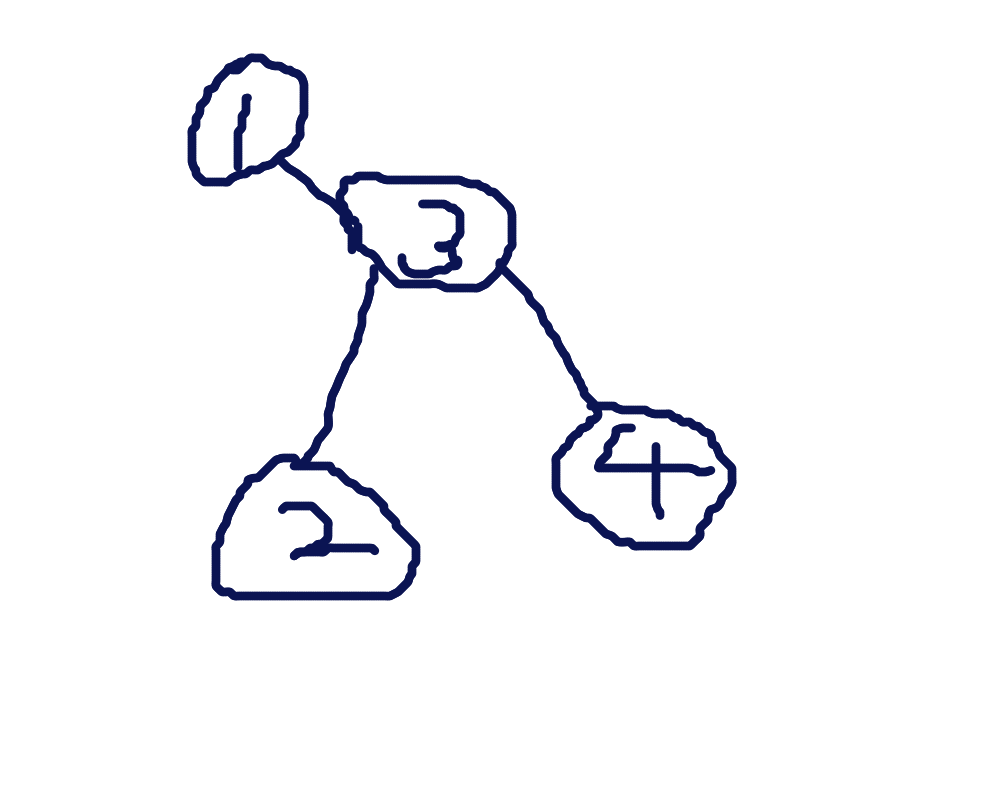
显然原树中同一个深度的点是不可能在一个 splay 里的，因此每个 splay 里面就是维护了原树中的一条链

LCT 的一些操作

access(u)

这个操作的意思是将点 $u$到原树中根节点 root 之间的链丢到一个辅助树 splay 里面

具体如何操作呢？

每次将 $u$点 splay 到当前所在辅助树的根节点，将它的右儿子更新为上一个 $u$，然后令 $u$跳到它的父节点，特别的，第一个 $u$的右儿子设为 $0$。

我们将 $u$旋转到辅助树的根节点，也就是将当前原树这条链上深度小于$u$(在 $u$上面的点) 丢到了 $u$的左子树上，将 $u$的右子树设为上一个 $u$点相当于将 $u$原来的右子树丢到了新的 splay 里面 (而它们之间用虚边相连)，并且将上一段链连接起来。

显然原树根的位置就是最后一个点 $u$的最左边的儿子

那么写成代码是酱紫的：

inline void access (int u)
{
    for (int las = 0; u; las = u, u = t[u].fa) 
        splay(u), rs(u) = las, update(u);
}

toroot(u)

这个操作的意思是将 $u$点变为原树的根节点

具体操作是我们先将 $u$点与原树中的根打通一条链，那么现在它们就在同一棵辅助树里面了，我们发现 $u$一定是在它所在的辅助树的中序遍历的最后一个的 (因为它是这条链上最深的点)，我们把 $u$点 splay 到辅助树的根上，那么 $u$显然是没有右子树的，我们要实现将 $u$移到原树的根上，也就是将 $u$到根的这条链的深度全部翻转一遍，在辅助树上的体现就是将整棵树翻转一遍，我们可以写个翻转标记来减少复杂度。

inline void toroot (int u)
{
    access(u); splay(u);
    std::swap(ls(u), rs(u));
    t[rs(u)].rev ^= 1;
}

findroot(u)

这个操作就是找到 $u$所在原树的根。
在 access 操作那里我也提到了，$u$的根就是 access 之后最左边的那个点，我们将 $u$点 splay 一下，找它的最左边的儿子就行，这里注意要下放标记，否则会找错它的根。

inline int findroot (int u)
{
    access(u); splay(u);
    while (ls(u)) {pushdown(u); u = ls(u);}
    return u;
}

link(u,v)

这个操作就是将 $u$和 $v$所在原树合并起来

首先将 $u$点丢到原树的根，然后去找找 $v$的根是不是 $u$，如果不是说明 $u,v$不在一个原树内，我们将 $u$的父节点设为 $v$，也就相当于从 $v$到 $u$连了一条虚边。

inline bool link (int u, int v)
{
    toroot(u);
    if (findroot(v) == u) return 0;
    t[u].fa = v;
    return 1;
}

split(u,v)

这个操作是将 $u$到 $v$之间的那条路径丢到一棵辅助树里，并且这棵辅助树以 $v$节点为根 (方便处理信息)。

这里如果你对 access 理解深刻你会很自然地想到这样做

先将 $u$丢到原树根节点，然后再将 $v$到根节点 access 打通一条路径，再将 $v$点 splay 上去就行。因为在打通路径的过程中 $u$已经不再是辅助树的根节点了，因为我们在 access 的过程中将 $v$到打通路径后的辅助树之间所有的原来的辅助树 (对应原树中的链) 都压成了一个点和一个左子树，那么 $v$到辅助树根节点的距离就会看起来比较少，所以这里我们选择将 $v$点 splay 上去而不是 $u$

inline void split (int u, int v) {toroot(u); access(v); splay(v);}

cut(u,v)

这个操作是将 $u,v$之间的那条边删掉，也就是将一棵原树分成两颗子树

首先我们先把 $u,v$之间的那条边用 $split(u,v)$拎出来，因为 $u,v$是相邻的，所 $v$的左儿子一定是 $u$，将它们的连边关系置为 0 就行。

因为 cut 太血腥太残暴了，因此我们将它写为 cat

update: 这里我第一次写的时候 cut 写假了，如果没有保证 cut 合法的情况下，应该如这个代码里面那样写，要注意！！！(模板题代码懒得改了)

具体表示 u 和 v 在一个原树里，并且 split 之后 u 是 v 的左儿子并且 u 的右儿子是空的（保证了中序遍历中 v 紧跟在 u 的后面，即深度相邻）

inline void cat (int u, int v)
{
    split(u, v);
    if (findroot(u) == findroot(v) && ls(v) == u && !rs(u))
    {
        t[u].fa = 0; ls(v) = 0;
        update(v);
    }
}

其它的一些操作

isroot(u)

判断 $u$是否为辅助树的根节点，如果是则返回 0，不是则返回 1

inline bool isroot (int u) {int fa = t[u].fa; return ls(fa) == u || rs(fa) == u;}

rotate(u)

这里需要注意一下，如果 $u$的父亲节点的父亲节点 $g$已经不在当前的这棵辅助树上，只需要连单向边 (也就是虚边，认父不认子)，否则正常连就行。

inline void con (int u, int v, int p) {t[v].fa = u; t[u].s[p] = v;}
inline void rotate (int u)
{
    int f = t[u].fa, g = t[f].fa, gs = pos(f), fs = pos(u);
    con(f, t[u].s[!fs], fs);
    if (isroot(f)) con(g, u, gs); else t[u].fa = g;
    con(u, f, !fs);
    update(f); update(u);
}

splay(u)

基础的 splay 操作想必各位都驾轻就熟了，同样要注意一下只能 splay 到辅助树的根节点，可以手动开栈来减少常数

inline void splay (int u)
{
    tot = 0;
    while (isroot(u)) S[++tot] = u, u = t[u].fa;
    S[++tot] = u;
    fd (i, tot, 1) pushdown(S[i]);
    u = S[1];
    for (; isroot(u); rotate(u))
        if (isroot(t[u].fa))
            rotate(pos(u) ^ pos(t[u].fa) ? u : t[u].fa);
}

模板题在这里

代码:

#include<bits/stdc++.h>
#define fo(i, a, b) for (int i = (a); i <= (b); ++i)
#define fd(i, a, b) for (int i = (a); i >= (b); --i)
#define N 300005
#define ls(u) t[u].s[0]
#define rs(u) t[u].s[1]
int data[N], n, root, q, m;
struct tree{
    int fa, s[2], sum;
    bool rev;
}t[N];
int S[N], tot;
inline bool isroot (int u) {int fa = t[u].fa; return ls(fa) == u || rs(fa) == u;}
inline bool pos (int u) {return rs(t[u].fa) == u;}
inline void con (int u, int v, int p) {t[v].fa = u; t[u].s[p] = v;}
inline void update (int u) {t[u].sum = t[ls(u)].sum ^ t[rs(u)].sum ^ data[u];}
inline void pushdown (int u)
{
    if (t[u].rev)
    {
        std::swap(ls(u), rs(u));
        t[ls(u)].rev ^= 1; t[rs(u)].rev ^= 1;
        t[u].rev = 0;
    }
}
inline void rotate (int u)
{
    int f = t[u].fa, g = t[f].fa, gs = pos(f), fs = pos(u);
    con(f, t[u].s[!fs], fs);
    if (isroot(f)) con(g, u, gs); else t[u].fa = g;
    con(u, f, !fs);
    update(f); update(u);
}
inline void splay (int u)
{
    tot = 0;
    while (isroot(u)) S[++tot] = u, u = t[u].fa;
    S[++tot] = u;
    fd (i, tot, 1) pushdown(S[i]);
    u = S[1];
    for (; isroot(u); rotate(u))
        if (isroot(t[u].fa))
            rotate(pos(u) ^ pos(t[u].fa) ? u : t[u].fa);
}
inline void access (int u)
{
    for (int las = 0; u; las = u, u = t[u].fa) 
        splay(u), rs(u) = las, update(u);
}
inline void toroot (int u)
{
    access(u); splay(u);
    std::swap(ls(u), rs(u));
    t[rs(u)].rev ^= 1;
}
inline void split (int u, int v) {toroot(u); access(v); splay(v);}
inline int findroot (int u)
{
    access(u); splay(u);
    while (ls(u)) {pushdown(u); u = ls(u);}
    return u;
}
inline bool link (int u, int v)
{
    toroot(u);
    if (findroot(v) == u) return 0;
    t[u].fa = v;
    return 1;
}
inline void cat (int u, int v)
{
    split(u, v);
    if (ls(v) == u)
    {
        t[u].fa = 0; ls(v) = 0;
        update(v);
    }
}
inline int query (int u, int v)
{
    split(u, v);
    return t[v].sum;
}
inline void modify (int u, int val)
{
    splay(u); data[u] = val; update(u);
}
int main ()
{
    scanf("%d %d", &n, &m);
    fo (i, 1, n) scanf("%d", &data[i]);
    fo (i, 1, m)
    {
        int opt, x, y;
        scanf("%d %d %d", &opt, &x, &y);
        if (!opt) printf("%d\n", query(x, y)); else
        if (opt == 1) link(x, y); else
        if (opt == 2) cat(x, y); else
        modify(x, y);
    }
    return 0;
}

讲真 LCT 可能只适合打省选暴力分

参考资料：

露迭月的学习笔记

flashhu 的学习笔记

Candy 学习笔记的第一句

后记：

没错我看了 Candy 的学习笔记第一句后有一种想把 lct 核心操作编到 Utopiosphere 歌词里面的冲动

Link, cut, access the chain.

Split your tree, rotate on splay.

一点都不押韵系列 XD

update: 附 snakes 新作

另外文章里如果有表达错误欢迎斧正 QAQ

分类： 文章

HomuraCat

明日は何になる? やがて君になる!

4 条评论

蒟蒻 · 2020年8月24日 7:26 下午

大佬，图挂了 qaq

回复

    蒟蒻 · 2020年8月24日 7:27 下午

    好吧，抱歉，　是电脑菜了

    回复

XZYQvQ · 2018年12月12日 10:46 下午

Orz TQL %%%%%

回复

    quhengyi11 · 2018年12月13日 5:46 下午

    qwq 您去年就会的算法我现在才写 QAQ(缩成一团.jpg)

    回复

发表回复

Avatar placeholder

您的电子邮箱地址不会被公开。 必填项已用 * 标注