//注:文章是 XZYQvQ 一个字一个字地码出来的,图也是一笔一笔画出来的,要转载一定要说明出处(https://www.mina.moe)啊/(ㄒoㄒ)/~~!
1. 一些废话
首先说明,本文中的指针都不是真正的指针,指的是数组下标的编号。
KMP 算法是一种改进的字符串匹配算法,由 D.E.Knuth,J.H.Morris 和 V.R.Pratt 同时发现,因此人们称它为克努特——莫里斯——普拉特操作(简称 KMP 算法)。KMP 算法的关键是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个 next() 函数,函数本身包含了模式串的局部匹配信息。时间复杂度 O(m+n)。
——度娘
其实这算法简称叫做看毛片算法
2. 基本思想
问题:从字符串 sup(长度为 n)中找到字符串 sub(长度为 m)。
朴素算法:枚举字符串 sub 的第一个字符对应的 sup 中的字符的编号,再挨个比较。复杂度 $O(n×m)$
kmp 算法:其他都与朴素算法相同,但是它改进了 “枚举字符串 sub 的第一个字符对应的 sup 中的字符的编号”这一过程,从而减小了复杂度。复杂度为 $O(n+m)$
那么 kmp 的基本思想到底是什么呢?
如图,我们要匹配字符串 sup、sub(在字符串 sup 里找 sub),其中蓝色的表示这段区域里面的字符都相等(匹配成功),粉色表示那个位置的字符不同:
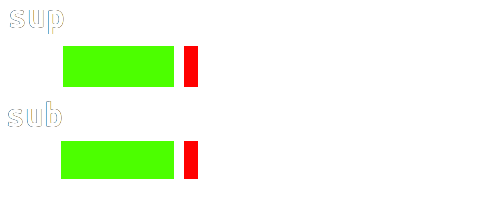
如果按照朴素的做法,这时候我们就应该把 sub 向右移动一位,再从头判断。
但我们 kmp 不会这样。它是怎么做的呢?
如图,假如这两块绿色区域内的字符串相同:
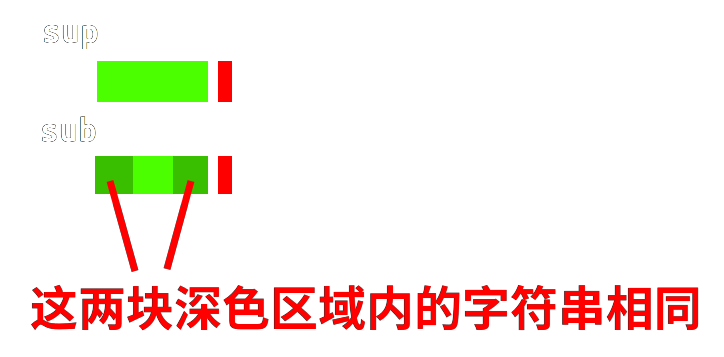
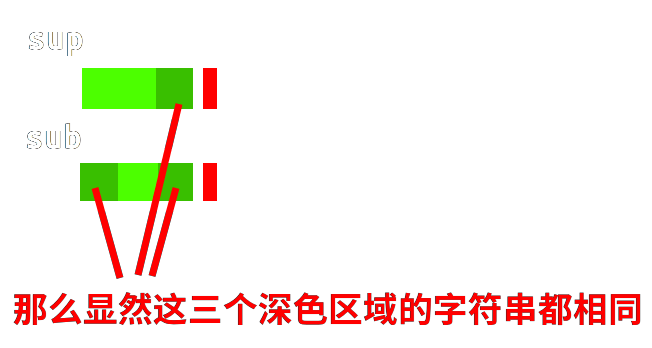
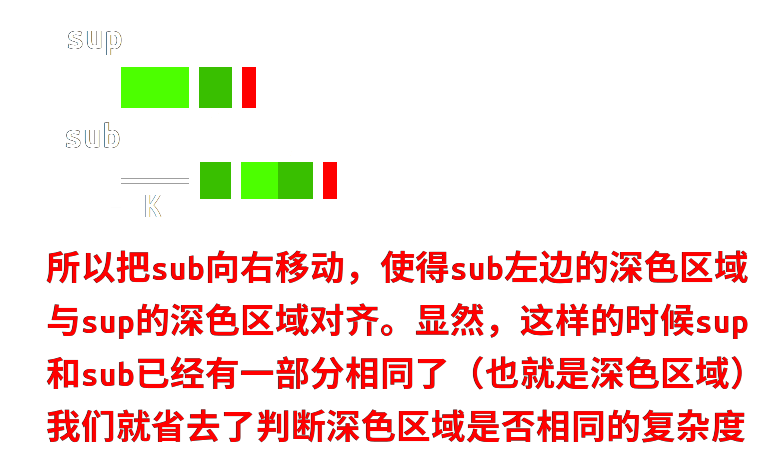
右移以后直接从对齐的绿色区域的后一位开始继续进行匹配判断。
这样就使得复杂度降低了。
根据势能分析可以得出复杂度是线性的,也就是 $O(n + m)$的。
3. 具体实现
移动字符串很简单:移动字符串其实就是移动指针。
那么我们怎么得到深色区域呢?
预处理。
设 $next[i]$表示在 sub 中,区间 $[0,i]$的最长的公共前缀后缀的长度(字符串的第一位下标为 0)。
什么是最长的公共前缀后缀的长度?
首先,前缀就是字符串的一个子串,子串的第一位是原字符串的第一位。
如原字符串为 abcdabcd,那它的前缀有:a,ab,abc,abcd,abcda,abcdab,abcdabc,abcdabcd。
后缀则反之。如原字符串依然为 abcdabcd,那么它的后缀有:d,cd,bcd,abcd,dabcd,cdabcd,bcdabcd,abcdabcd。
理解了这个,我们就能理解什么是最长的公共前缀后缀了。
它是一个字符串的前缀,同时也是该字符串的后缀。但它不能使字符串本身。
如 abcdabcd 中,最长的公共前缀后缀就是 abcd。
那它的最长的公共前缀后缀的长度就为 4。
所以,对于字符串 abcdabcd,它的 $next$数组是这样的:
$next[0]=0,next[1]=0,next[2]=0,next[3]=0,next[4]=1,next[5]=2,next[6]=3,next[7]=4$
所以当匹配到 sub 的第 i 为不同时,此时深色区域的长度就是 $next[i]$。
怎么得到 next 数组呢?
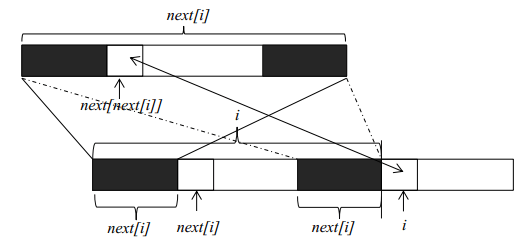
(图是网上找来的,出自:http://blog.csdn.net/yutianzuijin/article/details/11954939/)
我觉得有必要解释一下上面那个凌乱的图。
上面那一条 $next[i]$是下面那一条中两个黑色部分分别放大得到的(放大指的是图片放大!!!注意图中对应的实线、虚线、箭头的区别!!!)。
下面那条中左边的黑色部分和右边的黑色部分是相同的,所以放大后都是得到的上面那条。
它表示的是:下面那条中的黑色部分的最长公共前缀后缀的长度是 $next[next[i]]$!!!
假设我们现在已经求得 $next[0]$、$next[1]$、……$next[i-1]$,分别表示长度为 1 到 $i$的字符串的前缀和后缀最大公共长度,现在要求 $next[i]$。
由上图我们可以看到,如果位置 $i$和位置 $next[i-1]$处的两个字符相同,那么 $next[i]=next[i-1]+1$。
如果两个位置的字符不相同,我们可以将长度为 $next[i-1]$的字符串继续分割,获得其最大公共长度 $next[next[i-1]]$,然后再和位置 i 的字符比较。
这是因为长度为 $next[i-1]$前缀和后缀都可以分割成上部的构造,如果位置 $next[next[i-1]]$和位置 i 的字符相同,则 $next[i]=next[next[i-1]]+1$。
如果不相等,就可以继续分割长度为 $next[next[i-1]]$的字符串,直到字符串长度为 0 为止。
没看懂上面那个没关系,我也没看懂,鬼知道上面那几句话在扯什么。。。我从上面那个博客转载来的。。。
所以还是看代码吧
代码很简单,寥寥几行:
//这里 sub 的下标从 0 开始
for(int i=1,j=0;i<m;i++)//m 表示 sub 的长度,j 的值为 next[i-1],nxt 为 next 的缩写
{
while(j&&sub[i]!=sub[j])j=nxt[j-1];
//当 j!=0 且不符合条件时继续切割,至于为啥是 j-1 而不是 j 原因是下标是从 0 开始的
if(sub[i]==sub[j])j++;
//如果 sub[i]==sub[j] 则 next[i]++
nxt[i]=j;
}
实现了这个就很简单了。
在匹配字符串时,如果发现不匹配的字符就让指向 sub 的指针 $j$改变为 $next[j-1]$,直到 $j$为 0 或者位置 $j$的字符串匹配了。
为什么是 $j=next[j-1]$呢?
回到上面的图中,当前不匹配位(红色)的编号为 $j$,所以深色的区域的长度为 $next[j-1]$。
至于结束匹配:当指向 sup 的指针 $i$已经大于 $n$(sup 的长度)时,说明已经无法继续匹配了,匹配结束。
如果指向 sub 的指针 $j$已经大于 $m$(sub 的长度)时,说明新找到了一个匹配的字符串。
具体看代码吧。
下面的代码中我没用变量 $n, m$表示字符串长度。
$supl$表示字符串 sup 的长度,$subl$表示字符串 sub 的长度,$supi$表示 sup 的指针,$subi$表示 sub 的指针。
4. 例题&代码
都是模板题,思路我就不讲了。。。= ̄ω ̄=
1. 剪花布条 HDU – 2087
代码:
#include <bits/stdc++.h>
using namespace std;
char sup[1005],sub[1005];
int supl,subl,nxt[1005],supi,subi,ans;
int main()
{
while(scanf("%s",sup),strcmp(sup,"#")!=0)
{
scanf("%s",sub),supl=strlen(sup),subl=strlen(sub);
for(int i=1,j=0;i<subl;i++)
{
while(j&&sub[i]!=sub[j])j=nxt[j-1];
nxt[i]=j+=sub[i]==sub[j];
}
for(ans=supi=subi=0;supi<supl;supi++)
{
while(subi&&sup[supi]!=sub[subi])subi=nxt[subi-1];
subi+=sup[supi]==sub[subi];
if(subi==subl)ans++,subi=0;
}
printf("%d\n",ans);
}
return 0;
}
2. Oulipo HDU – 1686
代码:
#include <bits/stdc++.h>
using namespace std;
int t,supl,subl,supi,subi,nxt[10005],ans;
char sup[1000005],sub[10005];
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%s%s",sub,sup),subl=strlen(sub),supl=strlen(sup);
for(int i=1,j=0;i<subl;i++)
{
while(j&&sub[i]!=sub[j])j=nxt[j-1];
nxt[i]=j+=sub[i]==sub[j];
}
for(ans=subi=supi=0;supi<supl;supi++)
{
while(subi&&sup[supi]!=sub[subi])subi=nxt[subi-1];
subi+=sup[supi]==sub[subi];
if(subi==subl)ans++,subi=nxt[subi-1];
}
printf("%d\n",ans);
}
return 0;
}
3.【模板】KMP 字符串匹配 LUOGU – 3375
代码:
#include <bits/stdc++.h>
using namespace std;
int supl,subl,nxt[1005];
char sup[1000005],sub[1005];
int main()
{
scanf("%s%s",sup,sub),supl=strlen(sup),subl=strlen(sub);
for(int i=1,j=0;i<subl;i++)
{
while(j&&sub[i]!=sub[j])j=nxt[j-1];
nxt[i]=j+=sub[i]==sub[j];
}
for(int i=0,j=0;i<supl;i++)
{
while(j&&sup[i]!=sub[j])j=nxt[j-1];
j+=sup[i]==sub[j];
if(j==subl)printf("%d\n",i-j+2),j=nxt[j-1];
}
for(int i=0;i<subl;i++)printf("%d ",nxt[i]);
return 0;
}
4 条评论
[该用户已被删除] · 2018年12月16日 5:30 下午
我在看 dalao 一年半前写的文章 ||Σ( ° △ °|||)︴
XZYQvQ · 2018年12月16日 7:48 下午
一年半以前 XZY 乐呵呵
一年半以后 XZY 退役役
ZQC · 2018年7月13日 4:36 下午
%%%
XZYQvQ · 2018年7月13日 5:32 下午
emmmm….
您居然去雅礼了。。。