【算法】SPLAY 上手

于由BoringHacker发布

本文参考资料:

From yyb:Link

正文：关于 SPLAY

其实我更偏向于把 splay 叫做 cosplay

讲平衡树总逃不过 BST(Binary Search Tree)，二叉搜索树，以下是 BST 的性质：

一棵合法的 BST 每个节点上都带有一个数值，我们将其称为节点的 “关键码”。那么对于一棵 BST 上的任意节点，满足：

  • 该节点的关键码不小于它左子树的任意结点的关键码

  • 该结点的关键码不大于它右子树的任意结点的关键码

显然，BST 的中序遍历是一个递增的序列

建立一棵 BST

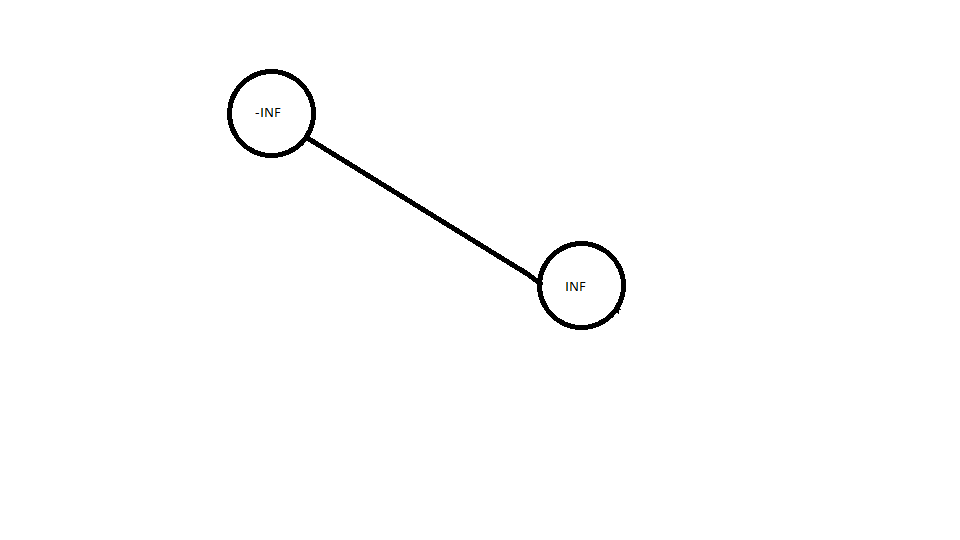
因为笔者很懒，不想到处判边界，所以我们一般可以在一棵空的 BST 中预先插入两个结点，一个正无穷，一个负无穷，如图:

img spfaed

const int SIZE = 1e5 + 5;
const int INF = 0x7fffffff;
struct BSTNode {
    int l, r; // 左右儿子的编号
   int val; // 关键码
} T[SIZE];
int tot, root;

int clone(int val) { // 新建节点
    T[++tot].val = val;
   return tot;
}

void build() {
    clone(-INF), clone(INF);
   root = 1, T[1].r = 2;
}

以上是建树的代码

那么，BST 就讲到这里

平衡树的诞生

当 BST 形成一条链的时候，每次查询会变成 $O(n^2)$

这种深度过深的 BST 是不平衡的。所以我们需要一种能保持树的深度在 $\log(n)$的数据结构，于是便诞生了平衡树

SPLAY

splay，又称 cosplay 伸展树，有 “序列之王” 的美称，常数巨大，跑的没有 $fhq-treap$快，但这不在我们的讨论范围以内

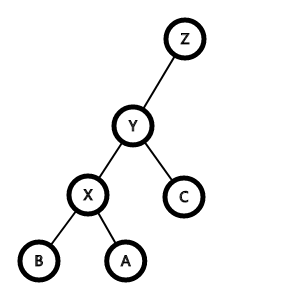
graph.png

想象一下这样一颗 BST，我们先把它们的大小关系列出来。

$$
Y<Z, C>Y, X<Y,A<X,B>X
$$

对于这样一颗 BST，我们可以通过一些特殊的方式来改变它的形态保持中序序列不变，这也是平衡树的精髓。

怎么改变呢？

旋转

旋转不转不是中国人，这是 splay 的精髓所在。

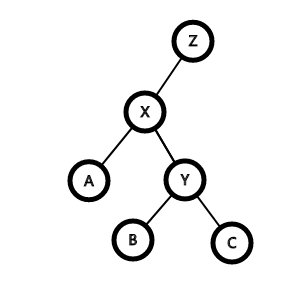
现在我们的目标是让 X 节点往上爬到它父亲节点 Y 处，让 Y 变成 X 的幺儿，也就是让 Y 节点下降。

这个过程首先要满足 BST 性质

通过例图来思考，此时的 X 节点是 Y 节点的左儿子，小于 Y 节点，为了不改变中序序列，我们可以让 Y 节点成为 X 的右儿子。那么问题来了：变换后的 Y 的确大于 X，但 X 还有一颗右子树呢！

别急，再回想一下 BST 的性质，任意节点大于其左子树中的任意节点，也就是说我们可以把 X 的左子树 B 拿给 Y 当左子树。

好了！世界核平了！Tarjan 放心了

展示一下旋转的成果吧！

旋转前：

graph.png

旋转后

graph _1_.png

别高兴得太早！

这只是一种情况，我们需要的是通用

这里有一个小技巧，即：

$$
odd\bigoplus1=odd-1
$$

$$
even\bigoplus1=even+1
$$

这个性质的证明很简单：

即得易见平凡，仿照上例显然。

留作习题答案略，读者自证不难。

反之亦然同理，推论自然成立，略去过程 QED，由上可知证毕。

$Just$ $a$ $joke$

设节点 Y 为 X 的父亲，Y 的 w(0 代表左儿子，1 代表右儿子) 儿子

  • $step1$: 将 Y 节点放到 X 节点的 w$\bigoplus$1 的位置
  • $step2$: 如果 X 的 w$\bigoplus$1 位置上有一颗子树，放在 Y 的 w 位置上
inline void update(int x) { // 更新节点信息
    T[x].siz = T[T[x].ch[0]].siz + T[T[x].ch[1]].siz + T[x].cnt;
}

inline void rotate(int x) { // 旋转
    int y = T[x].fa; // X 它爹
    int z = T[y].fa; // X 它爹它爹
    int w = T[y].ch[1] == x; // X 是它爹的左幺儿还是右幺儿
    T[z].ch[T[z].ch[1] == y] = x;
    T[x].fa = z;
    T[y].ch[w] = T[x].ch[w ^ 1];
    T[T[x].ch[w ^ 1]].fa = y;
    T[x].ch[w ^ 1] = y;
    T[y].fa = x;
    update(y), update(x);
}

仅仅有 rotate 操作还不够，splay 到目前为止依然很容易被卡。

想象这样一棵树：

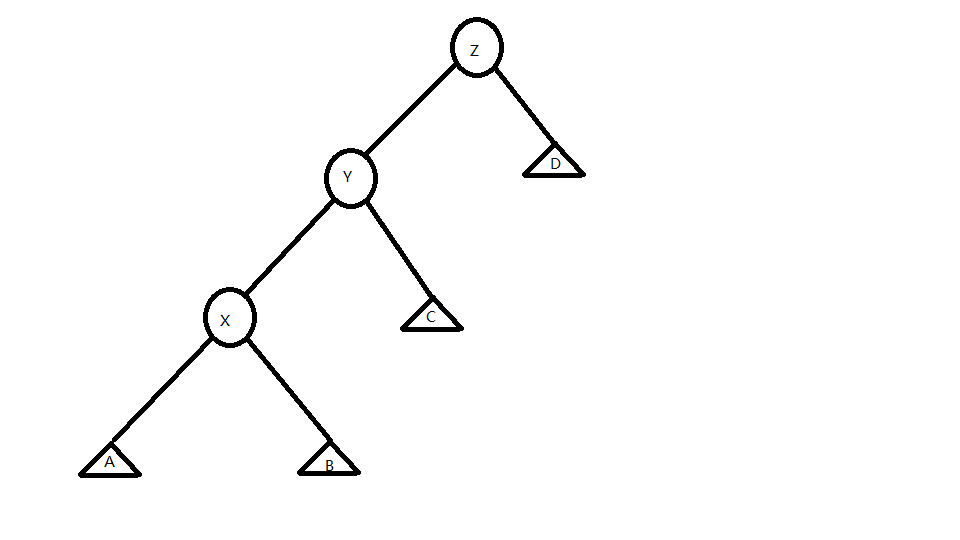
img spfaed

发现无论怎么旋转 X 都不能使得这棵树最长的一条链变短。我们称这种 X，X 它爹，X 它爹它爹在一条线上的情况称为三点共线。

怎么办呢？可怜的 splay 被人溜了

办法还是有滴

  • $step1$: 如果三点共线，我们可以先旋转 X 它爹，这样便可以使其更加 “平衡”
  • $step2$: 如果不共线……不共线……那就旋转 X 就好了

这便是 splay 操作

inline void splay(int x, int goal) { //splay
    for (; T[x].fa ^ goal; rotate(x)) { // 一直旋转到 x 成为 goal 的儿子
        int y = T[x].fa;
        int z = T[y].fa;
        if (z ^ goal)
            T[y].ch[1] ^ x ^ T[z].ch[1] ^ y ? rotate(x) : rotate(y); //判断三点是否共线，如果是，就旋转 Y，否则旋转 X
    }
    if (!goal) root = x; // 把根节点设为 X
}

至此，splay 就差不多讲完了，那么再来一道例题吧

【模板】普通平衡树

  • 题面：
您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：
1. 插入 x 数
2. 删除 x 数 (若有多个相同的数，因只删除一个)
3. 查询 x 数的排名 (排名定义为比当前数小的数的个数 +1 )
4. 查询排名为 x 的数
5. 求 x 的前驱 (前驱定义为小于 x，且最大的数)
6. 求 x 的后继 (后继定义为大于 x，且最小的数)

插入操作

首先我们先查找 BST 当中有没有和需要插入的节点关键码相同的节点，如果有，就把当前节点的 “副本” 数+1

如果没有，就遍历到叶子节点，再新增一个节点就好了

inline void insert(int x) {
    int u = root, fa = 0; // 从根节点开始找
    while (u && x ^ T[u].val) // 找关键码相同的节点
        fa = u, u = T[u].ch[x > T[u].val];
    if (u) T[u].cnt++; // 如果有，就增加一个副本
    else { // 否则新建一个节点
        u = ++tot;
        if (fa) T[fa].ch[x > T[fa].val] = u;
        T[u].fa = fa;
        T[u].siz = T[u].cnt = 1;
        T[u].ch[0] = T[u].ch[1] = 0;
        T[u].val = x;
    }
    splay(u, 0);
}

查找操作

设查找节点的关键码为 x，如果 x 大于当前节点的关键码，就往右子树跑，否则往左子树找。找到后把当前节点 splay 到根，保证 BST 的平衡

inline void find(int x) {
    int u = root;
    if (!u) return ; // BST 空
    while (T[u].ch[x > T[u].val] && x ^ T[u].val)
        u = T[u].ch[x > T[u].val];
    splay(u, 0);
}

前驱/后继操作

首先执行 find 操作。

以前驱为例，当前的根节点就是 x 的父节点，所以如果 root 的关键码大于 x，那么 root 就是 x 的前驱。否则就跳到左儿子找，再反着跳就好了

inline int next_bound(int x, int f) { // f=0 前驱，f=1 后继
    find(x);
    int u = root; // x 的父节点
    if (T[u].val > x && f) return u;
    if (T[u].val < x && !f) return u;
    u = T[u].ch[f]; // 跳到对应的子树
    while (T[u].ch[f ^ 1]) u = T[u].ch[f ^ 1]; // 反着跳转
    return u;
}

删除操作

找到这个数的 last，把他 splay 到根节点

然后找到这个数 next，把他 splay 到 last 的底下

然后……然后就没有了呀……

比 last 大是 next

比 next 小的且比 last 大的只有当前的节点

在 next 的左幺儿上面，

だから直接把 root 右幺儿的左幺儿删掉就可以了

inline void erase(int x) {
    int last = next_bound(x, 0);
    int next = next_bound(x, 1);
    splay(last, 0), splay(next, last);
    int del = T[next].ch[0];
    if (T[del].cnt > 1) {
        T[del].cnt--;
        splay(del, 0);
    }
    else T[next].ch[0] = 0;
}

第 K 大

现在再来看已经十分简单了

首先如果左子树的大小加上本身的个数大于 k，直接在左子树里找就行了

否则就把 k 减去左子树大小再减去本身的个数，再在右子树里找就行了

inline int kth_element(int x) {
    int u = root;
    if (T[u].siz < x) return 0; // 没有那么多，直接死亡
    while (233) {
        int y = T[u].ch[0];
        if (x > T[y].siz + T[u].cnt) {
            x -= T[y].siz + T[u].cnt;
            u = T[u].ch[1];
        }
        else if (T[y].siz >= x) u = y;
        else return T[u].val;
    }
}

完整代码：

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>

using namespace std;

const int SIZE = 1e5 + 5;
int n, root, tot;
struct SPLAY {
    int fa;
    int siz;
    int cnt;
    int val;
    int ch[2];
} T[SIZE];

inline void update(int x) {
    T[x].siz = T[T[x].ch[0]].siz + T[T[x].ch[1]].siz + T[x].cnt;
}

inline void rotate(int x) {
    int y = T[x].fa;
    int z = T[y].fa;
    int w = T[y].ch[1] == x;
    T[z].ch[T[z].ch[1] == y] = x;
    T[x].fa = z;
    T[y].ch[w] = T[x].ch[w ^ 1];
    T[T[x].ch[w ^ 1]].fa = y;
    T[x].ch[w ^ 1] = y;
    T[y].fa = x;
    update(y), update(x);
}

inline void splay(int x, int goal) {
    for (; T[x].fa ^ goal; rotate(x)) {
        int y = T[x].fa;
        int z = T[y].fa;
        if (z ^ goal)
            T[y].ch[1] ^ x ^ T[z].ch[1] ^ y ? rotate(x) : rotate(y);
    }
    if (!goal) root = x;
}

inline void find(int x) {
    int u = root;
    if (!u) return ;
    while (T[u].ch[x > T[u].val] && x ^ T[u].val)
        u = T[u].ch[x > T[u].val];
    splay(u, 0);
}

inline void insert(int x) {
    int u = root, fa = 0;
    while (u && x ^ T[u].val)
        fa = u, u = T[u].ch[x > T[u].val];
    if (u) T[u].cnt++;
    else {
        u = ++tot;
        if (fa) T[fa].ch[x > T[fa].val] = u;
        T[u].fa = fa;
        T[u].siz = T[u].cnt = 1;
        T[u].ch[0] = T[u].ch[1] = 0;
        T[u].val = x;
    }
    splay(u, 0);
}

inline int next_bound(int x, int f) {
    find(x);
    int u = root;
    if (T[u].val > x && f) return u;
    if (T[u].val < x && !f) return u;
    u = T[u].ch[f];
    while (T[u].ch[f ^ 1]) u = T[u].ch[f ^ 1];
    return u;
}

inline void erase(int x) {
    int last = next_bound(x, 0);
    int next = next_bound(x, 1);
    splay(last, 0), splay(next, last);
    int del = T[next].ch[0];
    if (T[del].cnt > 1) {
        T[del].cnt--;
        splay(del, 0);
    }
    else T[next].ch[0] = 0;
}

inline int kth_element(int x) {
    int u = root;
    if (T[u].siz < x) return 0;
    while (233) {
        int y = T[u].ch[0];
        if (x > T[y].siz + T[u].cnt) {
            x -= T[y].siz + T[u].cnt;
            u = T[u].ch[1];
        }
        else if (T[y].siz >= x) u = y;
        else return T[u].val;
    }
}

signed main() {
    scanf("%d", &n);
    insert(1e9);
    insert(-1e9);
    for (int i = 1; i <= n; ++i) {
        int opt, x;
        scanf("%d %d", &opt, &x);
        if (opt == 1) insert(x);
        if (opt == 2) erase(x);
        if (opt == 3) {
            find(x);
            printf("%d\n", T[T[root].ch[0]].siz);
        }
        if (opt == 4) printf("%d\n", kth_element(x + 1));
        if (opt == 5) printf("%d\n", T[next_bound(x, 0)].val);
        if (opt == 6) printf("%d\n", T[next_bound(x, 1)].val);
    }
    return 0;
}
分类： 文章

3 条评论

ljx · 2020年1月20日 10:14 下午

与前驱后继时特判同理

回复

ljx · 2020年1月20日 10:13 下午

opt=3 时，应该要特判根节点的值是否小于 x

回复

Remmina · 2019年12月19日 11:14 下午

很抱歉咕了您这么久，主要是最近马上期末考试了站长同学真没啥时间去审核，而 Qiuly 同学可能也有些事吧 QAQ
非常抱歉 Orz
另外感谢您投稿的优质文章！(*￣︶￣)

回复

发表回复

Avatar placeholder

您的电子邮箱地址不会被公开。 必填项已用 * 标注