很妙的一道计数题
思路
首先可以明确如果枚举每种连边情况 暴力计算连通块时间复杂度是不可接受的
(题目中%1e9+7 不就表明了这一点)
因此考虑计算每一种连通块的总出现次数 即对答案的贡献
(“因此” 好难想)
性质:
- 如果设 $(l1,r1)$,$(l2,r2)$分别为两条连边且 $l1<r1$,$l2<r2$
若 $l1<=l2<r2<=r2$则两条直线必不相交 $l1<r1<=l1<=r2$时也必不相交
那么仅有交叉关系时相交 因此 给定一条线段的两个端点 我们能判定他们的相交关系
- 我们来分析连通块
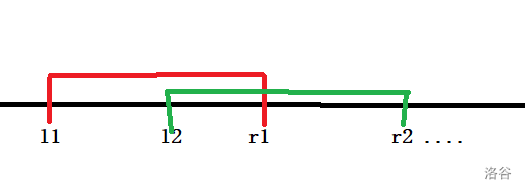
此时 $l1,l2,r1,r2$同属一个连通块

此时 $l1,l2,r1,r2$同属一个连通块而 $l3,r3$属于另一个连通块
同时两个连通块不同当且仅当至少有一个点出现在其中一块中而不存在另一块中
因此一个连通块最左的点和最右的点可以表示一个连通块
用人话说就是
令 $l1,r1$为连通块 A 最左侧和右侧的点;
$l2,r2$为连通块 B 最左侧和右侧的点
若 $l1\neq l2$或 $r1 \neq r2$则连通块 $A\neq B$
从性质出发的做法
令 $f_{i,j} $表示以 $i,j$为左右端点的连通块的贡献次数
显然只要区间 $(i,j)$里头的东西不要往区间外连 那么随意连都是合法的
令 $cnt_{i,j}$表示 $(i,j)$里还有多少点可以随意连
$g_i$表示 $i$个点的连线总方案
即有 $f_{i,j} $=$g_{cnt_{i,j}}-∑f_{i,k}*g_{cnt_{k+1,j}}$
然后 $O(n^3)$搞定(
3 条评论
Qiuly · 2021年10月31日 8:34 下午
图是不是挂了 /kk
Hencecho · 2021年11月2日 3:28 下午
好像是的()
洛谷图床容易出锅/kk
Qiuly · 2021年11月9日 6:55 下午
还是看不了 /kk