前言

litble 不会 FFT 和 NTT，是自己太蒻了。
学习数学知识需要耐心，所以也请和蒟蒻 litble 一样站在门外的人保持耐心来学，加油吧！
另外，litble 很好奇，为什么《数学一本通》讲这些东西只讲了半页纸。

复数

参考博客，同时借了张图。

复数的基本定义

虚数单位:$i=\sqrt {-1}$
对于一个数轴上的实数 a，让 a×(-1) 得到-a，那么 a 就在数轴上旋转了 180°。也就是说，a×i×i 相当于把 a 旋转 180°，a×i 就是把 a 旋转 90°。于是我们就得到了一个美丽的平面：

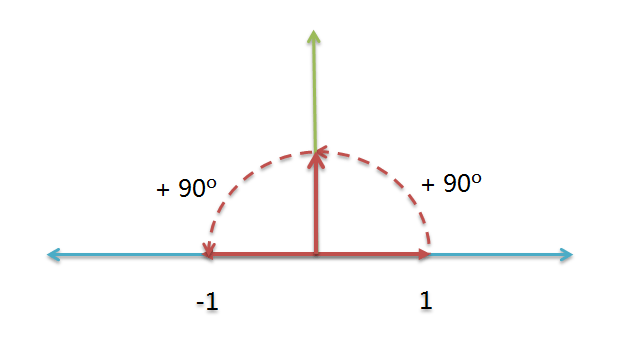
复数：一个复数 x 可以表示为 $x=a+bi$，当 b=0 的时候，这个复数为实数。我们可以把一个复数看作以上平面内的一个点 (a,b)。其中，$a$叫做复数的实部，$b$叫做虚部。
共轭复数: 两个实部相等，虚部为相反数的复数。
模: 即复数的绝对值，用向量来表示复数时的长度，量化一下就是 $\sqrt {a^2+b^2}$

复数的三角形式

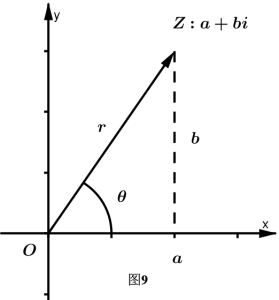
如图所示，其中 $\theta$叫做复数的辐角，幅角可以表示为 $\theta+2k \pi$的形式，而小于 180°的幅角叫做复数的幅角的主值，两个复数相等当且仅当它们的模和幅角的主值相等。
记 r 为复数 x 的模，则 $x=r(\cos \theta +i \sin \theta)$叫做复数的三角形式。

复数的运算

复数的运算也满足实数的运算法则。

加减

代数式:$(a+bi)+(c+di)=(a+c)+(b+d)i$
三角式：满足矢量运算法则

乘除

代数式:$(a+bi)(c+di)=ac+bci+adi-bd=(ac-bd)+(bc+ad)i$
三角式:
$r_1(\cos \theta_1+i \sin \theta_1)r_2(\cos \theta_2+i \sin \theta_2)=$
$r_1 r_2 (\cos (\theta_1 + \theta_2)+\sin(\theta_1+\theta_2))$
也就是积的模等于各复数模的积，积的幅角等于各复数幅角的和。

单位根

n 次单位根即能够满足方程 $\omega^n=1$的复数
由复数的三角式乘除运算法则可以得到，有 n 个这样的复数，它们分布于平面的单位圆上，并平分这个单位圆。
n 次单位根就是：$$e^{\frac{2 \pi ki}{n}},k=0,1,2,…,n-1$$
还有一个很牛的公式，叫做欧拉公式:
$$e^{\theta i}=\cos \theta + i \sin \theta$$
就可以知道 n 次单位根的算数表示法了。记 $\omega_n=e^{\frac{2 \pi i}{n}}$

多项式

参考博客

多项式乘法

给定多项式 $A(x)=\sum_{i=0}^n a_i x^i$和 $B(x)=\sum_{i=0}^n b_i x^i$，则它们的积是：
$$C(x)=\sum_{j+k=i,0 \leq j,k \leq n} a_j b_k x^i$$

点值表示法

我们可以取若干个 x 取值 ${x_0,x_1,…}$，那么多项式 $A(x)$的点值表示法就是 $A={(x_0,A(x_0)),(x_1,A(x_1))…}$
比如说多项式 $A(x)=2x^2+x-1$的点值表达式就可以是 $A={(0,-1),(1,2),(2,9)}$
对于一个次数从 0 到 n-1 的多项式，要取 n 个点才能把它确定下来。
有了点值表示法后，多项式乘法就可以化为 $A={(x_0,A(x_0))…}$和 $B={(x_0,B(x_0))…}$的乘积为 $C={(x_0,A(x_0)B(x_0))…}$了，现在我们只需要迅速地完成点值表示法与代数表示法之间的转化即可。

快速傅里叶变换

参考博客（没错就是数王 dalao 的博客）

折半引理

对于 n 大于 0 且 n 为奇数
$$\{ \omega_n^{2k}|0 \leq k \leq n,k \in Z \}= \{ \omega_{n/2}^k|0 \leq k \leq n/2,k \in Z \}$$
因为集合要去重嘛。
证明:
$ (\omega_{n}^{k+\frac{n}{2}})^2=\omega_n^{2k+n}=\omega_n^{2k} \omega_n^n=(\omega_n^k)^2=\omega_{n/2}^k$
如果上式有哪里不懂的话，我猜你八成是忘了 $\omega_n=e^{\frac{2 \pi i}{n}}$这件事了。

快速傅里叶变换

即将多项式快速转化为点值表示法。
首先，对原多项式做奇偶性划分：
$$A_0(x)=a_0+a_2x+a_4x^2+…+a_{n-2}x^{\frac{x}{2}-1}$$
$$A_1(x)=a_1+a_3x+a_5x^2+…+a_{n-1}x^{\frac{x}{2}-1}$$
所以 $A(x)=A_0(x^2)+xA_1(x^2)$
我们把这个变成点集表达式的时候，可以取一些特殊的 x 来加速，比如，复数 $\omega_n^k$
所以 $A(\omega_n^k)=A_0((\omega_n^k)^2)+\omega_n^kA_1((\omega_n^k)^2)$
由于 $(e^{\frac{2 \pi i}{n}})^{2k}=(e^{\frac{4 \pi i}{n}})^k$
所以 $A(\omega_n^k)=A_0(\omega_{n/2}^k)+\omega_n^k A_1(\omega_{n/2}^k)$
又由折半引理，同时 $\omega_n^{k+\frac{n}{2}}=(e^{\frac{2 \pi i}{n}})^{k+\frac{n}{2}}=(e^{\frac{2 \pi i}{n}})^k e^{\pi i}=\omega_n^k \omega_n^{\frac{n}{2}}=-\omega_n^k$
所以得到 $A(\omega_n^{k+n/2})=A_0(\omega_{n/2}^k)-\omega_n^k A_1(\omega_{n/2}^k)$
当 k 取遍 $[0,\frac{n}{2}-1]$时，$k+\frac{n}{2}$就会取遍 $[\frac{n}{2},n-1]$
这样我们可以利用分治，迅速将多项式转化成点值表示法了，复杂度为 $O(n log_2n)$

逆离散快速傅里叶变换

即将点值表示法快速转化为多项式
这相当于是一个解方程的过程，方程可以写作矩阵 (1)，下图摘自树王 dalao 的博客。

所以呢 $e_{ij}=\sum_{k=0}^{n-1}d_{ik}v_{kj}=\sum_{k=1}^n\omega_n^{-ik}\omega_n^{kj}=\sum_{k=1}^n\omega_n^{k(j-i)}$
然后当 i=j 时，显然 $e_{ij}=n$
当 i 不等于 j 时，显然 $e_{ij}=\sum_{k=0}^{n-1} \omega_n^{(j-i)k}$，然后根据等比数列随便搞一搞得到：
$$e_{ij}=\frac{(\omega_n^n)^{j-i}-1}{\omega_n^{j-i}-1}=0$$
所以 $\frac{1}{n} E_n=I_n$($I_n$表示 n×n 的单位矩阵)，也就是 $\frac{1}{n}D=V^{-1}$
那么：

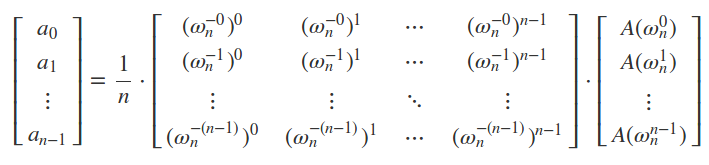
而这个 D 矩阵真是完美，可以和类似于快速傅里叶变换的方法搞定，就大大减小了代码复杂度

蝶形算法

参考博客
例题：洛谷 P3803
又名蝴蝶操作，Cooley-Tukey 算法。
这个名字非常优美，这个算法也很优美，就是…… 有点令人痛苦…… 不过，这仅仅是理解上的痛苦而已，比你被卡常成 TLE 的痛苦还是要好一点。
我们手动模拟一个递归过程，每次把偶数位放在前面，奇数位放在后面处理。第一行和第二行表示当前位置的数的二进制形式。那么（下表依旧摘抄自数王 dalao）：
$$
\begin{align}
\begin{matrix}
&000\ &001\ &010\ &011\ &100\ &101\ &110\ &111\\
&0\ &1\ &2\ &3\ &4\ &5\ &6\ &7\\
&0\ &2\ &4\ &6\ &1\ &3\ &5\ &7\\
&0\ &4\ &2\ &6\ &1\ &5\ &3\ &7\\
&0\ &4\ &2\ &6\ &1\ &5\ &3\ &7\\
&000\ &100\ &010\ &110\ &001\ &101\ &011\ &111
\end{matrix}
\end{align}
$$
发现位置最后的数，是其二进制反过来后得到的数。其实证明也很容易，我们因为按照奇偶划分，会把末尾是 1 的放后面，末尾是 0 的放前面。然后把倒数第二位是 0 的放前面，是 1 的放后面…… 算法步骤：
1. 将二进制反序后的序列处理出来。
2. 枚举当前处理的区间长度 $2i$（至于为什么要乘 2，因为代码里乘了 2，此处 i 不是虚数单位）
3. 根据欧拉公式计算 $\omega_{2i}$
4. 枚举每个区间开头 j
5. 枚举该区间的每个偶数位那一半的 $a_{j+k}$和奇数位那一半的 $a_{i+j+k}$
6. 令 $t1=a_{j+k}$，$t2=\omega_{2i}^k a_{i+j+k}$，那么更改 $a_{j+k}=t1+t2$，$a_{i+j+k}=t1-t2$。由于这个操作的流程像蝴蝶的翅膀，所以该算法称为蝶形算法。
代码如下：

#include<bits/stdc++.h>
using namespace std;
#define db double
const int N=2650000;//注意空间
const db pi=3.1415926535897384626;
struct com{db r,i;}a[N],b[N];//复数
int n,m,len,rev[N];
com operator + (com A,com B) {return (com){A.r+B.r,A.i+B.i};}
com operator - (com A,com B) {return (com){A.r-B.r,A.i-B.i};}
com operator * (com A,com B) {return (com){A.r*B.r-A.i*B.i,A.i*B.r+A.r*B.i};}
com operator / (com A,db  B) {return (com){A.r/B,A.i/B};}
void FFT(com *a,int x) {
    for(int i=0;i<n;++i) if(i<rev[i]) swap(a[i],a[rev[i]]);//防止两次交换
    for(int i=1;i<n;i<<=1) {//步骤 2
        com wn=(com){cos(pi/i),x*sin(pi/i)};//步骤 3
        for(int j=0;j<n;j+=(i<<1)) {//枚举区间开头，步骤 4
            com w=(com){1,0},t1,t2;
            for(int k=0;k<i;++k,w=w*wn)//步骤 5
                t1=a[j+k],t2=w*a[j+k+i],a[j+k]=t1+t2,a[j+k+i]=t1-t2;
        }
    }
    if(x==-1)for(int i=0;i<n;i++)a[i]=a[i]/n;
}
int main() {
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;++i) scanf("%lf",&a[i].r);
    for(int i=0;i<=m;++i) scanf("%lf",&b[i].r);
    m=n+m; for(n=1;n<=m;n<<=1) ++len;
    for(int i=0;i<n;++i) rev[i]=(rev[i>>1]>>1)|((i&1)<<(len-1));//二进制下的翻转，步骤 1
    FFT(a,1),FFT(b,1);
    for(int i=0;i<=n;++i) a[i]=a[i]*b[i];
    FFT(a,-1);
    for(int i=0;i<=m;++i) printf("%d ",(int) (a[i].r+0.5));
    return 0;
}

原根

小 L 学会 FFT 后，自以为非常牛逼，于是要 dalao 给她道题水水。dalao 随手给了她一道……
卡精度的题。

在快速傅里叶变换里，我们利用 $\omega_n$实现了对于消去引理和折半引理的满足。那么，有没有什么整数也满足呢？
原根就满足。
what is 原根 you may ask
定义 P 的原根为满足 $g^{\phi(P)} \equiv 1 (\bmod P )$的整数 g，请记住这个定义。
对于一个质数 P, 如果它存在原根，那么 $g^i ≠ g^j$。由于这条性质，所以我们可以利用原根来生成点集表示法。

快速数论变换

参考博客
现在我们用 $g^{\frac{\phi(P)}{n}}$来代替 $\omega_n$进行计算。
对于 P 的要求：要求 $\frac{\phi(P)}{n}$为整数，又因为当 P 为质数时，$\phi(P)=P-1$，所以 $P=k2^q+1$，其中 $2^q \geq n$
原根是否可以代替单位根，取决于 FFT 的引理，原根是否也满足，以折半引理为例, 在模 P 的意义下：
$$(g^{\frac{\phi(P)}{n}})^2=g^{\frac{2\phi(P)}{n}}=g^{\frac{\phi(P)}{n/2}}$$
$$(g^{\frac{\phi(P)}{n}})^{k+\frac{n}{2}}=g^{\frac{\phi(P)}{2}}(g^{\frac{\phi(P)}{n}})^k=-(g^{\frac{\phi(P)}{n}})^k$$
所以是满足的，其他的东西推导也类似啦。
那么怎么求原根呢？用 bsgs 打表。除非题目给你模数，否则可以一劳永逸地选择几个记住：一位 dalao 的归纳（好像 g=3,k=23,r=119 很受欢迎的样子？）
如果 P 不是个质数，就用中国剩余定理玩合并。
但是以上两个过程都比较痛苦就是了…… 给出 NTT 模板的代码，例题还是上面那道：

#include<bits/stdc++.h>
using namespace std;
const int G=3,mod=(119<<23)+1,N=2650000;
int n,m,len,a[N],b[N],rev[N];
int ksm(int x,int y) {
    int re=1;
    while(y) {
        if(y&1) re=1LL*re*x%mod;
        x=1LL*x*x%mod,y>>=1;
    }
    return re;
}
void NTT(int *a,int x) {
    for(int i=0;i<n;++i) if(i<rev[i]) swap(a[i],a[rev[i]]);
    for(int i=1;i<n;i<<=1) {
        int gn=ksm(G,(mod-1)/(i<<1));
        for(int j=0;j<n;j+=(i<<1)) {
            int t1,t2,g=1;
            for(int k=0;k<i;++k,g=1LL*g*gn%mod) {
                t1=a[j+k],t2=1LL*g*a[j+k+i]%mod;
                a[j+k]=(t1+t2)%mod,a[j+k+i]=(t1-t2+mod)%mod;
            }
        }
    }
    if(x==1) return;
    int ny=ksm(n,mod-2); reverse(a+1,a+n);//在 FFT 里面，我们已经利用 x 在步骤 3 中完成了翻转。
    for(int i=0;i<n;++i) a[i]=1LL*a[i]*ny%mod;
}
int main() {
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;++i) scanf("%d",&a[i]);
    for(int i=0;i<=m;++i) scanf("%d",&b[i]);
    m=n+m;for(n=1;n<=m;n<<=1)++len;
    for(int i=0;i<n;++i) rev[i]=(rev[i>>1]>>1)|((i&1)<<(len-1));
    NTT(a,1),NTT(b,1);
    for(int i=0;i<n;++i) a[i]=1LL*a[i]*b[i]%mod;
    NTT(a,-1);for(int i=0;i<=m;++i) printf("%d ",a[i]);
    return 0;
}

应用

bzoj4503

将某一元素翻转来构成卷积，是一种常用手段。那么我们将 B 串翻转，字母全部转化为数字，”?” 转化为 0 之后，我们得到 A 从位置 j 开始能和 B 匹配的要求是：
$$C_{j+m-1}=\sum_{i=0}^{m-1}(a_{j+i}-b_{m-i-1})^2*b_{m-1-i}=0$$
展开发现是三个卷积的和，分别用 FFT 或者 NTT 搞一搞，查找为 0 的 C 值即可。

bzoj4827/洛谷 P3723

假设增加的值为 C, 差异值公式：
$$\sum_{i=0}^{n-1}(a_i+C-b_i)^2=\sum_{i=0}^{n-1}a_i+\sum_{i=0}^{n-1}b_i+nC^2-2\sum_{i=0}^{n-1}a_ib_i+2C\sum_{i=0}^{n-1}(a_i-b_i)$$
假定 C 为一个常数，那么这个式子有一堆的常数，主要矛盾是求最大的 $2\sum_{i=0}^{n-1}a_ib_i$，那么将 B 手链翻转后用 FFT 或 NTT 搞一搞即可。
最后，可以枚举 C 或者利用二次函数搞定和 C 有关的最优值。

bzoj3527/洛谷 3338

可得 $$E_i=\sum_{j=1}^{i-1} \frac{q_j}{(i-j)^2}-\sum_{j=i+1}^n\frac{q_j}{(i-j)^2}$$
令 $a_i=q_i$，$b_i=\frac{1}{i^2}$，可以发现 $\frac{q_j}{(i-j)^2}=a_jb_{i-j}$
原式就是两个卷积相减，后一个卷积需要反向来构造。