题意:
给定一个”A-structure” 的定义:
If V=(A,B,C,D) and E=(AB,BC,CD,DA,AC), we call G as an “A-structure”.
求图 G 中有多少个”A-structure”?
数据范围:对于每组数据点数和边数都小于 $2 \times 10^5$,对于所有数据,总点数小于 $3 \times 10^5$,总边数小于 $6 \times 10^5$
吐槽:
其实这道题对 dalao 们来说应该是一道简单套路题,可是对我这种蒟蒻来说这个构造方法的思路还是挺新颖的。
思路:
“A-structure” 的实质就是两个三元环组成的,所以我们只要统计每条边参与了多少个三元环的组成,然后再用这个数套一下组合数就行啦。
对于统计三元环:考虑把整个图中的无向边变成有向边,且有向边是从原来的无向图中度数小的点连向度数大的点,度数相同的从小编号连向大编号,很容易知道新得到的这个图是一个有向无环图。且原图中的三元环结构都无一例外地变成了这种样子:
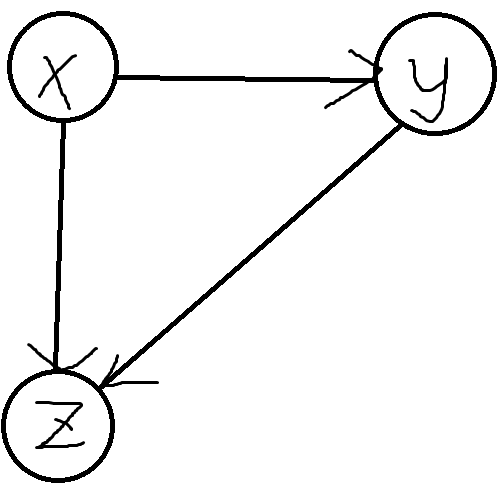
三元环无向边转有向边
为什么要这样构造呢?我们会发现这样构造会有一个重要结论:不可能有一个点的出度大于 $\sqrt{2m}$
证明:记一个点 $i$出度为 $out[i]$, 假设 $out[i]=k>\sqrt{2m}$,记这 $k$条边连出去的点分别为 $d_1,d_2,\cdots,d_k$,根据连边时的规则:有向边从原来的无向图中度数小的点连向度数大的点,我们可以知道,这些点的度数是肯定是大于 $\sqrt{2m}$的,所以这些点的总度数大于 $\sqrt{2m}$,而它们的总度数上界就是 $2m$(每条边会被算两次,整个图总度数为 $2m$),因此假设不成立。Q.E.D(tip: 听说实际上点出度的量级是 $\sqrt{n}$的,不过我不太会证明,若有 dalao 会证明的话请在评论区发挥 QAQ)
因此我们可以枚举每一条边,对于它的起点 $u$,枚举 $u$能到达的所有点并标记一下,对于它的终点 $v$,枚举 $v$所能到达的点,若它已经被标记过了,我们就令 $ans++;$,由上面的证明,出度的量级是 $\sqrt{m}$的,因此这个算法的时间复杂度是 $\Theta(m\sqrt{m})$
代码:
#include<bits/stdc++.h>
#define R register
#define fo(i, a, b) for (R int i = (a); i <= (b); ++i)
#define ll long long
#define N 600005
int n, m, cnt[N], head[N], nxt[N], to[N], tans, p[N], q[N];
ll ans;
std::vector <int> e[N];
struct edge{
int u, v;
}in[N];
int fl[N], tmp;
inline void add (int x, int y, int cnt)
{
nxt[cnt] = head[x];
head[x] = cnt;
to[cnt] = y;
}
int main()
{
while (scanf("%d %d", &n, &m) && n != 0 && m != 0)
{
memset(head, -1, sizeof(head));
memset(p, 0, sizeof(p));
ans = 0;
fo (i, 1, m)
{
scanf("%d %d", &in[i].u, &in[i].v);
cnt[in[i].u]++;
cnt[in[i].v]++;
}
fo (i, 1, m)
{
if (cnt[in[i].u] > cnt[in[i].v])
std::swap(in[i].u, in[i].v);
add(in[i].u, in[i].v, i);
}
fo (i, 1, m)
{
tans = 0;
int u = in[i].u;
int v = in[i].v;
tmp++;
for (int j = head[u]; j != -1; j = nxt[j])
{
fl[to[j]] = tmp;
q[to[j]] = j;
}
for (int j = head[v]; j != -1; j = nxt[j])
if (fl[to[j]] == tmp)
{
p[j]++;
p[i]++;
p[q[to[j]]]++;
}
}
fo (i, 1, m)
ans = 1LL * ans + 1LL * p[i] * (p[i] - 1) / 2;
printf("%lld\n", ans);
}
return 0;
}
0 条评论