【题解】Counting Stars 三元环计数 hdu – 6184 ——quhengyi11

题意：

给定一个”A-structure” 的定义：

If V=(A,B,C,D) and E=(AB,BC,CD,DA,AC), we call G as an “A-structure”.

求图 G 中有多少个”A-structure”？

数据范围：对于每组数据点数和边数都小于 $2 \times 10^5$，对于所有数据，总点数小于 $3 \times 10^5$，总边数小于 $6 \times 10^5$

吐槽：

其实这道题对 dalao 们来说应该是一道简单套路题，可是对我这种蒟蒻来说这个构造方法的思路还是挺新颖的。

思路：

“A-structure” 的实质就是两个三元环组成的，所以我们只要统计每条边参与了多少个三元环的组成，然后再用这个数套一下组合数就行啦。

对于统计三元环：考虑把整个图中的无向边变成有向边，且有向边是从原来的无向图中度数小的点连向度数大的点，度数相同的从小编号连向大编号，很容易知道新得到的这个图是一个有向无环图。且原图中的三元环结构都无一例外地变成了这种样子：

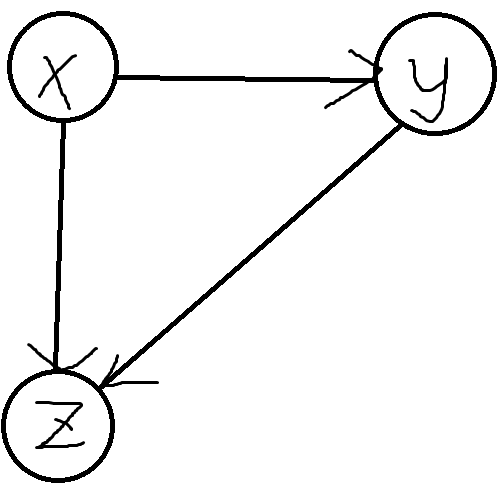
三元环无向边转有向边

为什么要这样构造呢？我们会发现这样构造会有一个重要结论：不可能有一个点的出度大于 $\sqrt{2m}$

证明：记一个点 $i$出度为 $out[i]$， 假设 $out[i]=k>\sqrt{2m}$，记这 $k$条边连出去的点分别为 $d_1,d_2,\cdots,d_k$，根据连边时的规则：有向边从原来的无向图中度数小的点连向度数大的点，我们可以知道，这些点的度数是肯定是大于 $\sqrt{2m}$的，所以这些点的总度数大于 $\sqrt{2m}$，而它们的总度数上界就是 $2m$（每条边会被算两次，整个图总度数为 $2m$），因此假设不成立。Q.E.D（tip: 听说实际上点出度的量级是 $\sqrt{n}$的，不过我不太会证明，若有 dalao 会证明的话请在评论区发挥 QAQ）

因此我们可以枚举每一条边，对于它的起点 $u$，枚举 $u$能到达的所有点并标记一下，对于它的终点 $v$，枚举 $v$所能到达的点，若它已经被标记过了，我们就令 $ans++;$，由上面的证明，出度的量级是 $\sqrt{m}$的，因此这个算法的时间复杂度是 $\Theta(m\sqrt{m})$

代码：

#include<bits/stdc++.h>
#define R register
#define fo(i, a, b) for (R int i = (a); i <= (b); ++i)
#define ll long long
#define N 600005
int n, m, cnt[N], head[N], nxt[N], to[N], tans, p[N], q[N];
ll ans;
std::vector <int> e[N];
struct edge{
    int u, v;
}in[N];
int fl[N], tmp;
inline void add (int x, int y, int cnt)
{
    nxt[cnt] = head[x];
    head[x] = cnt;
    to[cnt] = y;
}
int main()
{
    while (scanf("%d %d", &n, &m) && n != 0 && m != 0)
    {
        memset(head, -1, sizeof(head));
        memset(p, 0, sizeof(p));
        ans = 0;
        fo (i, 1, m)
        {
            scanf("%d %d", &in[i].u, &in[i].v);
            cnt[in[i].u]++;
            cnt[in[i].v]++;
        }
        fo (i, 1, m)   
        { 
            if (cnt[in[i].u] > cnt[in[i].v])
                std::swap(in[i].u, in[i].v);
            add(in[i].u, in[i].v, i);
        }
        fo (i, 1, m)
        {
            tans = 0;
            int u = in[i].u;
            int v = in[i].v;
            tmp++;
            for (int j = head[u]; j != -1; j = nxt[j])
            {
                fl[to[j]] = tmp;
                q[to[j]] = j;
            }
            for (int j = head[v]; j != -1; j = nxt[j])
                if (fl[to[j]] == tmp)
                {
                    p[j]++;
                    p[i]++;
                    p[q[to[j]]]++;
                }
        }
        fo (i, 1, m)
            ans = 1LL * ans + 1LL * p[i] * (p[i] - 1) / 2;
        printf("%lld\n", ans);
    }
    return 0;
}