带权二分

例题

给定一个非负整数序列，将它划分为 k 段，最小化每段的平方和。

朴素做法

设 $f[i][j]$为前 $i$项划分为 $j$段的最小平方和。
$$
f[i][j]=min(f[u][j-1]+(S[i]-S[u])^2)
$$
该做法的时间复杂度为 $O(n^2k)$。

更快的做法

运用斜率优化，可以将时间复杂度优化至与状态数同阶:$O(nk)$。

能不能再快一点

这就要用到本文所介绍的一类 Dp 优化方法：带权二分。又称 wqs 二分。

算法思想

这个算法思想源于对 Dp 的一种感性的理解。

假设我们并不关心这个序列究竟分了几段，我们只想让最小值尽量小，那么 Dp 算法最终肯定会把这个序列分成 n 段。

假设我们不希望算法分太多段，我们可以在每新建一段的同时给这一段增加一个附加权值 C，这样，算法会在” 分得多原权值小” 和” 分的少附加权值小” 两者之间找到平衡点，找到最小的值。

感性地理解，这个附加权值 C 越大，分的段数应该越少；附加权值 C 越小，分的段数应该越多。因此，我们可以通过改变附加权值 C 从而同时控制段数和最小值。

通过这一点，我们可以使分的段数恰好小于等于 k。我们猜测：这时的解减去附加权值就是段数等于 k 时的最优解。

理性证明

刚才的思想大意中，我们忽略了两个严重的问题：

• 我们有可能没法通过改变附加权值使得分的段数等于 k，因为有可能段数关于附加权值的函数不连续。
• 我们还没有证明通过改变附加权值求得的解一定是最优解。

下面将利用理性解决这两个问题。

将问题函数化

我们建立 “最小平方和” 关于 “段数” 的函数。

通过一些简单的证明或者打表可以发现，这个函数其实是下凸的。函数的凸性是带权二分得以存在的基础。原因待会具体分析。

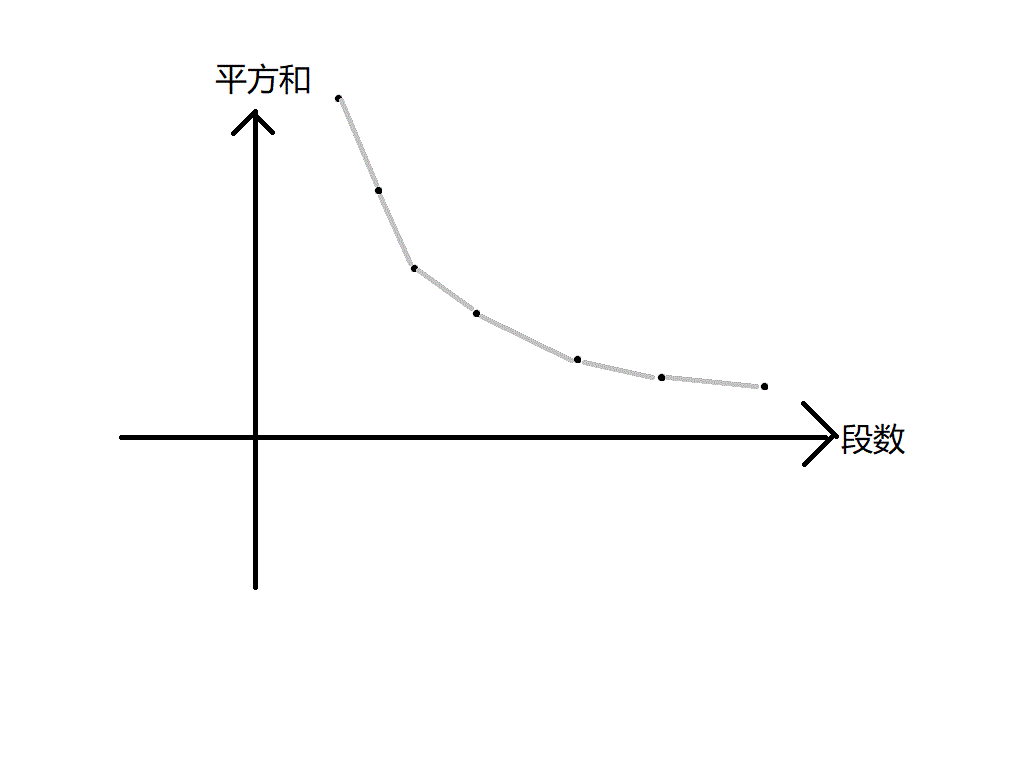
当我们给 dp 增加附加权值，也就意味着给函数图像加上 $y=cx$。一个下凸函数加上一个一次函数后一定还是个下凸函数，所以新的函数图像依旧下凸。

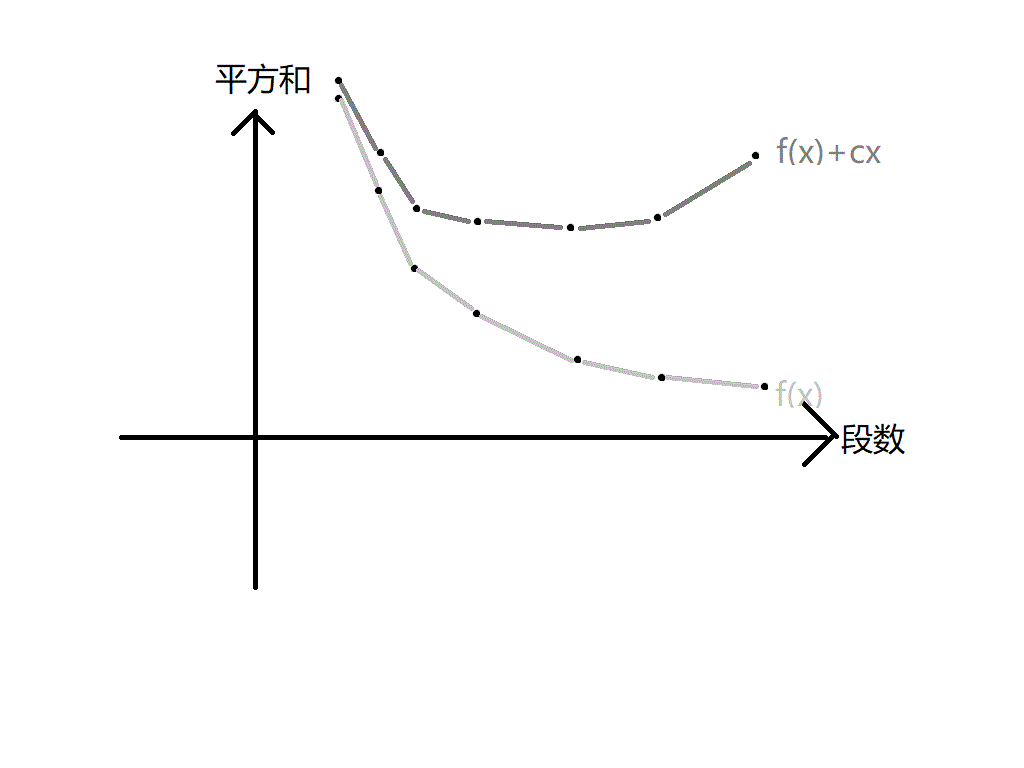
这时，我们用斜率优化 dp 求出的最小值就是函数纵坐标最小的点。而这个点实际上也是 $y=-cx$与函数图像的切点。

现在我们就可以说明第一个问题：我们是否可能无法找到恰好 k 段的情况。

如果函数图像存在共线的三点，那么中间的那个点往往取不到。因为无论如何一条直线都不会与那个点相切。因此那个点横坐标代表的段数是永远取不到的。不过，如果我们找到了与他共线的那些点的最左边的点，我们就可以通过左边那个点直接推出他的答案，因此这个问题解决了。

第二个问题可以直接通过函数的凸性证明：为什么通过改变附加权值取到的解一定最优。

由于函数是下凸的，而我们的方法是 “找切线”，所以我们最终切到的点一定可以覆盖函数上所有的点 (共线的情况除外)，又由于共线时线段中间的点可以通过线段端点推算出来，所以每个点的纵坐标都是可以通过 “找切线” 的方法唯一最优确定的，因此我们找到的解一定也是最优解。

接下来说说为什么非凸函数不可行：如果函数非凸，那么存在点不在凸包上，那么我们永远也无法通过 “找切线” 的方式找到那个点，因此这个点的最优值无法确定。

总结一下

如果我们在 dp 时需要找一个变量 $y$的最小值，但是需要保证另一个变量 $x=x_0$，同时，$y=f(x)$的函数图像满足一定的凸性 (最小化 $y$下凸，最大化 $y$上凸)，这时，我们就可以二分一条代表着附加权值的切线，一步步逼近 $x=x_0$的点。

在 dp 时，我们需要保证: 在 dp 的所有最优解中，返回的一定是 $x$最小的，这样，如果存在共线的三点，我们找到的是最靠左的一个。

当附加权值为 $c$时，最终找到的点 $(x,y)$有两种可能：

• 1: $x=x_0$，那么答案就是：$y-x_0\cdot c$
• 2: $x<x_0$，那么答案也是：$y-x_0\cdot c$

其中第二种情况就是之前说的 “由最左侧共线点推出中间点”。画个图自己就明白了。

一些疑问

Q. 如果要输出方案呢？

A. 不好办

当我们最终找到的点满足 $x=x_0$时，方案就是正确的方案。

但是如果 $x<x_0$，这时我们的方案就不对。

那么能不能在函数图像上做做手脚，使每个点都暴露出来，使他们每个都能被一条直线所切？

理论上是可以的，但是如果采用加上 $y=x^2$之类的凸函数，经过我的测试，会导致 dp 具有后效性而出错。

Update:

时隔一年，我终于找到了一种可以输出方案的方法。

我们枚举被分割出的第一段，并判断这样分割之后是否仍然合法（即平方和最小，且剩下的部分存在一种合法分割方式使得总共被分成 $k-1$段）。这样，我们就将问题递归解决即可。

Q. 这种算法能否拓展到二维情况呢？

A. 好办

如果我们 dp 时需要同时满足 $x=x_0,y=y_0$，并且最小化 $z$，这就相当于找一个三维凸函数的切面。然而这好像很困难。

按照之前的套路，我们可能需要二分 $c_x$的同时套上二分 $c_y$。有人可能会想，能不能用两次二分，第一次确定 $c_x$，第二次确定 $c_y$，两次的结果组合中在一起就是答案？这样是不对的，因为固定 $c_x$，改变 $c_y$，切点的 $x$坐标可能发生变化。实际上，所有 $y$坐标是 $y_0$的点也构成一个凸函数，所以用二分套二分才是可以的。

可是，哪里来的出题人会畸形到找到一种二维的带权二分的模型并且出成题目呢？