题目
依旧是那个可爱的传送门酱 (^o^)
求树上每个点到其它点的距离的 k 次方和,In formal:ans[u]=∑v∈Vdis(u,v)k
k<=150 n<=5e4
题解
这道题就是一个推柿子了啦。
qhy 作为一个喜欢吃柿子的女孩子,不知道很多众所周知的公式,下面这个就是其中一个 (S 表示第二类 Stirling 数):
xn=x∑k=0SknAkx
如何证明呢?我们先口胡一下组合意义,左边相等于将 n 个有序号的柿子随便放进 x 个有序号的碗里(可以有空碗),右边相当于枚举放柿子的碗的个数 k,先从 x 个碗里有顺序地选 k 个碗,再将 n 个有序号的柿子放进这 k 个碗。
推公式版本的证明我就直接贴一个《具体数学》上的了(不过组合这东西还是记组合意义比较乐滋滋):
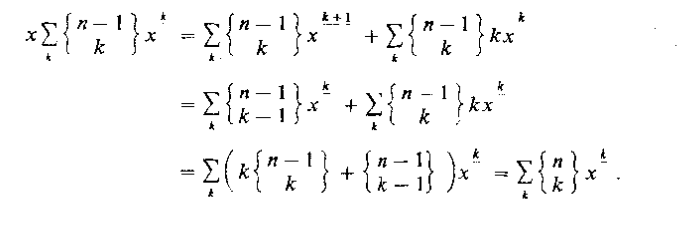
好了那么我们现在把要求的柿子套上去化一下
ans[u]=∑v∈Vk∑j=0SjkAjdis(u,v)
因为有 pascal 恒等式:
C(n,m)=C(n−1,m−1)+C(n,m−1)我们考虑将 A 拆掉
ans[u]=∑v∈Vk∑j=0SjkCjdis(u,v)×j!
交换枚举顺序
ans[u]=k∑j=0Sjkj!∑v∈VCjdis(u,v)
第二个 sum 前面显然是可以 k²预处理并且 k 时间计算的,我们考虑如何将后面的部分算出来。
记 f[u][i]表示 ∑v∈VCidis(u,v),说人话就是 u 点到其它各点的距离和各种鬼东西
其实这个就是一个树形 dp 的事情,nk 的复杂度就能跑出来,注意一下细节就行。
还是多说一下吧。
首先从上往下做一次 dp,计算出 ∑v∈subtree(v)Cidis(u,v),然后从下往上做一次 dp,稍微用一下 pascal 恒等式就行了。(不清楚就看代码吧)
代码:
#include<bits/stdc++.h>
#define fo(i, a, b) for (int i = (a); i <= (b); ++i)
#define fd(i, a, b) for (int i = (a); i >= (b); --i)
#define edge(i, u) for (int i = head[u], v = e[i].v; i; i = e[i].nxt, v = e[i].v)
#define N 50505
#define KK 155
#define pb push_back
#define F first
#define S second
#define ll long long
#define inf 1000000007
#define mp std::make_pair
#define lowbit(x) (x & -x)
#define ls (k << 1)
#define rs (k << 1 | 1)
#define mod 10007
#define eps 1e-4
int n, K, u, v, head[N], s[KK][KK], fac[KK];
int f[N][KK], g[KK];
struct edge{
int nxt, v;
}e[N << 1];
int tot;
inline void addedge (int u, int v)
{
e[++tot] = (edge) {head[u], v};
head[u] = tot;
}
inline void dfs1 (int u, int fa)
{
f[u][0] = 1;
edge (I, u)
{
if (v == fa) continue;
dfs1(v, u);
f[u][0] = f[u][0] + f[v][0];
fo (i, 1, K)
f[u][i] = (f[u][i] + f[v][i] + f[v][i - 1]) % mod;
}
}
inline void dfs2 (int u, int fa)
{
edge (I, u)
{
if (v == fa) continue;
g[0] = f[u][0] - f[v][0];
fo (i, 1, K)
g[i] = (f[u][i] - f[v][i - 1] - f[v][i]) % mod;
f[v][0] = f[v][0] + g[0];
fo (i, 1, K)
f[v][i] = (f[v][i] + g[i - 1] + g[i]) % mod;
dfs2(v, u);
}
}
int main ()
{
scanf("%d %d", &n, &K);
s[0][0] = 1;
fo (i, 1, K)
fo (j, 1, i)
s[i][j] = (s[i - 1][j - 1] + j * s[i - 1][j]) % mod;
fac[1] = 1;
fo (i, 2, K) fac[i] = fac[i - 1] * i % mod;
fo (i, 2, n)
{
scanf("%d %d", &u, &v);
addedge(u, v);
addedge(v, u);
}
dfs1(1, 0);
dfs2(1, 0);
fo (u, 1, n)
{
ll ans = 0;
fo (i, 0, K)
ans = (ans + s[K][i] * fac[i] % mod * f[u][i] % mod) % mod;
printf("%lld\n", (ans % mod + mod) % mod);
}
return 0;
}
5 条评论
quhengyi11 · 2018年11月8日 4:46 下午
害怕.jpg(我怎么感觉 dalao 误解了什么 QAQ
boshi · 2018年11月8日 2:11 下午
你们这是性别歧视
B_Z_B_Y · 2018年11月8日 2:32 下午
哎, ~~~~~(长叹 = =
XZYQvQ · 2018年11月5日 11:02 下午
捕捉亮点 QwQ:
quhengyi11 · 2018年11月6日 10:35 上午
嘤嘤嘤 qwq(请自行脑补女孩子的声音