考场上看到 D2T3 的时候就蒙了,觉得是什么毒瘤计数法,后来听别人说是猫锟在去年冬令营的时候讲的毒瘤算法动态 dp 板子题?然后感觉自己好亏(去年我都去不了冬令营 QAQ)于是决定学一学。
顾名思义,动态 dp,就是给你一个可以静态 dp 的题,然后带一些修改操作和询问操作来瞎搞的。一般修改的东西一定是比较局部的,因此我们可以在修改后用低于 n 的复杂度维护这个东西。
说了这么多奇怪的概念我估计你也看不懂,那就根据例题讲吧。
题意很简单,就是在错位的要求下求最大乘积和,显然如果没有这个错位的要求,两个数组排序根据排序不等式顺序和最大可以知道对应位相乘就行了。那加上错位的要求怎么做呢?我们可以脑补出一幅图,每个人都是在满足要求的前提下选在排序后数组中离自己能力值排位比较近的马。然而这个比较近的马究竟是多近呢?我们可以推如下结论:
设排序后的能力值第 i 位的人匹配能力值排序后第 j 位的马,我们有 $|i-j|\leq 2$
怎么推呢,我们可以用一下简单的反证就可以证明了。
由对称性,我们只考虑 $j\lt i$的状况
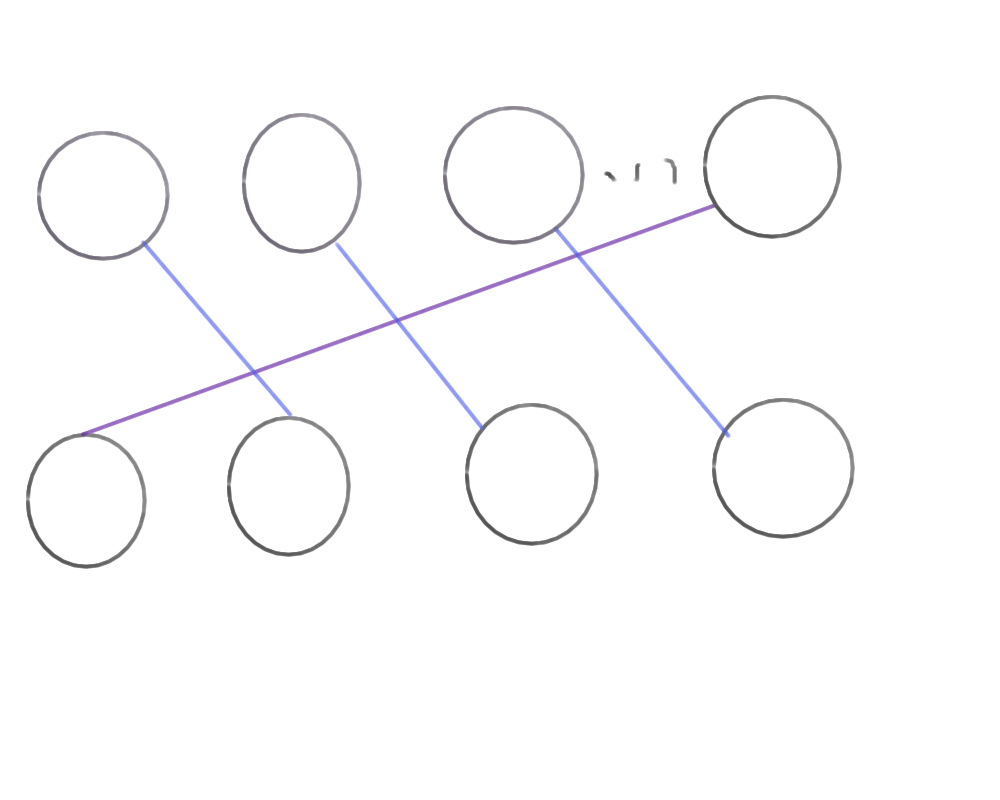
对于紫色线的这样一种匹配情况,我们总能在 $i$号人之前找到这样与紫色线交叉的匹配,假设当前与 $i$匹配的马是 $j$,不妨设这三个人为 $a_1,a_2,a_3$。我们可以发现,在最大的匹配和方案中,任意一对匹配,如果形成了交叉的状况,它们是必定不能交换马的(否则就是由排序不等式,会形成更好的匹配)
我们设 $a_i$的马为 $b_i$,那么 $b_1$可能和 $i$是一对不能匹配的关系或者说 $a_1$和 $j$不能匹配,我们假设是前者吧,那么 $a_2$就只可能是与 $j$不能匹配,那么 $a_3$肯定可以和 $j$匹配并且 $i$肯定和 $b_3$能够匹配,我们调整 $a_3$匹配 $j$,$i$匹配 $b_3$,便是一种更好的匹配。
因此我们知道,每个人的匹配方案只可能有 5 个。
我们这里设 $f[i]$表示前 $i$个人和马匹配完后的最大值,我们容易写出下面的方程(搞了半天 markdown 公式里换不了行我弃疗了我们直接贴代码吧):
if (a[i].id != b[i].id)
f[i] = max(f[i], f[i - 1] + a[i].v * b[i].v);
if (a[i - 1].id != b[i].id && a[i].id != b[i - 1].id)
f[i] = max(f[i], f[i - 2] + a[i - 1].v * b[i].v + a[i].v * b[i - 1].v);
if (a[i - 1].id != b[i].id && a[i - 2].id != b[i - 1].id && a[i].id != b[i - 2].id)
f[i] = max(f[i], f[i - 3] + a[i - 1].v * b[i].v + a[i - 2].v * b[i - 1].v + a[i].v * b[i - 2].v);
if (a[i - 2].id != b[i].id && a[i - 1].id != b[i - 2].id && a[i].id != b[i - 1].id)
f[i] = max(f[i], f[i - 3] + a[i - 2].v * b[i].v + a[i - 1].v * b[i - 2].v + a[i].v * b[i - 1].v);
然后静态我们就说完了。
那么现在我们加上了修改操作,我们怎么动态维护这个东东呢?
我们可以发现,每次我们修改两对的匹配关系,其影响到的方程是很少的,但是由于它的后效性,对最终答案的影响可能是很大的。
那我们咋办啊?
动态 dp 提供了一种思路,因为你只改变了常数级别的转移个数,我们可以将转移写到矩阵里面去,那样就可以用线段树快速维护转移了。
我们将矩阵乘法新定义一下,将原来的 $+$改成取 max,原来的 $\times$改成 $+$,我们可以将转移写成下面的形式 (听说 markdown 又咕咕我用图片吧,更好的体验可以戳这里将 markdown 文本复制到你本地的 markdown 里面)

其中三种 case 就是三个转移,具体可以看代码。
然后线段树快速维护即可。有一个细节就是答案即是所有矩阵乘积的第三行第三列,可以将初始矩阵看成零矩阵理解。
代码
#include<bits/stdc++.h>
#define Re register
#define fo(i, a, b) for (Re int i = (a); i <= (b); ++i)
#define fd(i, a, b) for (Re int i = (a); i >= (b); --i)
#define edge(i, u) for (Re int i = head[u], v = e[i].v; i; i = e[i].nxt, v = e[i].v)
#define pb push_back
#define F first
#define S second
#define ll long long
#define inf 1000000007
#define mp std::make_pair
#define lowbit(x) (x & -x)
#define mod 19260817
#define eps 1e-4
#define itset std::set<node>::iterator
#define lb lower_bound
#define N 300005
#define ls (k << 1)
#define rs (k << 1 | 1)
int n, m, x, y, posa[N], posb[N];
struct node{
ll v;
int id;
friend bool operator < (node x, node y) {return x.v < y.v;}
}a[N], b[N];
struct matrix{
ll t[3][3];
inline void clear () {memset(t, -1, sizeof t);}
inline void getmatrix (int x)
{
clear();
t[1][0] = 0; t[2][1] = 0;
if (a[x].id != b[x].id) t[2][2] = a[x].v * b[x].v;
if (x < 2) return;
if (a[x].id != b[x - 1].id && a[x - 1].id != b[x].id) t[1][2] = a[x].v * b[x - 1].v + a[x - 1].v * b[x].v;
if (x < 3) return;
ll v1 = -1, v2 = -1;
if (a[x].id != b[x - 1].id && a[x - 1].id != b[x - 2].id && a[x - 2].id != b[x].id)
v1 = a[x].v * b[x - 1].v + a[x - 1].v * b[x - 2].v + a[x - 2].v * b[x].v;
if (a[x].id != b[x - 2].id && a[x - 1].id != b[x].id && a[x - 2].id != b[x - 1].id)
v2 = a[x].v * b[x - 2].v + a[x - 1].v * b[x].v + a[x - 2].v * b[x - 1].v;
t[0][2] = std::max(v1, v2);
}
friend matrix operator * (matrix x, matrix y)
{
matrix c; c.clear();
fo (i, 0, 2)
fo (k, 0, 2) if (x.t[i][k] != -1)
fo (j, 0, 2) if (y.t[k][j] != -1)
c.t[i][j] = std::max(c.t[i][j], x.t[i][k] + y.t[k][j]);
return c;
}
}c[N << 2], tmp;
inline void build (int k, int l, int r)
{
if (l == r) {c[k].getmatrix(l); return;}
int mid = l + r >> 1;
build(ls, l, mid); build(rs, mid + 1, r);
c[k] = c[ls] * c[rs];
}
inline void modify (int k, int l, int r, int pos)
{
if (l == r) {c[k].getmatrix(l); return;}
int mid = l + r >> 1;
if (pos <= mid)
modify(ls, l, mid, pos);
else
modify(rs, mid + 1, r, pos);
c[k] = c[ls] * c[rs];
}
int main ()
{
scanf("%d %d", &n, &m);
fo (i, 1, n) scanf("%lld", &a[i].v);
fo (i, 1, n) scanf("%lld", &b[i].v);
fo (i, 1, n) a[i].id = b[i].id = i;
std::sort(a + 1, a + n + 1);
std::sort(b + 1, b + n + 1);
fo (i, 1, n) posa[a[i].id] = posb[b[i].id] = i;
//posa[i] 表示原序列中第 i 位在排序序列中的位置
build(1, 1, n);
fo (i, 1, n)
tmp.getmatrix(i);
fo (i, 1, m)
{
scanf("%d %d", &x, &y);
std::swap(b[posb[x]].id, b[posb[y]].id);
std::swap(posb[x], posb[y]);
//只交换马儿的标号,保证主人与马儿之间标号错排即可
x = posa[x]; y = posa[y];
fo (j, x, std::min(n, x + 2)) modify(1, 1, n, j);
fo (j, y, std::min(n, y + 2)) modify(1, 1, n, j);
printf("%lld\n", c[1].t[2][2]);
}
return 0;
}
线性的动态 dp 就讲完了,那么我们来讲一讲树上的动态 dp 吧
树上最大权独立集+动态修改,我们应该怎么搞呢?
分析静态,设 $f[u][0/1]$表示 u 点选/不选,以 u 为根的子树的最大权独立集。显然有
$$f[u][0]=\sum_{v \in son_u}max\{f[v][0], f[v][1]\}$$
$$f[u][1]=a[u] + \sum_{v \in son_u}f[v][0]$$
想想我们刚刚是怎么把静态转换成动态的——维护转移矩阵。
可是这里带 sigma 你怎么写矩阵呀,而且还有树上你怎么像线性一样搞呀?暴力往上搞退化成链怎么办啊?
用树剖就没有什么好害怕的了
用树剖将树上操作转换成序列操作,修改操作也就是在 $logn$条链上像线性一样修改转移矩阵,线性的情况我们可能就可以用线段树 $logn$维护转移矩阵了。
下面我们就只剩下一个问题了,如何写矩阵?
因为每一个点的转移只与 son 有关,不妨写一个二阶矩阵,一个点还有 heavyson 和 lightson 两种 son,我们不妨就按照这个东西来分类
记当前点为 u,记 $g_0$表示不选 u 点轻儿子对 u 的贡献,$g_1$表示选 u 点轻儿子对 u 的贡献,记 v 为 u 的重儿子。
$g_0,g_1$怎么算就不说了,对于转移方程我们有
$$f[u][0] = max\{g_0+f[v][0], g_1+f[v][1]\}$$
$$f[u][1]=a_u+g_0+f[v][0]$$
写成矩阵的形式就是源码戳这里:
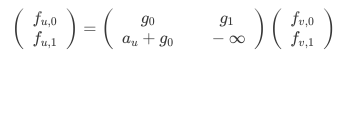
用线段树维护这个东西就行了。
等等我们是不是忘记了什么。
一条链是没问题了,但是这条链 top 的 father 的两个 g 值好像是咕咕咕的。
没有关系,每次我们跳链的时候改一改就好了,记这条链 top 的 father 是 u 点,那么这条链其实是 u 点的轻链,改一下 u 点的转移矩阵中的两个 g 值就行了。
代码:
#include<bits/stdc++.h>
#define Re register
#define fo(i, a, b) for (Re int i = (a); i <= (b); ++i)
#define fd(i, a, b) for (Re int i = (a); i >= (b); --i)
#define edge(i, u) for (Re int i = head[u], v = e[i].v; i; i = e[i].nxt, v = e[i].v)
#define pb push_back
#define F first
#define S second
#define ll long long
#define inf 1000000007
#define mp std::make_pair
#define lowbit(x) (x & -x)
#define mod 19260817
#define eps 1e-4
#define itset std::set<node>::iterator
#define lb lower_bound
#define N 300005
#define ls (k << 1)
#define rs (k << 1 | 1)
int n, m, x, y, a[N], head[N], tot, u;
struct edge {int nxt, v;}e[N << 1];
inline void addedge (int u, int v) {e[++tot] = (edge) {head[u], v}; head[u] = tot;}
int sz[N], fa[N], dfn[N], top[N], son[N], dep[N], ed[N], tim, ds[N];
ll dp[N][2];
inline void dfs1 (int u, int fat)
{
sz[u] = 1; fa[u] = fat; dep[u] = dep[fat] + 1;
edge (i, u)
{
if (v == fat) continue;
dfs1(v, u);
sz[u] += sz[v];
if (sz[son[u]] < sz[v]) son[u] = v;
}
}
inline void dfs2 (int u, int tp)
{
dfn[u] = ++tim;
ds[tim] = u;
top[u] = tp;
ed[u] = dfn[u];
if (son[u]) {dfs2(son[u], tp); ed[u] = ed[son[u]];}
edge (i, u)
{
if (v == fa[u] || v == son[u]) continue;
dfs2(v, v);
}
}
inline void dfs (int u)
{
dp[u][1] = a[u];
edge (i, u)
{
if (v == fa[u]) continue;
dfs(v);
dp[u][0] += std::max(dp[v][1], dp[v][0]);
dp[u][1] += dp[v][0];
}
}
struct matrix{
ll t[2][2];
inline void clear () {memset(t, 0, sizeof t);}
friend matrix operator * (matrix x, matrix y)
{
matrix c;
c.t[0][0] = std::max(x.t[0][0] + y.t[0][0], x.t[0][1] + y.t[1][0]);
c.t[0][1] = std::max(x.t[0][0] + y.t[0][1], x.t[0][1] + y.t[1][1]);
c.t[1][0] = std::max(x.t[1][0] + y.t[0][0], x.t[1][1] + y.t[1][0]);
c.t[1][1] = std::max(x.t[1][0] + y.t[0][1], x.t[1][1] + y.t[1][1]);
return c;
}
inline void getmatrix (int u)
{
ll g0 = 0, g1 = 0;
edge (i, u)
{
if (v == fa[u] || v == son[u]) continue;
g0 += std::max(dp[v][0], dp[v][1]);
g1 += dp[v][0];
}
t[0][0] = t[0][1] = g0;
t[1][0] = g1 + a[u]; t[1][1] = -inf;
}
}c[N << 2], b[N];
inline void build (int k, int l, int r)
{
if (l == r) {c[k].getmatrix(ds[l]); b[l] = c[k]; return;}
int mid = l + r >> 1;
build(ls, l, mid); build(rs, mid + 1, r);
c[k] = c[ls] * c[rs];
}
inline void modify (int k, int l, int r, int pos)
{
if (l == r) {
c[k] = b[l]; return;
}
int mid = l + r >> 1;
if (pos <= mid)
modify(ls, l, mid, pos);
else
modify(rs, mid + 1, r, pos);
c[k] = c[ls] * c[rs];
}
inline matrix query (int k, int l, int r, int L, int R)
{
if (L <= l && r <= R) return c[k];
int mid = l + r >> 1;
if (L <= mid && mid < R) return query(ls, l, mid, L, R) * query(rs, mid + 1, r, L, R);
else if (L <= mid) return query(ls, l, mid, L, R);
else if (mid < R) return query(rs, mid + 1, r, L, R);
}
inline void work (int x, int y)
{
b[dfn[x]].t[1][0] += y - a[x]; a[x] = y;//修改当前点的权值
while (x) //往上更新每条链 top 的 fa 的 g 值
{
matrix m1, m2;
m1 = query(1, 1, n, dfn[top[x]], ed[x]);//获取原来的 g[fa[top[u]]][0/1]
modify(1, 1, n, dfn[x]);//修改链上的所有矩阵
m2 = query(1, 1, n, dfn[top[x]], ed[x]);//获取现在的 g[fa[top[u]]][0/1]
x = fa[top[x]];
if (!x) break;
b[dfn[x]].t[0][0] += std::max(m2.t[0][0], m2.t[1][0]) - std::max(m1.t[0][0], m1.t[1][0]);
b[dfn[x]].t[0][1] = b[dfn[x]].t[0][0];
b[dfn[x]].t[1][0] += m2.t[0][0] - m1.t[0][0];
}
}
int main ()
{
scanf("%d %d", &n, &m);
fo (i, 1, n) scanf("%d", &a[i]);
fo (i, 2, n)
{
scanf("%d %d", &x, &y);
addedge(x, y); addedge(y, x);
}
dfs1(1, 0); dfs2(1, 1); dfs(1);
build(1, 1, n);
fo (i, 1, m)
{
scanf("%d %d", &x, &y);
work(x, y);
matrix ans = query(1, 1, n, 1, ed[1]);
printf("%lld\n", std::max(ans.t[0][0], ans.t[1][0]));
}
return 0;
}
我们看回今年 D2T3:传送门酱 qwq
这道题是动态树上最小权点覆盖,乍一看好像不一样,其实想想就知道了最小权点覆盖和最大权独立集就是一个互补关系,前者是每条边至少选一个点,点权最小,后者则是每条边至多选一个点,点权最大,两者相加不就是全集了吗?
然后知道这个转换你就乐滋滋了。强制选赋值为正无穷,强制不选赋值为负无穷,然后就是动态 dp 板子了 (注意一下 long long)。
代码:
#include<bits/stdc++.h>
#define Re register
#define fo(i, a, b) for (Re int i = (a); i <= (b); ++i)
#define fd(i, a, b) for (Re int i = (a); i >= (b); --i)
#define edge(i, u) for (Re int i = head[u], v = e[i].v; i; i = e[i].nxt, v = e[i].v)
#define pb push_back
#define F first
#define S second
#define ll long long
#define inf 10000000000007
#define mp std::make_pair
#define lowbit(x) (x & -x)
#define mod 19260817
#define eps 1e-4
#define itset std::set<node>::iterator
#define lb lower_bound
#define N 300005
#define ls (k << 1)
#define rs (k << 1 | 1)
#define int long long
int n, m, x, y, a[N], head[N], tot, u;
struct edge {int nxt, v;}e[N << 1];
inline void addedge (int u, int v) {e[++tot] = (edge) {head[u], v}; head[u] = tot;}
int sz[N], fa[N], dfn[N], top[N], son[N], dep[N], ed[N], tim, ds[N];
ll dp[N][2];
inline void dfs1 (int u, int fat)
{
sz[u] = 1; fa[u] = fat; dep[u] = dep[fat] + 1;
edge (i, u)
{
if (v == fat) continue;
dfs1(v, u);
sz[u] += sz[v];
if (sz[son[u]] < sz[v]) son[u] = v;
}
}
inline void dfs2 (int u, int tp)
{
dfn[u] = ++tim;
ds[tim] = u;
top[u] = tp;
ed[u] = dfn[u];
if (son[u]) {dfs2(son[u], tp); ed[u] = ed[son[u]];}
edge (i, u)
{
if (v == fa[u] || v == son[u]) continue;
dfs2(v, v);
}
}
inline void dfs (int u)
{
dp[u][1] = a[u];
edge (i, u)
{
if (v == fa[u]) continue;
dfs(v);
dp[u][0] += std::max(dp[v][1], dp[v][0]);
dp[u][1] += dp[v][0];
}
}
struct matrix{
ll t[2][2];
inline void clear () {memset(t, 0, sizeof t);}
friend matrix operator * (matrix x, matrix y)
{
matrix c;
c.t[0][0] = std::max(x.t[0][0] + y.t[0][0], x.t[0][1] + y.t[1][0]);
c.t[0][1] = std::max(x.t[0][0] + y.t[0][1], x.t[0][1] + y.t[1][1]);
c.t[1][0] = std::max(x.t[1][0] + y.t[0][0], x.t[1][1] + y.t[1][0]);
c.t[1][1] = std::max(x.t[1][0] + y.t[0][1], x.t[1][1] + y.t[1][1]);
return c;
}
inline void getmatrix (int u)
{
ll g0 = 0, g1 = 0;
edge (i, u)
{
if (v == fa[u] || v == son[u]) continue;
g0 += std::max(dp[v][0], dp[v][1]);
g1 += dp[v][0];
}
t[0][0] = t[0][1] = g0;
t[1][0] = g1 + a[u]; t[1][1] = -inf;
}
}c[N << 2], b[N];
inline void build (int k, int l, int r)
{
if (l == r) {c[k].getmatrix(ds[l]); b[l] = c[k]; return;}
int mid = l + r >> 1;
build(ls, l, mid); build(rs, mid + 1, r);
c[k] = c[ls] * c[rs];
}
inline void modify (int k, int l, int r, int pos)
{
if (l == r) {
c[k] = b[l]; return;
}
int mid = l + r >> 1;
if (pos <= mid)
modify(ls, l, mid, pos);
else
modify(rs, mid + 1, r, pos);
c[k] = c[ls] * c[rs];
}
inline matrix query (int k, int l, int r, int L, int R)
{
if (L <= l && r <= R) return c[k];
int mid = l + r >> 1;
if (L <= mid && mid < R) return query(ls, l, mid, L, R) * query(rs, mid + 1, r, L, R);
else if (L <= mid) return query(ls, l, mid, L, R);
else if (mid < R) return query(rs, mid + 1, r, L, R);
}
inline void work (int x, int y)
{
b[dfn[x]].t[1][0] += y - a[x]; a[x] = y;
while (x)
{
matrix m1, m2;
m1 = query(1, 1, n, dfn[top[x]], ed[x]);
modify(1, 1, n, dfn[x]);
m2 = query(1, 1, n, dfn[top[x]], ed[x]);
x = fa[top[x]];
if (!x) break;
b[dfn[x]].t[0][0] += std::max(m2.t[0][0], m2.t[1][0]) - std::max(m1.t[0][0], m1.t[1][0]);
b[dfn[x]].t[0][1] = b[dfn[x]].t[0][0];
b[dfn[x]].t[1][0] += m2.t[0][0] - m1.t[0][0];
}
}
main ()
{
scanf("%lld %lld", &n, &m);
char ch = getchar();
if (ch != 'A' && ch != 'B' && ch != 'C') ch = getchar();
scanf("%lld", &x);
int sum = 0;
fo (i, 1, n) {scanf("%lld", &a[i]); sum += a[i];}
fo (i, 2, n)
{
scanf("%lld %lld", &x, &y);
addedge(x, y); addedge(y, x);
}
dfs1(1, 0); dfs2(1, 1); dfs(1);
build(1, 1, n);
fo (i, 1, m)
{
int pa, pb;
scanf("%lld %lld %lld %lld", &pa, &x, &pb, &y);
int tp1 = a[pa], tp2 = a[pb];
work(pa, tp1 + (x ? -inf : inf));
work(pb, tp2 + (y ? -inf : inf));
matrix ans = query(1, 1, n, 1, ed[1]);
int now = sum - std::max(ans.t[0][0], ans.t[1][0]);
x = !x; y = !y;
now += (x + y) * inf;
if (now > inf)
printf("-1\n");
else
printf("%lld\n", now);
work(pa, tp1);
work(pb, tp2);
}
return 0;
}
0 条评论