题目分析

先将网格图红白染色（你问为什么不是黑白？因为我在草稿纸上画图时发现把黑色格子改成红色是不可能的……）。

然后将与蓝色线相邻的红色格子改成黑色，相邻的白色格子改成蓝色。

大概长这样（灵魂画手 litble 再现江湖！）

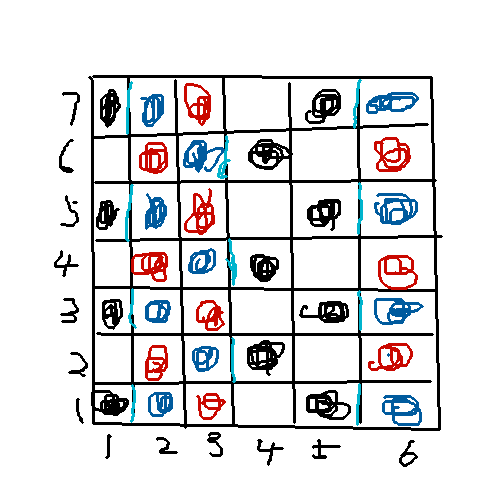
这样你会发现：

1. 整张图黑格子与红格不相邻，蓝格子和白格子不相邻。

2. 任何一个特殊图形，是一对相邻的黑格子和蓝格子，加上与它们连通的一个白格子和一个蓝格子。

思考建图，由这些格子之间的依赖关系可以猜到是个最小割。

假设有一个蓝格子 A 和与其相邻的一个黑格子 B，与他们直接相连的白色和红色格子都有方块，那么我们需要选择下列三种操作的至少一种：

1. 删掉所有白格子

2. 删掉所有红格子

3. 删掉 A 和 B 其中之一

因此得到建图：S 像所有红格子连一条流量为红格子费用的边，红格子向相邻有方块的蓝格子连一条流量为 inf 的边，蓝格子向相邻黑格子连一条流量为 min(蓝格子费用，黑格子费用）的边，黑格子向相邻白格子连一条流量为 inf 的边，白格子向 T 连一条流量为白格子费用的边。

最小割即为答案。

代码

#include<bits/stdc++.h>
using namespace std;
#define RI register int
int read() {
    int q=0;char ch=' ';
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9') q=q*10+ch-'0',ch=getchar();
    return q;
}
typedef long long LL;
const int N=100010,inf=0x3f3f3f3f;
int n,m,K,cnt,S,T,ans,tot=1;
map<LL,int> mp;
int X[N],Y[N],Z[N],col[N];
int lev[N],q[N],h[N<<3],ne[N<<3],flow[N<<3],to[N<<3];
int mvx[5]={1,-1,0,0},mvy[5]={0,0,1,-1};

LL id(LL x,LL y) {return (x-1)*m+y;}
void add(int x,int y,int z) {
    to[++tot]=y,ne[tot]=h[x],h[x]=tot,flow[tot]=z;
    to[++tot]=x,ne[tot]=h[y],h[y]=tot,flow[tot]=0;
}
int dfs(int x,int liu) {
    if(x==T) return liu;
    int sum=0;
    for(RI i=h[x];i;i=ne[i])
        if(flow[i]>0&&lev[to[i]]==lev[x]+1) {
            int kl=dfs(to[i],min(flow[i],liu-sum));
            sum+=kl,flow[i]-=kl,flow[i^1]+=kl;
            if(sum==liu) return sum;
        }
    if(!sum) lev[x]=-1;
    return sum;
}
int bfs() {
    for(RI i=1;i<=cnt;++i) lev[i]=0;
    int he=1,ta=1;q[1]=S,lev[S]=1;
    while(he<=ta) {
        int x=q[he];++he;
        if(x==T) return 1;
        for(RI i=h[x];i;i=ne[i])
            if(flow[i]>0&&!lev[to[i]])
                lev[to[i]]=lev[x]+1,q[++ta]=to[i];
    }
    return 0;
}

void work_black(int x,int y,int k1) {
    for(RI i=0;i<4;++i) {
        int tx=x+mvx[i],ty=y+mvy[i];
        if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&mp[id(tx,ty)]) {
            int k2=mp[id(tx,ty)];
            if(col[k2]==3) add(k2,k1,min(Z[k1],Z[k2]));
            else add(k1,k2,inf);
        }
    }
}
void work_blue(int x,int y,int k1) {
    for(RI i=0;i<4;++i) {
        int tx=x+mvx[i],ty=y+mvy[i];
        if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&mp[id(tx,ty)]) {
            int k2=mp[id(tx,ty)];
            if(col[k2]!=2) add(k2,k1,inf);
        }
    }
}
int main()
{
    n=read(),m=read(),K=read();
    for(RI i=1;i<=K;++i)
        X[i]=read(),Y[i]=read(),Z[i]=read(),mp[id(X[i],Y[i])]=++cnt;
    S=++cnt,T=++cnt;
    for(RI i=1;i<=K;++i) {
        if(X[i]%4==1) col[i]=(Y[i]&1?2:4);
        else if(X[i]%4==2) col[i]=(Y[i]&1?3:1);
        else if(X[i]%4==3) col[i]=(Y[i]&1?1:3);
        else col[i]=(Y[i]&1?4:2);
    }
    for(RI i=1;i<=K;++i) {
        if(col[i]==2) work_black(X[i],Y[i],i);
        else if(col[i]==3) work_blue(X[i],Y[i],i);
        else if(col[i]==1) add(S,i,Z[i]);
        else add(i,T,Z[i]);
    }
    while(bfs()) ans+=dfs(S,inf);
    printf("%d\n",ans);
    return 0;
}