最小圆覆盖 luoguP1742

给定 $n$个点，求一个最小的圆包围所有的点。

随机增量法

定理 1：如果点 $p$不在集合 $S$的最小覆盖圆内，则 $p$一定在 $S\cup{p}$的最小覆盖圆上。

根据这个定理，我们可以分三次确定前 $i$个点的最小覆盖圆。

• 1. 令前 $i-1$个点的最小覆盖圆为 $C$
• 2. 如果第 $i$个点在 $C$内，则前 $i$个点的最小覆盖圆也是 $C$
• 3. 如果不在，那么第 $i$个点一定在前 $i$个点的最小覆盖圆上，接着确定前 $i-1$个点中还有哪两个在最小覆盖圆上。因此，设当前圆心为 $P_i$，半径为 0，做固定了第 $i$个点的前 $i$个点的最小圆覆盖。
• 4. 固定了一个点：不停地在范围内找到第一个不在当前最小圆上的点 $P_j$，设当前圆心为 $(P_i+P_j)/2$，半径为 $\frac{1}{2}|P_iP_j|$，做固定了两个点的，前 $j$个点外加第 $i$个点的最小圆覆盖。
• 5. 固定了两个点：不停地在范围内找到第一个不在当前最小圆上的点 $P_k$，设当前圆为 $P_i,P_j,P_k$的外接圆。

写成伪代码的形式非常简单：

圆 C;
for(i=1 to n)
{
    if(P[i] 不在 C 内)
    {
        C = {P[i], 0};
        for(j=1 to i-1)
        {
            if(P[j] 不在 C 内)
            {
                C = {0.5*(P[i]+P[j]), 0.5*dist(P[i], P[j])};
                for(k=1 to j-1)
                {
                    if(P[k] 不在 C 内)
                    {
                        C = 外接圆 (P[i], P[j], P[k]);
                    }
                }
            }
        }
    }
}

只需要三个模式完全相同的 for 循环就可以搞定。

但是对于这个算法，还有三个地方需要明确：如何求外接圆，以及复杂度是多少。

外接圆

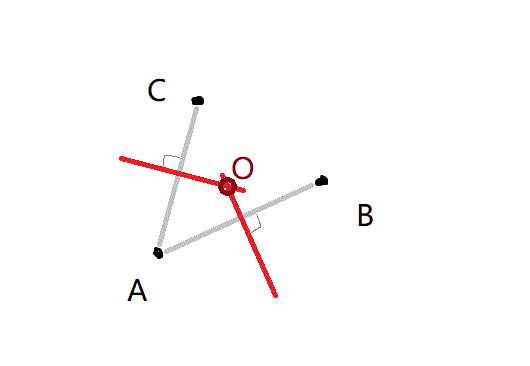
可以使用初中的中垂线法。设三个不共线点为 $A,B,C$，那么我们可以求 $AB,AC$中垂线的交点。

以下我们需要四个工具去完成这个任务：

• 求两个向量的中点
• 将一个向量旋转 90 度
• 用直线上某一点坐标和其方向向量表示一条直线
• 求两条直线的交点

第一个任务，求两个向量的中点，将横纵坐标相加除以二即可。

第二个任务，将一个向量旋转 90 度，如果是顺时针旋转，即 $(x,y)$变成 $(y,-x)$

第三个任务，已经说白了，两个向量就可以表示一条直线。

第四个任务稍微有一点复杂，但是不是很复杂。众所周知，二维向量的叉积可以表示两向量所形成的平行四边形的有向面积。我们可以利用这一点解决直线交点的问题。

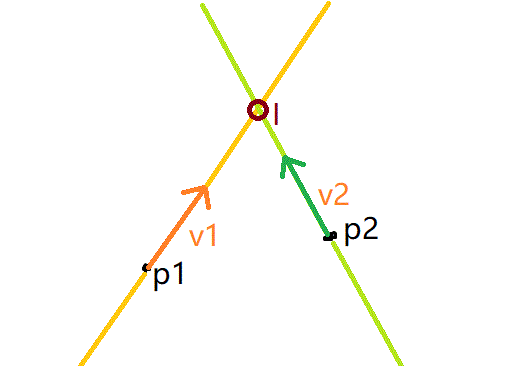
用 $p_1,v_1$表示 $I$，即：$I=p_1+tv_1$

又 $I$在绿色直线上，所以又向量 $(I-p_2)$和 $v_2$构成的平行四边形面积为 $0$，即 $(p_1+tv_1-p_2)\times p_2 = 0$

解方程得，$t=\frac{(p_2-p_1)\times p_2}{v_1\times p_2}$，交点 $I$就是 $p_1+tv_1$

利用上述四个工具，我们可以求出三个点的外接圆。

复杂度证明

由于一堆点最多只有 $3$个点确定了最小覆盖圆，因此 $n$个点中每个点参与确定最小覆盖圆的概率不大于 $\frac{3}{n}$

所以，每一层循环在第 $i$个点处调用下一层的概率不大于 $\frac{3}{i}$

那么设算法的三个循环的复杂度分别为 $T_1(n),T_2(n),T_3(n)$，则有：

$$\begin{aligned}T_1(n) & = O(n) + \sum_{i=1}^{n}{\frac{3}{i}T_2(i)}\\ T_2(n) & = O(n) + \sum_{i=1}^{n}{\frac{3}{i}T_3(i)}\\ T_3(n) & = O(n)\end{aligned}$$

不难解得，$T_1(n)=T_2(n)=T_3(n)=O(n)$

代码

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>

using namespace std;

struct vec
{
    double x, y;
    vec (const double& x0 = 0, const double& y0 = 0) : x(x0), y(y0) {}
    vec operator + (const vec& t) const {return vec(x+t.x, y+t.y);}
    vec operator - (const vec& t) const {return vec(x-t.x, y-t.y);}
    vec operator * (const double& t) const {return vec(x*t, y*t);}
    vec operator / (const double& t) const {return vec(x/t, y/t);}
    const double len2 () const {return x*x + y*y;}
    const double len () const {return sqrt(len2());}
    vec norm() const {return *this/len();}
    vec rotate_90_c () {return vec(y, -x);}
};

double dot(const vec& a, const vec& b) {return a.x*b.x + a.y*b.y;}
double crs(const vec& a, const vec& b) {return a.x*b.y - a.y*b.x;}

vec lin_lin_int(const vec& p0, const vec& v0, const vec& p1, const vec& v1)
{
    double t = crs(p1-p0, v1) / crs(v0, v1);
    return p0 + v0 * t;
}

vec circle(const vec& a, const vec& b, const vec& c)
{
    return lin_lin_int((a+b)/2, (b-a).rotate_90_c(), (a+c)/2, (c-a).rotate_90_c());
}

int n;
vec pot[100005];

int main()
{
    scanf("%d", &n);
    for(int i=1; i<=n; i++) scanf("%lf%lf", &pot[i].x, &pot[i].y);
    random_shuffle(pot+1, pot+n+1);
    vec o;
    double r2 = 0;
    for(int i=1; i<=n; i++)
    {
        if((pot[i]-o).len2() > r2)
        {
            o = pot[i], r2 = 0;
            for(int j=1; j<i; j++)
            {
                if((pot[j]-o).len2() > r2)
                {
                    o = (pot[i]+pot[j])/2, r2 = (pot[j]-o).len2();
                    for(int k=1; k<j; k++)
                    {
                        if((pot[k]-o).len2() > r2)
                        {
                            o = circle(pot[i], pot[j], pot[k]), r2 = (pot[k]-o).len2();
                        }
                    }
                }
            }
        }
    }
    printf("%.10lf\n%.10lf %.10lf\n", sqrt(r2), o.x, o.y);
    return 0;
}