什么是圆的反演

给定一个圆心为 $C$半径为 $R$的圆。对于在圆心 $C$同侧的两个点 $A$和 $A’$，若 $|CA|*|CA’|=R^2$，则说 $A$和 $A’$互为关于圆 $C$的反演点。

在经过一次反演后，圆 $C$内的点都到了圆外，圆外的点都到了圆内。

$C$被称为反演中心，$R$被称为反演半径。

圆的反演有什么用

圆的反演的性质：

过反演中心的圆，反形是不过反演中心的相交直线。不过反演中心的圆，反形还是圆。反演中心的不过反演中心的直线，反形是反演中心的圆。

我们都知道，圆的公切圆很不好求，但是公切线（相对）很好求。所以如果我想求两圆过定点的公切圆，只要在以定点为反演中心做反演后，求两圆的公切线，再把公切线反演回去就好了。

具体实现

反演一个圆

如图所示，$C_1$是原图形，$C_2$是反形，$O$是反演中心，$R$是反演半径，$A_1$与 $A_2$互为反演点，$B_1$与 $B_2$互为反演点。

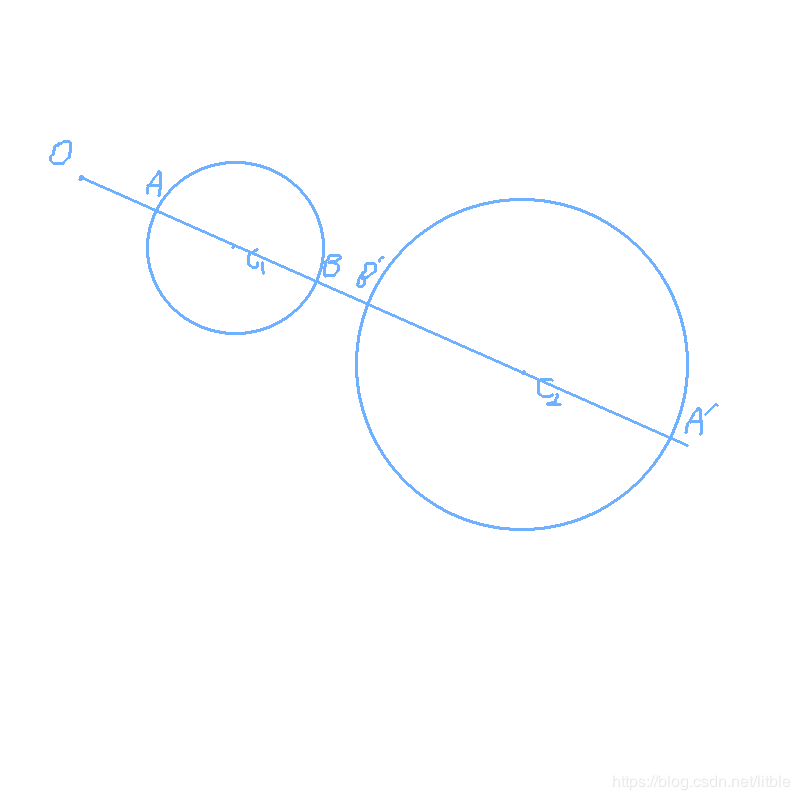
不难发现

$$|OA|*|OA’|=(|OC_1|-r_1)(|OC_2|+r_2)=R^2$$

$$|OB|*|OB’|=(|OC_1|+r_1)(|OC_2|-r_2)=R^2$$

所以

$$r_2=\frac{R^2}{2}(\frac{1}{|OC_1|-r_1}-\frac{1}{|OC_1|+r_1})$$

$$|OC_2|=\frac{R^2}{2}(\frac{1}{|OC_1|-r_1}+\frac{1}{|OC_1|+r_1})$$

然后就不难求出反形了。

反演一条直线

作反演中心到该直线的垂线，由于垂足是直线上离反演中心最近的点，所以在反演后，它也是反形（圆）上离反演中心最远的点。将垂足的反演点求出后，就不难求出反形的半径和圆心了。

其他

有的反形的公切线是不能转化为公切圆的，因为可能转化后会是半径为无穷大的公切圆，那么也就是反形的公切线若过反演中心，就不能转化为公切圆。

代码

#include <bits/stdc++.h>
using namespace std;
#define RI register int
typedef double db;
const db R=1,eps=1e-9;
int T,cnt;
struct point{db x,y;}P;
point operator + (point A,point B) {return (point){A.x+B.x,A.y+B.y};}
point operator - (point A,point B) {return (point){A.x-B.x,A.y-B.y};}
point operator / (point A,db B) {return (point){A.x/B,A.y/B};}
point operator * (point A,db B) {return (point){A.x*B,A.y*B};}
db operator & (point A,point B) {return A.x*B.x+A.y*B.y;}
db operator * (point A,point B) {return A.x*B.y-A.y*B.x;}
struct circle{point o;db r;}c1,c2,ans[6];

#define sqr(x) ((x)*(x))
db dist(point A,point B) {return sqrt(sqr(A.x-B.x)+sqr(A.y-B.y));}
db mo(point A) {return sqrt(sqr(A.x)+sqr(A.y));}
point rot(point A,db ang)
    {return (point){A.x*cos(ang)-A.y*sin(ang),A.x*sin(ang)+A.y*cos(ang)};}
circle inversion_circle(circle c) {//反演一个圆
    db d=dist(c.o,P),k1=1.0/(d-c.r),k2=1.0/(d+c.r);
    circle re;point v=(c.o-P)/d;
    re.r=R*R/2.0*(k1-k2);
    re.o=P+v*(R*R/2.0*(k1+k2));
    return re;
}
void inversion_line(point A,point B) {//反演一条直线
    point v=B-A,H=A+v*(((P-A)&v)/sqr(mo(v)));
    ++cnt;point kv=(H-P)*sqr(R/dist(H,P));
    ans[cnt].o=P+kv*0.5,ans[cnt].r=mo(kv)/2.0;
}
void work() {
    c1=inversion_circle(c1),c2=inversion_circle(c2);
    if(c1.r<c2.r) swap(c1,c2);

    //求外公切线: 小圆的圆心往大圆与切线垂直的半径做垂线
    point v=c2.o-c1.o;
    db d=dist(c1.o,c2.o),a1=atan2(v.y,v.x),a2=acos((c1.r-c2.r)/d);
    point k1=(point){c1.o.x+cos(a1+a2)*c1.r,c1.o.y+sin(a1+a2)*c1.r};
    point k2=(point){c2.o.x+cos(a1+a2)*c2.r,c2.o.y+sin(a1+a2)*c2.r};
    if(fabs((P-k1)*(k2-k1))>eps) inversion_line(k1,k2);
    point k3=(point){c1.o.x+cos(a1-a2)*c1.r,c1.o.y+sin(a1-a2)*c1.r};
    point k4=(point){c2.o.x+cos(a1-a2)*c2.r,c2.o.y+sin(a1-a2)*c2.r};
    if(fabs((P-k3)*(k4-k3))>eps) inversion_line(k3,k4);

    //求内公切线：先求出两圆内公切线交点，然后用求点到圆的切线的方法求
    db kd1=d*c1.r/(c1.r+c2.r),kd2=d*c2.r/(c1.r+c2.r);
    point tangent_intersection=c1.o+(c2.o-c1.o)*(kd1/d);
    db a3=asin(c1.r/dist(tangent_intersection,c1.o));
    point v0=c1.o-tangent_intersection;
    point v1=rot(v0,a3),v2=rot(v0,-a3);
    v1=v1/mo(v1),v2=v2/mo(v2);
    point k5=tangent_intersection+v1*kd1,k6=tangent_intersection-v1*kd2;
    if(fabs((P-k5)*(k6-k5))>eps) inversion_line(k5,k6);
    point k7=tangent_intersection+v2*kd1,k8=tangent_intersection-v2*kd2;
    if(fabs((P-k7)*(k8-k7))>eps) inversion_line(k7,k8);
}
int main()
{
    scanf("%d",&T);
    while(T--) {
        scanf("%lf%lf%lf",&c1.o.x,&c1.o.y,&c1.r);
        scanf("%lf%lf%lf",&c2.o.x,&c2.o.y,&c2.r);
        scanf("%lf%lf",&P.x,&P.y);
        cnt=0,work();
        printf("%d\n",cnt);
        for(RI i=1;i<=cnt;++i)
            printf("%.8f %.8f %.8f\n",ans[i].o.x,ans[i].o.y,ans[i].r);
    }
    return 0;
}