【题解】[HNOI2012] 射箭 半平面交 BZOJ – 2732

题目戳我_(:зゝ∠)_

这题着实恶心到我了。。。

主要是 HZWER 的代码写错了。。。他的代码很迷，连 eps 都没用上。。。

设抛物线方程：$y = a x ^ 2 + b x$

每个靶子 $(x, y _ 1, y _ 2)$就是一个限制：

$$y _ 1 \leq x ^ 2 a + x b \leq y _ 2$$
$$\frac {y _ 1} x \leq x a + b \leq \frac {y _ 2} x$$

这个限制画到平面上就是这样一块区域（横轴代表 $a$，纵轴代表 $b$，图中的不等式为 $2 \leq 0.5 a + b \leq 5$）：

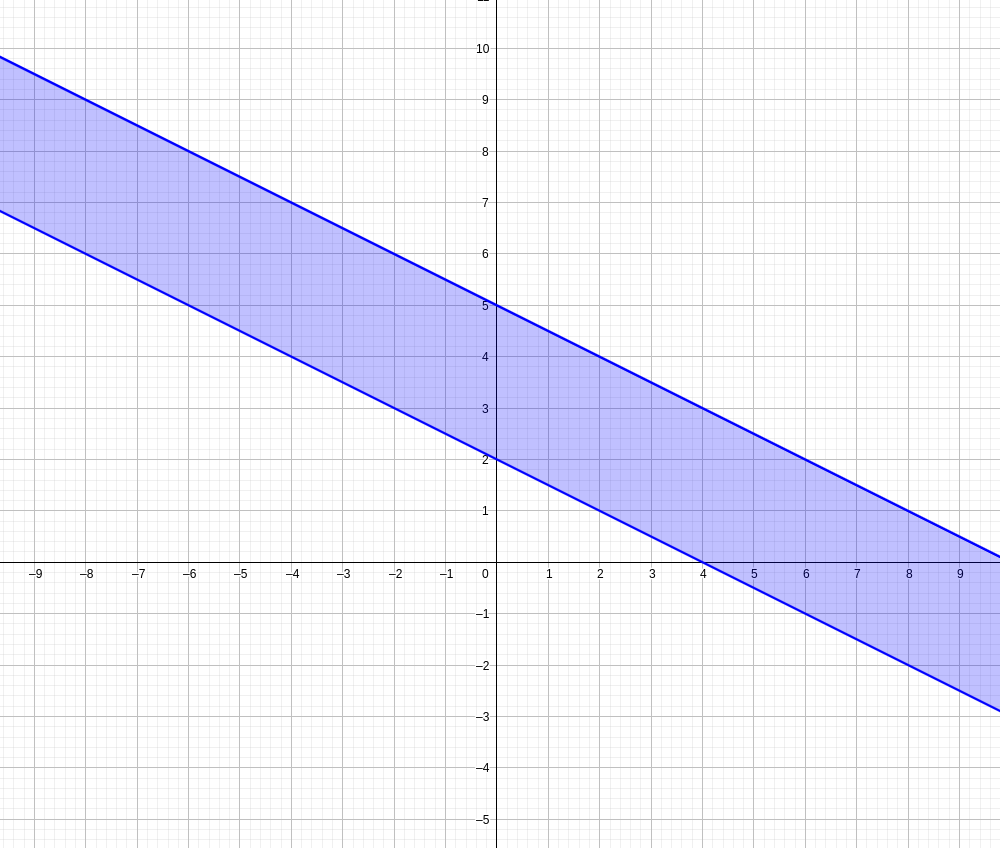
很多个这样的区域取交就是能一次穿透这些靶子的抛物线的 $(a, b)$取值范围

如果无交集则无解，否则有解

如果一遍扫过去得动态半平面交似乎太麻烦了，可以先把半平面排好序，然后二分答案，按排好序的顺序选出这些半平面 $O(n)$判断，复杂度也是 $O(n log _ 2 n)$的

然后细节很多，而且坐标范围 $10 ^ 9$精度要求较高

细节如下：

• 你不是卢本伟你没开挂，箭不能反重力也不能穿地，因此你要限制抛物线开口向下
• 你不是大力哥你不能大力出奇迹，不能打一条直线出去你打的是抛物线啊，总之你得限制 $a, b > 0$
• 精度要求较高，最好把向量都单位化，免得一乘起来就 $10 ^ {30}$了。。。而且 $eps$取 $10 ^ {-14}$比较合适
• 半平面交时相邻的两条直线的 $\Delta \theta$得 $\leq \frac \pi 2$，不然会出现奇妙♂的事情

总之我写这题大概就是这个状态：

写完了：

好吧不多说了上代码吧

#include <bits/stdc++.h>

#define NS (100010)
#define inf (1e11)
#define eps (1e-14)
#define dCmp(a, b) ((a) - (b) < eps && (a) - (b) > -eps)

using namespace std;

const double PI = acos(-1);

struct vec
{
    double x, y;
    vec() {x = y = 0;}
    vec(double a, double b) {x = a, y = b;}
    vec operator + (const vec oth) const
    {
        return vec(x + oth.x, y + oth.y);
    }
    vec operator - (const vec oth) const
    {
        return vec(x - oth.x, y - oth.y);
    }
    vec operator * (const double d) const {return vec(x * d, y * d);}
    double crs(const vec oth) {return x * oth.y - y * oth.x;}
};

struct ray
{
    vec u, v; int id; double angle;
    void cal() {angle = atan2(v.y, v.x);}
    vec ins(const ray oth)
    {
        return u + v * ((oth.u - u).crs(oth.v) / v.crs(oth.v));
    }
} L[NS << 1], P[NS << 1], Q[NS << 1];

bool anCmp(ray a, ray b)
{
    if (dCmp(a.angle, b.angle)) return a.v.crs(b.u - a.u) > 0;
    return a.angle < b.angle;
}

int n, rc;

#define jud(a, b, x) (((a).ins(b) - (x).u).crs((x).v) > 0)

bool check(int id)
{
    int m = 0; P[0].angle = 233;
    for (int i = 1; i <= rc; i += 1)
        if (L[i].id <= id)
        {
            if (dCmp(L[i].angle, P[m].angle)) P[m] = L[i];
            else P[++m] = L[i];
        }
    int l = 1, r = 1;
    Q[r++] = P[1], Q[r++] = P[2];
    for (int i = 3; i <= m; i += 1)
    {
        while (r - l > 1 && jud(Q[r - 2], Q[r - 1], P[i])) r--;
        while (r - l > 1 && jud(Q[l + 1], Q[l], P[i])) l++;
        Q[r++] = P[i];
    }
    while (r - l > 1 && jud(Q[r - 2], Q[r - 1], Q[l])) r--;
    while (r - l > 1 && jud(Q[l + 1], Q[l], Q[r - 1])) l++;
    return r - l > 2;
}

int main(int argc, char const* argv[])
{
    scanf("%d", &n);
    L[++rc].u = vec(-inf, eps), L[rc].v = vec(1, 0), L[rc].cal();
    L[++rc].u = vec(-eps, eps), L[rc].v = vec(0, 1), L[rc].cal();
    L[++rc].u = vec(-eps, inf), L[rc].v = vec(-1, 0), L[rc].cal();
    L[++rc].u = vec(-inf, inf), L[rc].v = vec(0, -1), L[rc].cal();
    for (int i = 1; i <= n; i += 1)
    {
        double x, y1, y2;
        scanf("%lf%lf%lf", &x, &y1, &y2);
        L[++rc].u = vec(0, y2 / x), L[rc].v = vec(-1, x);
        L[rc].id = i, L[rc].cal();
        L[++rc].u = vec(0, y1 / x), L[rc].v = vec(1, -x);
        L[rc].id = i, L[rc].cal();
    }
    sort(L + 1, L + 1 + rc, anCmp);
    int l = 1, r = n, mid;
    while (l < r)
    {
        mid = (l + r + 1) >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    printf("%d\n", l);
    return 0;
}