题意：给定一个长度为 n 的序列，m 个询问 [a,b]，求 [a,b] 间最大子段和的开头和结尾。

思路：用线段树解答，每个节点保存对应段的最大前缀的结尾位置，最大后缀的开头位置，最大子段的开头结尾位置。询问时将 [a,b] 间的线段数中的区间从左到右依次取出，保存为约 log₂(b-a) 个子段，求这 log₂(b-a) 个区间所构成的最大子段和。

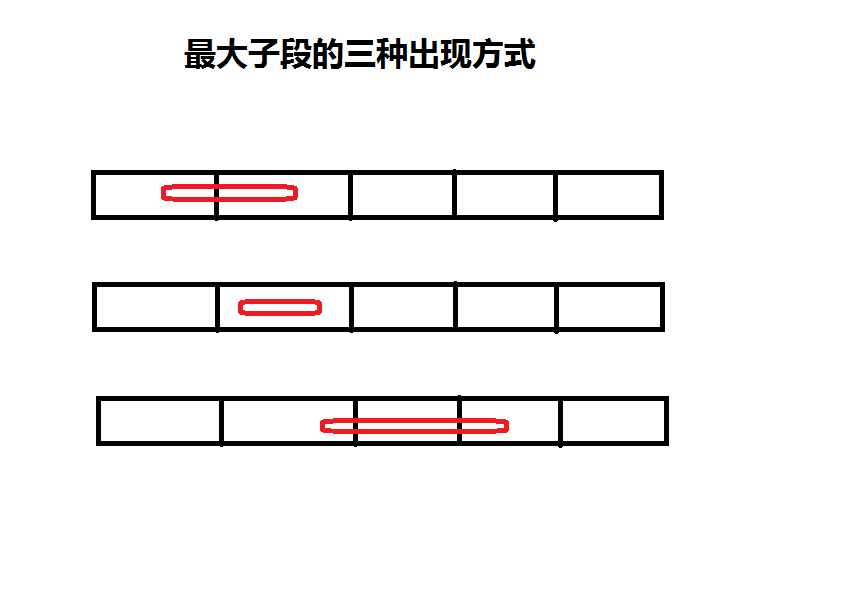
由于最大子段在这些区间中只有如下三种可能性：

其中红色部分为最大子段。

显然最大子段只可能包括 1. 某个区间 A 的最大后缀、某个区间 B 的最大前缀、和这两个区间中的所有区间（可以没有）。或者 2. 某个区间的最大子段。所以可以枚举情况 2（即图中情况 2），并用 O(N)（即原题的 O(log₂n)）求出情况 1（即图中情况 1、3）最大子段。取两者最大值。

然而，不知为何，这个程序评测总是 WA，对拍 10000 组随机、极限、手写数据都没问题。发现错误请赶快来裱我。

#include 
#include 
#include 

#define MX 500006

using namespace std;

typedef struct nd
{
    int l,r;
    int pre,suf,jotl,jotr;
} nod;

typedef struct sege
{
    int l,r;
} seg;

nod tree[MX*4];
long long psum[MX],src[MX];
int m,n;

int input()
{
    memset(src,0,sizeof(src));
    if(!(~scanf("%d%d",&n,&m)))return 0;
    for(int i=1; i<=n; i++)scanf("%lld",&src[i]);
    return 1;
}

void init()
{
    psum[0]=0;
    for(int i=1; ipsum[b.r]-psum[b.l-1])?a:b;
    else if(a.l!=b.l)return (a.l<b.l)?a:b;
    else return a.r<b.r?a:b;
}

void build(int node,int l,int r)
{
    if(l==r)tree[node].l=l,tree[node].r=r,tree[node].jotl=l,tree[node].jotr=r,tree[node].pre=l,tree[node].suf=l;
    else
    {
        build(node*2,l,(l+r)/2);
        build(node*2+1,(l+r)/2+1,r);
        seg a,b,c,as;
        a.l=tree[node*2].jotl,a.r=tree[node*2].jotr;
        b.l=tree[node*2+1].jotl,b.r=tree[node*2+1].jotr;
        c.l=tree[node*2].suf,c.r=tree[node*2+1].pre;
        as=better(better(a,b),c);
        tree[node].jotl=as.l,tree[node].jotr=as.r;

        a.l=tree[node*2].l,a.r=tree[node*2].pre;
        b.l=tree[node*2].l,b.r=tree[node*2+1].pre;
        as=better(a,b);
        tree[node].pre=as.r;

        a.l=tree[node*2].suf,a.r=tree[node*2+1].r;
        b.l=tree[node*2+1].suf,b.r=tree[node*2+1].r;
        as=better(a,b);
        tree[node].suf=as.l;

        tree[node].l=l,tree[node].r=r;
    }
}

int ans[MX*4],anum;

long long getsum(seg a)
{
    if(a.l==0&&a.r==0)return -9999999999999999;
    return psum[a.r]-psum[a.l-1];
}

seg getblc(int i,int j)
{
    seg blc;
    if(i==j)blc.l=tree[i].jotl,blc.r=tree[i].jotr;
    else blc.l=tree[i].suf,blc.r=tree[j].pre;
    return blc;
}

int lst[MX];

seg getmax()
{
    seg now,mx1,mx2,mx3;
    mx1.l=mx2.l=mx3.l=0;
    mx1.r=mx2.r=mx3.r=0;
    for(int i=1;i<=anum;i++)lst[i]=i;
    for(int i=2;i<=anum-1;i++)
    {
        now=better(getblc(ans[i-1],ans[i+1]),getblc(ans[max(lst[i-1]-1,1)],ans[i+1]));
        mx1=better(mx1,now);
        if(getsum(now)!=getsum(getblc(ans[i-1],ans[i+1])))lst[i]=lst[i-1];
    }
    for(int i=1; i<=anum; i++)mx2=better(mx2,getblc(ans[i],ans[i]));
    for(int i=1;i<=anum-1;i++)mx3=better(mx3,getblc(ans[i],ans[i+1]));
    return better(better(mx1,mx2),mx3);
}

void query(int node,int ql,int qr)
{
    int l=tree[node].l,r=tree[node].r;
    if(ql<=l&&rr||l>qr)return;
    else
    {
        query(node*2,ql,qr);
        query(node*2+1,ql,qr);
    }
}

int main()
{
    seg tmp;
    int l,r,ks=0;
    while(input())
    {
        ks++;
        printf("Case %d:\n",ks);
        init();
        build(1,1,n);
        for(int i=1; i<=m; i++)
        {
            anum=0;
            scanf("%d%d",&l,&r);
            query(1,l,r);
            tmp=getmax();
            printf("%d %d\n",tmp.l,tmp.r);
        }
    }
    return 0;
}