块状链表

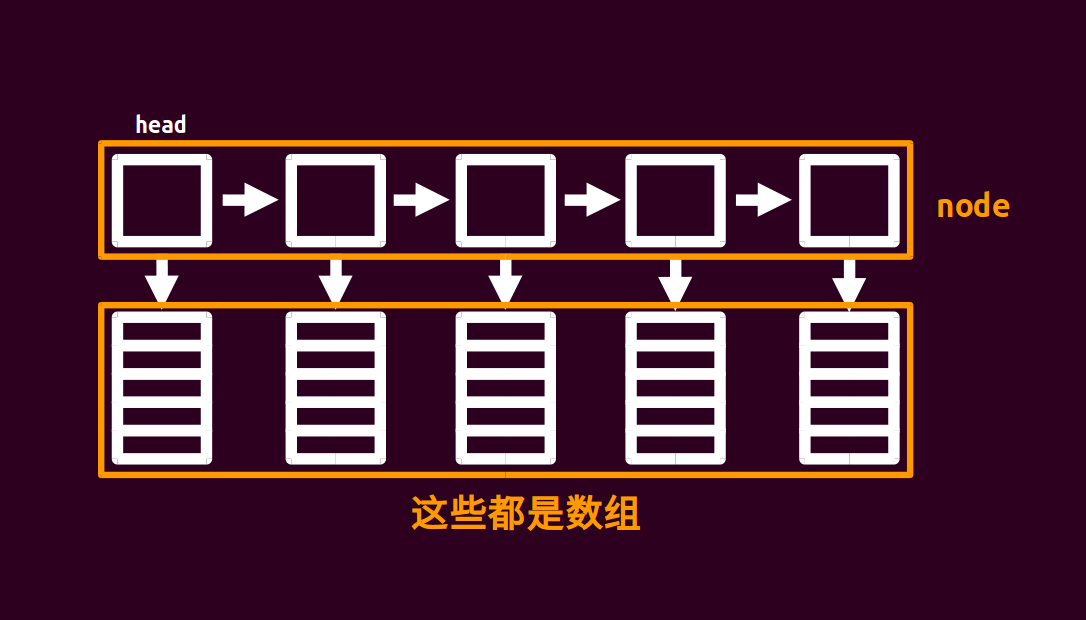
大概就长这样。。。

不难发现块状链表就是一个链表，每个节点指向一个数组。
我们把原来长度为 n 的数组分为√n 个节点，每个节点对应的数组大小为√n。
所以我们这么定义结构体，代码见下。
其中 sqn 表示 sqrt(n) 即√n，pb 表示 push_back，即在这个 node 中加入一个元素。

struct node
{
    node*nxt;int size;char d[(sqn<<1)+5];
    node(){size=0,nxt=NULL,memset(d,0,sizeof(d));}
    void pb(char c){d[size++]=c;}
};

块状链表应该至少支持：分裂、插入、查找。
什么是分裂？分裂就是分裂一个 node，变成两个小的 node，以保证每个 node 的大小都接近√n（否则可能退化成普通数组）。当一个 node 的大小超过 2*√n 时执行分裂操作。

分裂操作怎么做呢？先新建一个节点，再把被分裂的节点的后√n 个值 copy 到新节点，然后把被分裂的节点的后√n 个值删掉 (size–)，最后把新节点插入到被分裂节点的后面即可。

块状链表的所有操作的复杂度都是√n 的。

还有一个要说的。
随着元素的插入（或删除），n 会边，√n 也会变。这样块的大小就会变化，我们难道还要每次维护块的大小？

其实不然，把√n 设置为一个定值即可。比如题目给的范围是 10^6，那么√n 就设置为大小为 10^3 的常量，不用更改它。

另外，你想TLE的话那就用 STL 吧，也没人拦你。
对吧z(j)yf?
这样子：

list<vector<char> > orz_list;

例题

Big String POJ – 2887

题解：
很简单的模板题。代码如下：

#include <cstdio>
#include <cstring>
#include <cctype>
using namespace std;
static const int sqn=1e3;
struct node
{
    node*nxt;int size;char d[(sqn<<1)+5];
    node(){size=0,nxt=NULL;}
    void pb(char c){d[size++]=c;}
}*head=NULL;
char inits[(int)1e6+5];
int llen,q;
void readch(char & ch){do ch=getchar();while(!isalpha(ch));}
void check(node*p)
{
    if(p->size>=(sqn<<1))
    {
        node*q=new node;
        for(int i=sqn;i<p->size;i++)q->pb(p->d[i]);
        p->size=sqn,q->nxt=p->nxt,p->nxt=q;
    }
}
void insert(char c,int pos)
{
    node*p=head;int tot,cnt;
    if(pos>llen++){while(p->nxt!=NULL)p=p->nxt;p->pb(c),check(p);return;}
    for(tot=head->size;p!=NULL&&tot<pos;p=p->nxt,tot+=p->size);
    tot-=p->size,cnt=pos-tot-1;
    for(int i=p->size-1;i>=cnt;i--)p->d[i+1]=p->d[i];
    p->d[cnt]=c,p->size++;
    check(p);
}
char query(int pos)
{
    node*p;int tot,cnt;
    for(p=head,tot=head->size;p!=NULL&&tot<pos;p=p->nxt,tot+=p->size);
    tot-=p->size;return p->d[pos-tot-1];
}
int main()
{
    scanf("%s %d",inits,&q),llen=strlen(inits);
    node*p=new node;head=p;
    for(int i=0;i<llen;i++)
    {
        if(i%sqn==0&&i)p->nxt=new node,p=p->nxt;
        p->pb(inits[i]);
    }
    char a;int k;
    while(q--)
    {
        readch(a);
        if(a=='Q')scanf("%d",&k),printf("%c\n",query(k));
        else readch(a),scanf("%d",&k),insert(a,k);
    }
    return 0;
}