【题解】[Balkan 2011]Timeismoney 凸包+最小生成树+线性变换 BZOJ – 2395

题目戳我

神题一道，网上大部分做法都是叉积然后最大生成树（似乎一开始需要两次最小生成树？），我用的是线性变换最小生成树，本质应该差不多。

首先假设我们能枚举出所有的方案，每个方案用一个二维平面的点 $(\sum c, \sum t)$表示

我们要找的就是 $x \times y$最小的点，也就是在 $k$最小的反比例函数 $xy = k$上的点

这样的点一定在点集的左下凸包上

然后 $x$最小的点和 $y$最小的点都一定在这个凸包上，这个用最小生成树找到就行了

接下来的点用一个叫做 quick hull 的算法找，过程：

现在已知 $x$最小的点和 $y$最小的点，设它们为 $A, B$

作 $A, B$的连线 $AB$

找到 $AB$左下方距离 $AB$最远的点 $C$，这个点 $C$也一定在凸包上

递归处理 $A, C$和 $C, B$

动图出来大概就是（这个是全向凸包，我们只要求左下的就行了）：

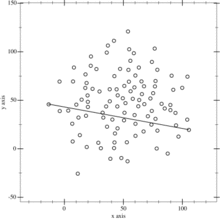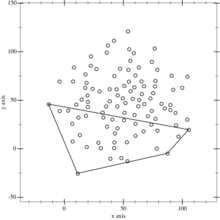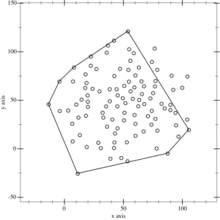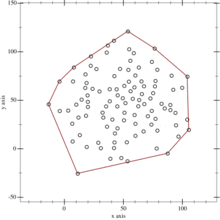
那么问题就是怎么找这个距离 $AB$最远的点 $C$

很多同学的思路是找到叉积最大的点，我第一反应是把空间线性变换，旋转整个空间，使得 $\vec {AB}$与 $y$轴正方向同向（这么说可能不严谨，准确地说是与原空间的 $\hat j$同向），并将旋转后的横坐标基 $\hat i$反向，这样问题就变成了找横坐标最小的点，由于线性变换后向量加法等法则依然有效（这不废话吗），用最小生成树就能做了

由于是格点图，因此凸包最多只有 $\sqrt {255n}$的点（网上那些说 $\log n$级别的是什么鬼），复杂度为 $O(\sqrt n m \log _ 2 m)$

感觉很好理解，然而不是特别好写，我加上注释吧

代码：

#include <bits/stdc++.h>

#define NS (205)
#define MS (10005)

using namespace std;

typedef long long LL;

template<typename _Tp> inline void IN(_Tp &dig)
{
    char c; bool flag = 0; dig = 0;
    while (c = getchar(), !isdigit(c)) if (c == '-') flag = 1;
    while (isdigit(c)) dig = dig * 10 + c - '0', c = getchar();
    if (flag) dig = -dig;
}

LL M[2][2]; // 基底

struct vec
{
    LL x, y;
    vec() { x = y = 0; }
    vec(const LL a, const LL b) { x = a, y = b; }
    bool operator != (const vec oth) const { return x != oth.x || y != oth.y; }
    vec operator - (const vec oth)
    {
        return vec(x - oth.x, y - oth.y);
    }
    void operator += (const vec oth)
    {
        x += oth.x, y += oth.y;
    }
    int crs(const vec oth) { return x * oth.y - y * oth.x; } // 叉乘
    void trans() // 变换
    {
        LL a, b;
        a = x * M[0][0] + y * M[1][0];
        b = x * M[0][1] + y * M[1][1];
        x = a, y = b;
    }
    void untrans() // 逆变换
    {
        LL a, b, c = M[0][0] * M[1][1] - M[0][1] * M[1][0];
        a = (M[1][1] * x - M[1][0] * y) / c;
        b = (M[0][0] * y - M[0][1] * x) / c;
        x = a, y = b;
    }
} ans(1000000, 1000000);

void update(const vec a) // 尝试更新答案
{
    if (a.x * a.y < ans.x * ans.y) ans = a;
    else if (a.x < ans.x && a.x * a.y == ans.x * ans.y) ans = a;
}

int n, m;

struct edge // 边
{
    int a, b;
    vec v;
    bool operator < (const edge oth) const
    {
        return v.x < oth.v.x; // 找横坐标最小的点
    }
} E[MS];

int f[NS]; // 并查集

int findf(int a) { return f[a] == a ? a : f[a] = findf(f[a]); }

vec run(vec bx, vec by) // bx, by 组成一组基底
{
    M[0][0] = bx.x, M[0][1] = bx.y;
    M[1][0] = by.x, M[1][1] = by.y;
    for (int i = 1; i <= n; i += 1) f[i] = i;
    for (int i = 1; i <= m; i += 1) E[i].v.trans(); // 对整个空间进行变换
    sort(E + 1, E + 1 + m); // 最小生成树
    vec res;
    for (int i = 1, j = 1; i <= m && j < n; i += 1)
    {
        int fa = findf(E[i].a), fb = findf(E[i].b);
        if (fa == fb) continue;
        j++, res += E[i].v, f[fa] = fb;
    }
    for (int i = 1; i <= m; i += 1) E[i].v.untrans(); // 逆变换回来，撤销操作
    res.untrans(); // 返回原空间的向量
    return res;
}

void hull(vec s, vec t) // quick hull 找凸包
{
    vec i = t - s, k = run(vec(-i.y, i.x), i), j = k - s;
    if (j.crs(i) <= 0) return; // 已经没有凸出去的点了就返回
    update(k), hull(s, k), hull(k, t);
}

int main(int argc, char const* argv[])
{
    IN(n), IN(m);
    for (int i = 1; i <= m; i += 1)
    {
        IN(E[i].a), IN(E[i].b), IN(E[i].v.x), IN(E[i].v.y);
        E[i].a++, E[i].b++;
    }
    vec s = run(vec(1, 0), vec(0, 1));
    vec t = run(vec(0, -1), vec(1, 0));
    update(s), update(t);
    if (s != t) hull(s, t);
    printf("%lld %lld\n", ans.x, ans.y);
    return 0;
}