题解
一个优化建图的例题
首先题目明示跑网络流,然而操作 $2,3,4$因为涉及到一段连续的点,连边会爆炸,所以我们考虑用线段树优化建图
优化建图实际上就是利用线段树的特性,将连续的一段点变成一个点,这种东西脑补一下就明白了,但是还是画个图吧 $qwq$
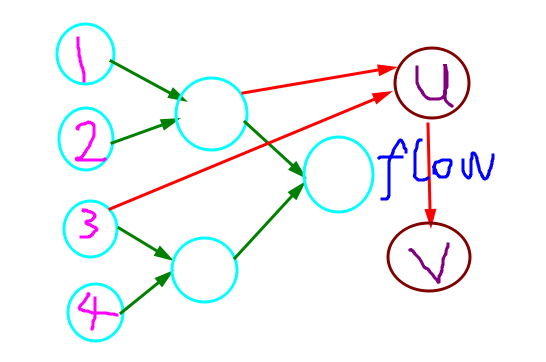
如果你想连 $1-3$号点的话你只需要这样连。并且在 $n$个点的情况下是 $logn$的连边数
然后你就大概可以 $A$了。
分析一下复杂度吧
首先线段树的点数是 $O(2k)$的,然后辅助点最坏情况下是 $O(2m)$,边数是 $mlogk$的,所以空间是不会爆的。就是时间有一点卡
恩大概是天生脸黑吧我就被卡了
然后随便加了个当前弧优化就莽过去了
这告诫我们当前弧优化还是加吧不然容易 $gg$(好像我以前测试过当前弧优化在普通的图里能提高三倍效率,不过这种构造图就不是特别明显毕竟 $s$离 $t$的距离本身就很小,多次 $dfs$的几率会比较小)
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<ctype.h>
#include<queue>
#define Re register
#define fo(i, a, b) for (Re int i = (a); i <= (b); ++i)
#define fd(i, a, b) for (Re int i = (a); i >= (b); --i)
#define edge(i, u) for (Re int i = head[u], v = e[i].v; i; i = e[i].nxt, v = e[i].v)
#define pb push_back
#define F first
#define S second
#define ll long long
#define inf 1000000007
#define mp std::make_pair
#define eps 1e-4
#define mod 998244353
#define lowbit(x) (x & -x)
#define N 2500005
#define clr(arr) memset(arr, 0, sizeof arr)
#define bset std::bitset<N>
inline void read (int &x)
{
x = 0;
Re bool flag = 0;
Re char ch = getchar();
while (!isdigit(ch) && ch != '-') ch = getchar();
if (ch == '-') flag = 1, ch = getchar();
while (isdigit(ch)) x = (x << 3) + (x << 1) + ch - '0', ch = getchar();
if (flag) x = -x;
}
struct edge {
int nxt, v, w;
} e[N << 1];
int n, m, k, tot = 1, head[N], cnt;
using namespace std;
inline void addedge (int u, int v, int w)
{
e[++tot] = (edge) {head[u], v, w};
head[u] = tot;
e[++tot] = (edge) {head[v], u, 0};
head[v] = tot;
}
int s, t, que[N], hh, tt, dis[N], cur[N];
inline bool bfs ()
{
memset(dis, 0, sizeof dis);
dis[s] = 1;
que[hh = tt = 1] = s;
while (hh <= tt)
{
int u = que[hh++];
edge (i, u)
if (e[i].w && !dis[v])
{
que[++tt] = v;
dis[v] = dis[u] + 1;
}
}
return dis[t];
}
inline int dfs (int u, int cap)
{
if (u == t) return cap;
Re int used = 0;
for (Re int i = cur[u], v = e[i].v; i; i = e[i].nxt, v = e[i].v)
if (e[i].w && dis[v] == dis[u] + 1)
{
Re int now = dfs(v, min(cap - used, e[i].w));
if (now)
{
used += now;
e[i].w -= now;
e[i ^ 1].w += now;
if (used == cap) { cur[u] = i; return cap; }
}
}
return used;
}
inline int dinic ()
{
int ret = 0, now;
while (bfs())
{
memcpy(cur, head, sizeof cur);
while (now = dfs(s, inf)) ret += now;
}
return ret;
}
int id[N], l;
int opt, u1, u2, v1, v2, fr, to;
struct segment_tree {
int opt, pos[N];
#define ls (u << 1)
#define rs (u << 1 | 1)
inline void build (int u, int L, int R)
{
if (L == R)
{
pos[u] = id[L];
return;
}
pos[u] = ++cnt;
int mid = L + R >> 1;
build(ls, L, mid); build(rs, mid + 1, R);
if (!opt) addedge(pos[u], pos[ls], inf), addedge(pos[u], pos[rs], inf);
else addedge(pos[ls], pos[u], inf), addedge(pos[rs], pos[u], inf);
}
inline void modify (int u, int L, int R, int l, int r)
{
if (l <= L && R <= r)
{
if (opt) addedge(pos[u], fr, inf);
else addedge(to, pos[u], inf);
return;
}
int mid = L + R >> 1;
if (l <= mid) modify(ls, L, mid, l, r);
if (mid < r) modify(rs, mid + 1, R, l, r);
}
} t1, t2;
int main ()
{
scanf("%d %d %d", &n, &m, &k);
cnt = 2;
s = 1; t = 2;
fo (i, 1, k) id[i] = ++cnt;
addedge(s, id[1], n);
addedge(id[k], t, n);
t1.opt = 1;
t1.build(1, 1, k); t2.build(1, 1, k);
while (m--)
{
read(opt); read(l);
if (opt == 1)
{
read(u1); read(v1);
addedge(id[u1], id[v1], l);
}
else
if (opt == 2)
{
read(u1); read(u2); read(v1);
fr = ++cnt; to = id[v1];
t1.modify(1, 1, k, u1, u2);
addedge(fr, to, l);
}
else
if (opt == 3)
{
read(u1); read(v1); read(v2);
fr = id[u1]; to = ++cnt;
t2.modify(1, 1, k, v1, v2);
addedge(fr, to, l);
}
else
if (opt == 4)
{
read(u1); read(u2); read(v1); read(v2);
fr = ++cnt, to = ++cnt;
t1.modify(1, 1, k, u1, u2);
t2.modify(1, 1, k, v1, v2);
addedge(fr, to, l);
}
}
printf("%d", dinic());
return 0;
}
0 条评论