题目分析

一条边将多边形分成了 “面对 $n$点” 的一侧和 “背对 $n$点” 的一侧。“背对 $n$点的一侧” 构成了一个点区间，这就是这条边管理的区间。因为不存在相交的边，所以每条边管理的区间之间存在嵌套关系，可以写成树结构。又发现因为整个多边形被严格分成了 $n-3$个三角形，所以形成的东西是二叉树森林，其中每棵树的根代表转一下就会和 $n$相连的边。

最终状态一定是所有划分边（即不是构成多边形的边）都和 $n$相连。

最优方案一定是依次将所有划分边都转成和 n 相连的，并且若还存在不与 $n$相连的划分边，一定可以完成一次将一条边转成和 n 相连的操作，所以最少操作次数是 $n-3-$与 $n$相连的划分边数。

将二叉树森林画出来后，发现一定要转完一个点的所有祖先，转它的时候才能正好把它转成和 $n$相连的。

于是计算方案数也很好办了，若当前节点左子树要转 $a$次，右子树要转 $b$次，则方案数要乘以 $C _ {a+b} ^ a$。还要用组合数算一下不同的二叉树之间旋转方式排列好的方案数。

对于多组询问，发现若你要转一条边，它代表的点一定是其父亲的左儿子。若父亲管理的区间是
$(l,r)$，它管理的区间是 $(l,k)$，它的左儿子管理的区间是 $(l,k’)$（若无左儿子，$k’=k-1$）。那么转一下它后，它管理的区间将变成 $(k’,r)$。于是需要重排一下几个点的位置，得到新的树（如图）：

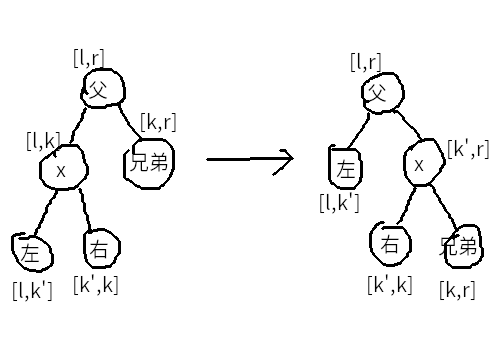
特别像一个 splay 的 zig 对吧？

然后还有若要转的边是某棵二叉树的根节点，贡献的计算方式要特别处理一下（详见代码）。

代码

#include<bits/stdc++.h>
using namespace std;
#define RI register int
int read() {
    int q=0;char ch=' ';
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9') q=q*10+ch-'0',ch=getchar();
    return q;
}
typedef pair<int,int> PR;
const int N=200005,mod=1e9+7;
int typ,n,Q,ans1,ans2,SZ,sum;
int inv[N],fac[N],ifac[N],s[N][2],sz[N],fa[N],rt[N];
vector<int> e[N];
map<PR,int> mp;

int C(int d,int u) {return 1LL*fac[d]*ifac[u]%mod*ifac[d-u]%mod;}
int ksm(int x,int y) {
    int re=1;
    for(;y;y>>=1,x=1LL*x*x%mod) if(y&1) re=1LL*re*x%mod;
    return re;
}
void init() {
    inv[0]=inv[1]=ifac[0]=fac[0]=1;
    for(RI i=1;i<=n+n;++i) fac[i]=1LL*fac[i-1]*i%mod;
    for(RI i=2;i<=n+n;++i) inv[i]=1LL*(mod-mod/i)*inv[mod%i]%mod;
    for(RI i=1;i<=n+n;++i) ifac[i]=1LL*ifac[i-1]*inv[i]%mod;
}
void prework() {
    int x,y;
    for(RI i=1;i<=n-3;++i)
        x=read(),y=read(),e[x].push_back(y),e[y].push_back(x);
    for(RI i=1;i<n;++i) e[i].push_back(i+1),e[i+1].push_back(i);
    e[1].push_back(n),e[n].push_back(1);
    for(RI i=1;i<=n;++i) sort(e[i].begin(),e[i].end());
}
void orzyyb(int &x,int las,int l,int r) {
    if(r-l<=1) return;
    int k=upper_bound(e[r].begin(),e[r].end(),l)-e[r].begin();
    k=e[r][k],x=++SZ,fa[x]=las,mp[(PR){l,r}]=x;
    orzyyb(s[x][0],x,l,k),orzyyb(s[x][1],x,k,r);
    sz[x]=sz[s[x][0]]+sz[s[x][1]]+1;
    ans2=1LL*ans2*C(sz[x]-1,sz[s[x][0]])%mod;
}

int main()
{
    typ=read(),n=read();
    init(),prework();
    ans1=n-1-(int)e[n].size(),ans2=1;
    for(RI i=1;i<(int)e[n].size();++i) {
        orzyyb(rt[i],0,e[n][i-1],e[n][i]);
        sum+=sz[rt[i]],ans2=1LL*ans2*C(sum,sz[rt[i]])%mod;
    }
    if(!typ) printf("%d\n",ans1);
    else printf("%d %d\n",ans1,ans2);
    Q=read();
    while(Q--) {
        int x=read(),y=read(); if(x>y) swap(x,y);
        int k=mp[(PR){x,y}];
        int kans1=ans1-(fa[k]?0:1)+(y==1),kans2=ans2;
        if(fa[k]) {
            int f=fa[k];
            kans2=1LL*kans2*ksm(C(sz[k]-1,sz[s[k][0]]),mod-2)%mod;
            kans2=1LL*kans2*ksm(C(sz[f]-1,sz[s[f][0]]),mod-2)%mod;
            kans2=1LL*kans2*C(sz[s[k][1]]+sz[s[f][1]],sz[s[k][1]])%mod;
            kans2=1LL*kans2*C(sz[f]-1,sz[s[k][0]])%mod;
        }
        else {
            kans2=1LL*kans2*ksm(C(sz[k]-1,sz[s[k][0]]),mod-2)%mod;
            kans2=1LL*kans2*ksm(C(sum,sz[k]),mod-2)%mod;
            kans2=1LL*kans2*C(sum-sz[k]+sz[s[k][0]],sz[s[k][0]])%mod;
            kans2=1LL*kans2*C(sum-sz[k]+sz[s[k][0]]+sz[s[k][1]],sz[s[k][1]])%mod;
        }
        if(!typ) printf("%d\n",kans1);
        else printf("%d %d\n",kans1,kans2);
    }
    return 0;
}