序列自动机好简单啊
首先我们有一个字符串 $S$,记 $nxt[i][j]$表示 $S$的第 $i$位之后第一个字符 $j$的位置。
然后介绍构造算法,其实。。。按照定义来说,这样写就行了
inline void build ()
{
fd (i, n, 1)
{
memcpy(nxt[i - 1], nxt[i], sizeof nxt[i]);
nxt[i - 1][s[i] - 'A'] = i;
}
}
为了能让你感性理解它,我会画一张 $ABA$的图
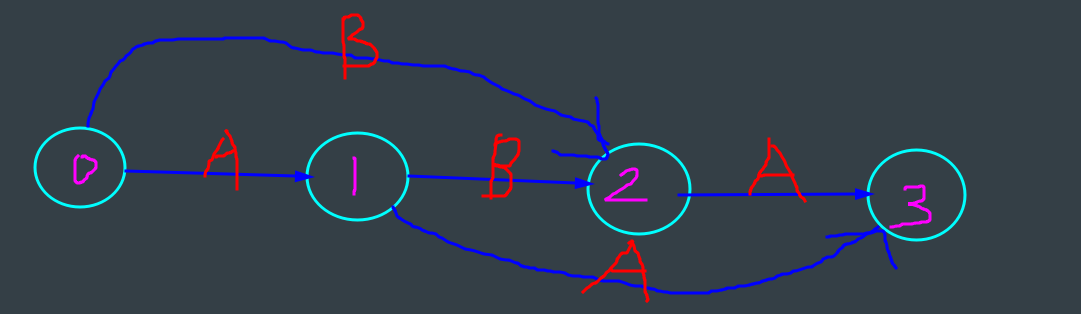
容易知道它的空间复杂度是 $O(n\alpha)$,其中 $\alpha$为字符集大小
然后我们来介绍它的一些性质
1. 任意一条在序列自动机上的路径都是原字符串的一个子序列
性质 $1$显然
2. 从根节点 $0$开始的任意一条路径所代表的子序列都是互不相同的。
性质 $2$显然,如果相同显然会跑到同一个点去
并且由性质 2,我们可以按拓扑逆序 $dp$或者 $dfs$来算出本质不同的子序列个数,方法和后缀自动机差不多。
然后似乎知道这些你就可以做这题了。
首先需要圈出来的是它的字符集竟然是大写和小写字母然后我刚开始就被坑到自闭
对于两个字符串建立序列自动机,然后从根节点开始同时 $dfs$,有相同的扩展边一起扩展就行,然后顺便算出本质不同的子序列个数。
注意这道题的一个坑点,因为当两个字符串很长的时候答案可能会很大,这个时候它也不会让你输出子序列集,而如果要输出子序列集的话就不能记忆化而要全部 $dfs$一遍,否则记忆化乐滋滋,所以这两个东西还是分开写 $dfs$吧。
还有我并不太会算这道题的答案上界。。。似乎上界是一个爆内存的数。。。压位高精都不行的那种。。。至少我手玩了一个 $1000$位的两个大致相同的字符串答案已经到达了 $233$位。。。
所以你问我怎么开高精内存,我也无能为力 $emmmm$
但是据说能存 $180$位就行了 (因为第一个题解就存了这么多)
如果你感兴趣的话你可以试一试我手玩的这组大数据?
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<ctype.h>
#include<queue>
#include<map>
#define Re register
#define fo(i, a, b) for (Re int i = (a); i <= (b); ++i)
#define fd(i, a, b) for (Re int i = (a); i >= (b); --i)
#define edge(i, u) for (Re int i = head[u], v = e[i].v; i; i = e[i].nxt, v = e[i].v)
#define pb push_back
#define F first
#define S second
#define ll long long
#define inf 1000000007
#define mp std::make_pair
#define eps 1e-4
#define mod 10000000
#define lowbit(x) (x & -x)
#define N 3105
#define clr(arr) memset(arr, 0, sizeof arr)
#define bset std::bitset<N>
inline int read ()
{
Re int x = 0; Re bool flag = 0; Re char ch = getchar();
while (!isdigit(ch) && ch != '-') ch = getchar();
if (ch == '-') flag = 1, ch = getchar();
while (isdigit(ch)) x = (x << 3) + (x << 1) + (ch ^ 48), ch = getchar();
if (flag) x = -x; return x;
}
struct sqam {
int nxt[N][58], n;
char s[N];
inline void build ()
{
fd (i, n, 1)
{
memcpy(nxt[i - 1], nxt[i], sizeof nxt[i]);
nxt[i - 1][s[i] - 'A'] = i;
}
}
}s1, s2;
struct big {
int n, f[50];
inline void init ()
{
memset(f, 0, sizeof f);
n = 0;
}
inline void add (big x)
{
int up = std::max(n, x.n);
fo (i, 1, up)
f[i] += x.f[i];
fo (i, 1, up)
if (f[i] >= mod)
{
f[i] -= mod;
f[i + 1]++;
}
if (f[up + 1]) ++up;
n = up;
}
inline void print ()
{
printf("%d", f[n]);
fd (i, n - 1, 1) printf("%07d", f[i]);
}
};
int opt, top;
big dp[N][N], one;
char s[N];
inline void dfs1 (int x, int y)
{
if (dp[x][y].n) return;
dp[x][y].init();
dp[x][y].add(one);
fo (i, 0, 57)
if (s1.nxt[x][i] && s2.nxt[y][i])
{
dfs1(s1.nxt[x][i], s2.nxt[y][i]);
dp[x][y].add(dp[s1.nxt[x][i]][s2.nxt[y][i]]);
}
}
inline void dfs (int x, int y)
{
printf("%s\n", s + 1);
fo (i, 0, 57)
if (s1.nxt[x][i] && s2.nxt[y][i])
{
s[++top] = i + 'A';
dfs(s1.nxt[x][i], s2.nxt[y][i]);
s[top--] = ' ';
}
}
int main ()
{
one.init(); one.n = 1; one.f[1] = 1;
s1.n = read(); s2.n = read();
scanf("%s", s1.s + 1);
scanf("%s", s2.s + 1);
s1.build(); s2.build();
opt = read();
dfs1(0, 0);
if (opt) dfs(0, 0);
dp[0][0].print();
return 0;
}
0 条评论