【题解】[HNOI2017] 队长快跑 单调队列+计算几何 loj2022 —Qiuly

题目传送门

洛谷数据的锅终于修好了（于是我成为了修好数据后 $\rm{A}$ 掉的第一人（QAQ

$\text{sto Freopen} $ 。

这个火焰喜欢乱射，很烦，不过稍微仔细一点可以发现，每次绕过一个火焰，要么是从其下面绕过，要么是从其上面绕过，所以可以分成两类，一类是朝上的，一类是朝下的。

接下来就是找最优答案。

考虑维护两个队列，分别维护朝上的和朝下的火焰，接下来将所有火焰按照 $x$ 从小到大加入队列。

假设当前需要加入的火焰是朝上的，并且当前情况如下：

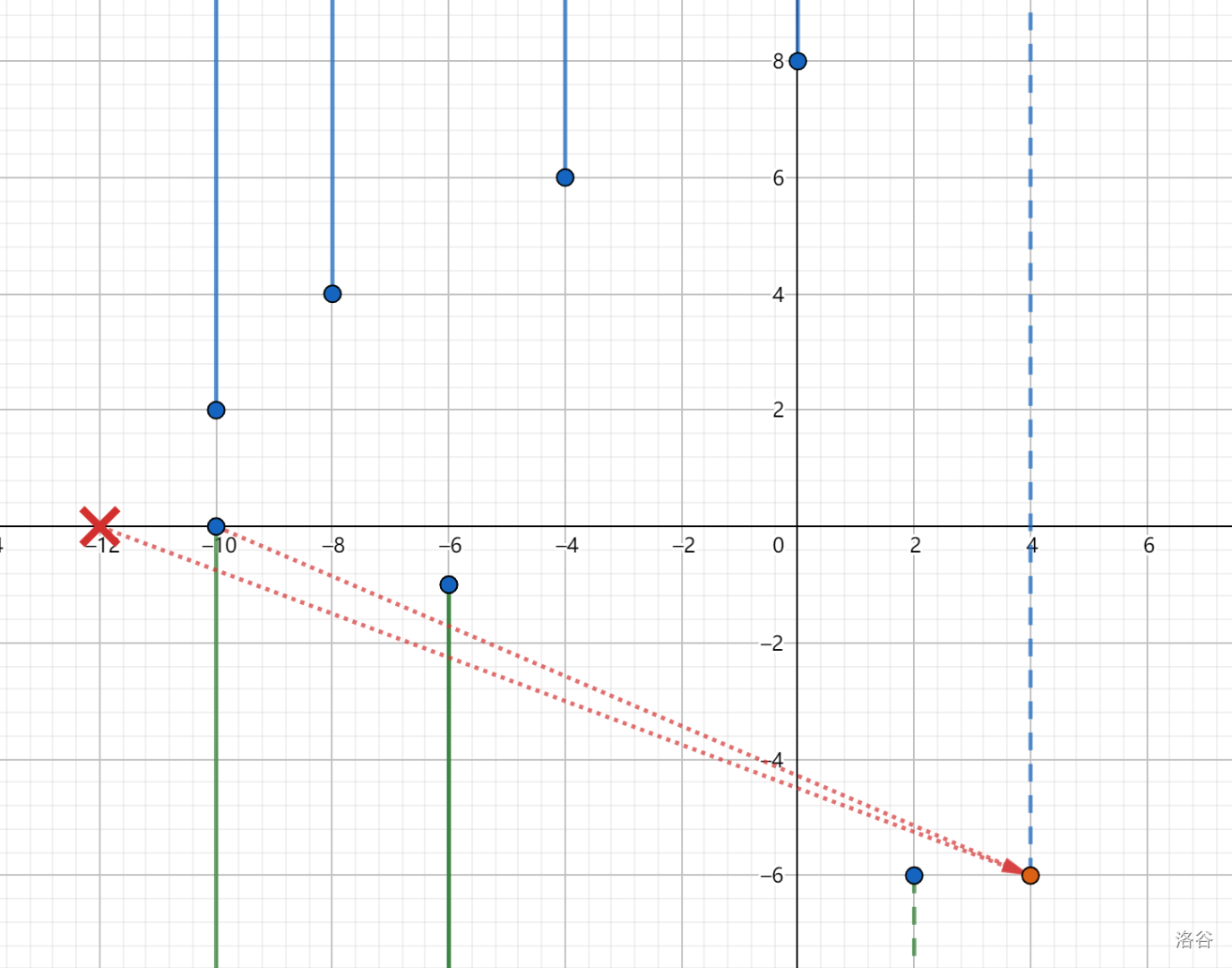
当前加入火焰 (橙色点，简称为 $a$ 点)，与起点 (红叉，简称 $S$ 点) 的最短路被第一个向下的火焰 $t_1$ 和第二个向下的火焰 $t_2$ 截断了。

首先 $t_2$ 到 $S$ 的路径被 $t_1$ 截断了，那么从队列里面删除 $S$ ，因为后面再加入什么火焰往前走的最优路径在一定要到 $t_1$ 才能到 $S$ ，可以画图想想为什么。

所以对于这种情况 (也就是当前加入的火焰与 $S$ 的最优路径被另一朝向的火焰截断了)，直接从队尾一个一个弹出这样的 $S$ 即可。

然后是另一种情况，两边相安无事：

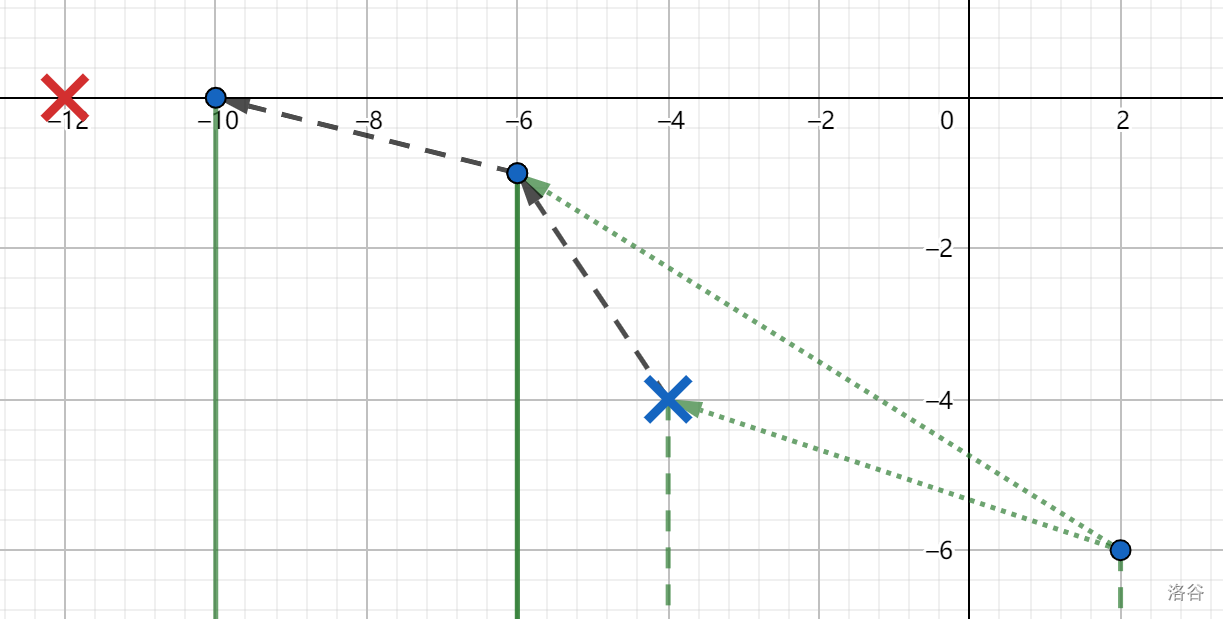
加入了 $a$ 后，容易发现蓝叉 ($t_3$) 一定是没用了的，首先 $a$ 到 $t_2$ 走两点间的最短距离更优。

很显然，如果后来一个火焰 $b$ 的 $y$ 小于 $a$ 的 $y$ ，那么如果去到 $t_3$ 再去之前的，肯定不比去到 $a$ 然后去之前的更优。

如果 $b$ 的 $y$ 大于 $a$ 的 $y$ ，那么为什么不直接跳到之前的呢？

所以对于这种情况，直接从队尾一个一个弹出这样的 $t_3$ 即可。

#include <cmath>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;

const int N=1e6+2;
int q[2][N],head[2],tail[2];
int n,m,ID[N],pre[N],tmp[N],dir[N];
struct Node {
    ll x,y;
    Node(ll _x=0,ll _y=0):x(_x),y(_y){}
    Node operator - (const Node&b) const {return (Node){x-b.x,y-b.y};}
    ll operator * (const Node&b) const {return x*b.y-y*b.x;}
}S,T,A[N],P[N];

bool cmp(int x,int y) {return A[x].x<A[y].x;}
inline bool cross(int x,int y,int z,int flag) {
    return (bool)((P[x]-P[y])*(P[z]-P[y])*flag>=0);
}
int main() {
    scanf("%d%lld%lld",&n,&T.x,&T.y);
    for(int i=1;i<=n;++i) {
        double l,r,t;
        scanf("%lld%lld%lf",&A[i].x,&A[i].y,&t);
        l=atan2(S.y-A[i].y,S.x-A[i].x),
        r=atan2(T.y-A[i].y,T.x-A[i].x);
        tmp[i]=(l<r)?(l<t&&t<r):(!(r<t&&t<l)),ID[i]=i;
    }
    sort(ID+1,ID+1+n,cmp),
    P[++m]=S;
    for(int i=1;i<=n&&A[ID[i]].x<T.x;++i)
        if(A[ID[i]].x>S.x) P[++m]=A[ID[i]],dir[m]=tmp[ID[i]];
    P[++m]=T;
    q[0][1]=q[1][1]=1;
    for(int i=1;i<=m;++i) {
        int dir=::dir[i],res=dir?-1:1;
        int &l0=head[dir],&r0=tail[dir],*q0=q[dir];
        int &l1=head[dir^1],&r1=tail[dir^1],*q1=q[dir^1];
        if(l1<r1&&cross(i,q1[l1],q1[l1+1],res)) {
            while(l1<r1&&cross(i,q1[l1],q1[l1+1],res)) ++l1;
            pre[i]=q0[l0=r0=r0+1]=q1[l1];
        } else {
            while(l0<r0&&cross(i,q0[r0-1],q0[r0],res)) --r0;
            pre[i]=q0[r0];
        }
        q0[++r0]=i;
    }
    double ans=0.0;
    for(int i=m;i>1;i=pre[i]) {
        double _1=P[i].x-P[pre[i]].x;
        double _2=P[i].y-P[pre[i]].y;
        ans+=sqrt(_1*_1+_2*_2);
    }
    printf("%.10lf\n",ans);
    return 0;
}