首先对于需要按奇数次的开关,其生成函数为:
$$
F_i(x)=\sum_{n\,is\,odd}^{\infty}p_i^{n}\frac{x^{n}}{n!}
$$
然后对于需要按偶数次的开关,其生成函数为:
$$
F_i(x)=\sum_{n\,is\,even}^{\infty}p_i^{n}\frac{x^{n}}{n!}
$$
补充一下 $\rm{EGF}$ 的一些常用公式,首先最基础的:
$$
e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}=1+\frac{x^1}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots+\frac{x^n}{n!}+\cdots\\
e^{-x}=\sum_{n=0}^{\infty}(-1)^{n}\frac{x^n}{n!}=1-\frac{x^1}{1!}+\frac{x^2}{2!}-\frac{x^3}{3!}+\cdots+(-1)^n\frac{x^n}{n!}+\cdots\\
$$
根据上面两个公式可以得到:
$$
\sum_{n\,is\,odd}^{\infty}\frac{x^n}{n!}=\frac{x^1}{1!}+\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots+[n\text{ is odd}]\frac{x^n}{n!}+\cdots=\frac{e^x-e^{-x}}{2}\\
\sum_{n\,is\,even}^{\infty}\frac{x^n}{n!}=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\frac{x^6}{6!}+[n\text{ is even}]\frac{x^n}{n!}+\cdots=\frac{e^x+e^{-x}}{2}\\
$$
上面的两个就可以简化了:
$$
F_i(x)=
\begin{cases}
\frac{e^{p_ix}-e^{-p_ix}}{2}\quad\text{if }i\text{ is odd}\\
\frac{e^{p_ix}+e^{-p_ix}}{2}\quad\text{if }i\text{ is even}\\
\end{cases}
$$
也可以写成:
$$
F_i(x)=\frac{e^{p_ix}+(-1)^{s_i}e^{-p_ix}}{2}
$$
然后令:
$$
\begin{aligned}
F(x)&=\prod_{i=1}^{n}F_i(x)\\
&=\prod_{i=1}^{n}\frac{e^{p_ix}+(-1)^{s_i}e^{-p_ix}}{2}\\
\end{aligned}
$$
假设遇到合法状态后还会继续按,对于按 $k$ 次开关才可以通过的概率为 $F(x)$ 的 $x^k$ 的系数。
令 $C(x)$ 的 $x^k$ 的系数表示按了 $k$ 次后,第一次出现合法状态的概率,令 $G(x)$ 的 $x^k$ 的系数表示一个状态再操作 $k$ 次后依旧是这个状态的概率。
根据 $G(x)$ 的定义,可以很简单的写出来 $G(x)$ 的式子:
$$
G(x)=\prod_{i=1}^{n}\frac{e^{p_ix}+e^{-p_ix}}{2}\\
$$
然后显然有 $C(x)G(x)=F(x)$,也就是 $C(x)=\frac{F(x)}{G(x)}$ 。
想一想答案是什么,对于权值为 $k$ ,其概率为 $C(x)$ 的 $x^k$ 的系数。
在这里令 $ans_k$ 表示 $C(x)$ 的 $x^k$ 的系数,那么答案为:
$$
ans=\sum_{i=0}^{\infty}i\cdot ans_i
$$
对于这个 $i$ ,对 $C(x)$ 求个导。求导的话,首先原来的 $x^0$ 会消失,但是本来我们就不关心 $x^0$ 的系数,因为权值是 $0$ ,对答案的贡献也就是 $0$ 。
至于求导后 $x^n$ 会变成 $nx^{n-1}$ 的话,因为这时我们并不关心某一项的系数,只关心总和,所以对于表示项数的 $x$ 直接忽略不管即可。
令 $x=1$ ,答案就是 $C'(1)$ 了:
$$
\begin{aligned}
C'(1)=\left(\frac{F(1)}{G(1)}\right)’
\end{aligned}
$$
补充一下怎么求一个函数除一个函数的导数,可以参考一下 维基百科
$$
\left(\frac{f(x)}{g(x)}\right)’=\frac{f'(x)g(x)-g'(x)f(x)}{[g(x)]^2}
$$
结论如上,证明如下:令 $h(x)=\frac{f(x)}{g(x)}$ ,有 $f(x)=g(x)h(x)$ :
$$
f'(x)=g'(x)h(x)+g(x)h'(x)\\
$$
移项后:
$$
\begin{aligned}
h'(x)&=\frac{f'(x)-g'(x)h(x)}{g(x)}\\
&=\frac{f'(x)-g'(x)\frac{f(x)}{g(x)}}{g(x)}\\
&=\frac{f'(x)g(x)-g'(x)f(x)}{[g(x)]^2}\\
\end{aligned}
$$
于是现在我们就需要求这个玩意:
$$
\frac{F'(1)G(1)-G'(1)F(1)}{[G(1)]^2}
$$
回忆一下 $F,G$ :
$$
\begin{aligned}
F(x)&=\prod_{i=1}^{n}\frac{e^{p_ix}+(-1)^{s_i}e^{-p_ix}}{2}\\
G(x)&=\prod_{i=1}^{n}\frac{e^{p_ix}+e^{-p_ix}}{2}\\
\end{aligned}
$$
将 $x=1$ 带入:
$$
\begin{aligned}
F(1)&=\prod_{i=1}^{n}\frac{e^{p_i}+(-1)^{s_i}e^{-p_i}}{2}\\
G(1)&=\prod_{i=1}^{n}\frac{e^{p_i}+e^{-p_i}}{2}\\
\end{aligned}
$$
现在求的是 $\sum\limits_{i=0}^{\infty}p_i\frac{x^i}{i!}$ ,但是最终我们要求的是 $\sum\limits_{i=0}^{\infty}p_ix^i$ ,于是将 $F,G$ 转换为 $\rm{OGF}$ ,以 $F$ 为例。
对于 $e^{p_i}+(-1)^{s_i}e^{-p_i}$ 这个式子,显然可以表示为下述形式:
$$
\sum_{i=-\infty}^{\infty}a_ie^{ix}
$$
这个 $a_i$ 表示系数,除了 $i=p_i$ 和 $i=-p_i$ 两个地方,其他的 $a_i$ 都为 $0$ 。
然后现在将 $e^{p_i}+(-1)^{s_i}e^{-p_i}$ 和 $e^{p_j}+(-1)^{s_j}e^{-p_j}$ 相乘,容易发现乘出来的结果也符合上述形式。所以 $F,G$ 也可以表示为上述形式。
对于 $e^{cx}$ ,转成 $\rm{OGF}$ 也就是 $\frac{1}{1-cx}$ ,也就是这个形式:
$$
\sum_{i=-\infty}^{\infty}\frac{a_i}{1-ix}
$$
注意一下这里 $i$ 不是整数,并且可以被表示为 $\frac{k}{P}$ 的形式,其中 $P$ 是 $\sum p_i$ ,$k$ 是整数。
那么就有:
$$
\begin{aligned}
F(x)&=\sum_{i=-P}^{P}\frac{a_i}{1-\frac{i}{P}x}\\
G(x)&=\sum_{i=-P}^{P}\frac{b_i}{1-\frac{i}{P}x}\\
\frac{F(x)}{G(x)}&=\frac{\sum\limits_{i=-P}^{P}\frac{a_i}{1-\frac{i}{P}x}}{\sum\limits_{i=-P}^{P}\frac{b_i}{1-\frac{i}{P}x}}=\frac{\sum\limits_{i=-P}^{P}a_{\frac{i}{P}}\prod\limits_{j=-P,j\not=i}^{P}(1-\frac{j}{P}x)}{\sum\limits_{i=-P}^{P}b_{\frac{i}{P}}\prod\limits_{j=-P,j\not=i}^{P}(1-\frac{j}{P}x)}\\
\end{aligned}
$$
考虑令:
$$
A(x)=\sum\limits_{i=-P}^{P}a_{\frac{i}{P}}\prod\limits_{j=-P,j\not=i}^{P}(1-\frac{j}{P}x)\\
B(x)=\sum\limits_{i=-P}^{P}b_{\frac{i}{P}}\prod\limits_{j=-P,j\not=i}^{P}(1-\frac{j}{P}x)\\
$$
观察我们要求的东西:
$$
\frac{F'(1)G(1)-G'(1)F(1)}{[G(1)]^2}
$$
上下同时除一个数,答案是不会变的,所以答案其实是:
$$
\frac{A'(1)B(1)-A'(1)B(1)}{[B(1)]^2}
$$
最后一个问题,怎么求 $A'(x)$ 和 $B'(x)$ ?
补充一下怎么求一个函数乘一个函数的导数。
$$
(F(x)G(x))’=F'(x)G(x)+F(x)G'(x)
$$
扩展一下:
$$
\left(\prod_{i=1}^{n}F_i(x)\right)’=\prod_{i=1}^{n}F_i’(x)\left(\prod_{j=1,j\not=i}^{n}F_j(x)\right)
$$
为了方便,$i$ 将写成分数形式。( $P$ 的定义在上文已经给出) 。
那么可以得到:
$$
\begin{aligned}
A’(x)&=\left(\sum\limits_{i=-P}^{P}a_{\frac{i}{P}}\prod\limits_{j=-P,j\not=i}^{P}(1-\frac{j}{P}x)\right)’\\
&=\sum\limits_{i=-P}^{P}\left(a_{\frac{i}{P}}\prod\limits_{j=-P,j\not=i}^{P}(1-\frac{j}{P}x)\right)’\\
&=\sum\limits_{i=-P}^{P}a_{\frac{i}{P}}\left(\prod\limits_{j=-P,j\not=i}^{P}(1-\frac{j}{P}x)\right)’\\
&=\sum\limits_{i=-P}^{P}a_{\frac{i}{P}}\left(\prod\limits_{j=-P,j\not=i}^{P}(1-\frac{j}{P}x)’\left(\prod\limits_{k=-P,k\not=j,k\not=i}^{P}(1-\frac{k}{P}x)\right)\right)\\
&=\sum\limits_{i=-P}^{P}a_{\frac{i}{P}}\left(\prod\limits_{j=-P,j\not=i}^{P}(-\frac{j}{P})\left(\prod\limits_{k=-P,k\not=j,k\not=i}^{P}(1-\frac{k}{P}x)\right)\right)\\
\end{aligned}
$$
现在,带入 $x=1$ 。
至于为什么之前不能直接带入 $x=1$ ,是因为 $(A(1))’$ 不等价于 $A'(1)$ 。
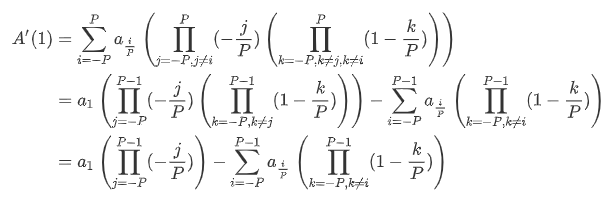
(公式挂了插个图算了 /kel)
考虑令:
$$
S=\prod\limits_{k=-P}^{P-1}(1-\frac{k}{P})
$$
可以得到:
$$
A'(1)=a_1\left(\prod\limits_{j=-P}^{P-1}(-\frac{j}{P})\frac{S}{1-\frac{j}{P}}\right)-\sum_{i=-P}^{P-1}a_{\frac{i}{P}}\frac{S}{1-\frac{i}{P}}\\
$$
$B'(1)$ 的推导一模一样,现在计算 $A'(1)$ 和 $B'(1)$ 的时间复杂度是 $O(P)$ 的了 (可能带个逆元的 $\log$) 。
最后:
$$
A(1)=a_{1}\prod\limits_{j=-P}^{P-1}(1-\frac{j}{P})\\
B(1)=b_{1}\prod\limits_{j=-P}^{P-1}(1-\frac{j}{P})\\
A'(1)=a_1\left(\prod\limits_{j=-P}^{P-1}(-\frac{j}{P})\frac{S}{1-\frac{j}{P}}\right)-\sum_{i=-P}^{P-1}a_{\frac{i}{P}}\frac{S}{1-\frac{i}{P}}\\
B'(1)=b_1\left(\prod\limits_{j=-P}^{P-1}(-\frac{j}{P})\frac{S}{1-\frac{j}{P}}\right)-\sum_{i=-P}^{P-1}b_{\frac{i}{P}}\frac{S}{1-\frac{i}{P}}\\
$$
爆算这四个的时间复杂度是 $O(P)$ 的。
对于 $a,b$ ,直接背包爆算,时间复杂度是 $O(nP)$ 的。
Code:
int main() {
#ifndef ONLINE_JUDGE
freopen(".in","r",stdin);
// freopen(".out","w",stdout);
#endif
IN(n);
for(int i=1;i<=n;++i) IN(s[i]);
for(int i=1;i<=n;++i) IN(p[i]),P+=p[i];
invP=modpow(P,mod-2);
memset(tmp,0,sizeof(tmp)),tmp[0][P]=1;
for(int i=1;i<=n;++i) {
int tag=(s[i]&1)?mod-1:1;
for(int j=0;j<=P+P;++j) if(tmp[i-1][j]) {
if(j+p[i]>=0&&j+p[i]<=P+P) pls(tmp[i][j+p[i]],tmp[i-1][j]);
if(j-p[i]>=0&&j-p[i]<=P+P) pls(tmp[i][j-p[i]],mul(tag,tmp[i-1][j]));
}
}
for(int i=0;i<=P+P;++i) a[i]=tmp[n][i];
memset(tmp,0,sizeof(tmp)),tmp[0][P]=1;
for(int i=1;i<=n;++i)
for(int j=0;j<=P+P;++j) if(tmp[i-1][j]) {
if(j+p[i]>=0&&j+p[i]<=P+P) pls(tmp[i][j+p[i]],tmp[i-1][j]);
if(j-p[i]>=0&&j-p[i]<=P+P) pls(tmp[i][j-p[i]],tmp[i-1][j]);
}
for(int i=0;i<=P+P;++i) b[i]=tmp[n][i];
int A=a[P+P],B=b[P+P],T1=1,T2=1,S=1;
for(int i=0;i<P+P;++i) A=mul(A,dec(1,mul(dec(i,P),invP)));
for(int i=0;i<P+P;++i) B=mul(B,dec(1,mul(dec(i,P),invP)));
for(int i=0;i<P+P;++i) S=mul(S,dec(1,mul(dec(i,P),invP)));
for(int i=0;i<P+P;++i) T1=mul(T1,mod-mul(dec(i,P),invP));
for(int i=0;i<P+P;++i) T2=mul(T2,mul(S,modpow(dec(1,mul(dec(i,P),invP)),mod-2)));
int _A=mul(a[P+P],mul(T1,T2)),_B=mul(b[P+P],mul(T1,T2));
for(int i=0;i<P+P;++i) sub(_A,mul(a[i],mul(S,modpow(dec(1,mul(dec(i,P),invP)),mod-2))));
for(int i=0;i<P+P;++i) sub(_B,mul(b[i],mul(S,modpow(dec(1,mul(dec(i,P),invP)),mod-2))));
int ans=mul(dec(mul(_A,B),mul(A,_B)),modpow(mul(B,B),mod-2));
printf("%d\n",ans);
return 0;
}
0 条评论