题面
题意
给定一个字符串 $s$ (起始位置为 $1$), 对 $s$ 的每个前缀求出最小循环表示的起始位置.
输入样例
abaacaba
输出样例
1 1 3 3 3 6 3 8
数据范围
$|s| \le 3 \times 10^6$.
思路
假设先从前往后扫一遍, 则对于每个前缀, 它的某些后缀可以作为最优答案 (我们称它为有效的), 有些后缀可以被排除.
并且我们可以证明 : 对于每个前缀, 它的有效后缀数量为 $O(\log n)$.
证明
我们规定 : 以一个前缀的结束位置来命名这个前缀, 以一个后缀的起始位置来命名这个后缀. $|i|$ 表示后缀 $i$ 的长度.
对于前缀 $R$, 我们把它的有效后缀按照起始位置从小到大排序, 设 $i,j$ 为它的两个相邻有效后缀.

因为它们都有可能得到最优答案, 所以后缀 $j$ 是后缀 $i$ 的一个前缀. 有因为后缀 $j$ 是后缀 $i$ 的一个后缀, 所以后缀 $j$ 是后缀 $i$ 的一个 $border$. (图中蓝括号部分和红括号部分对应相等)
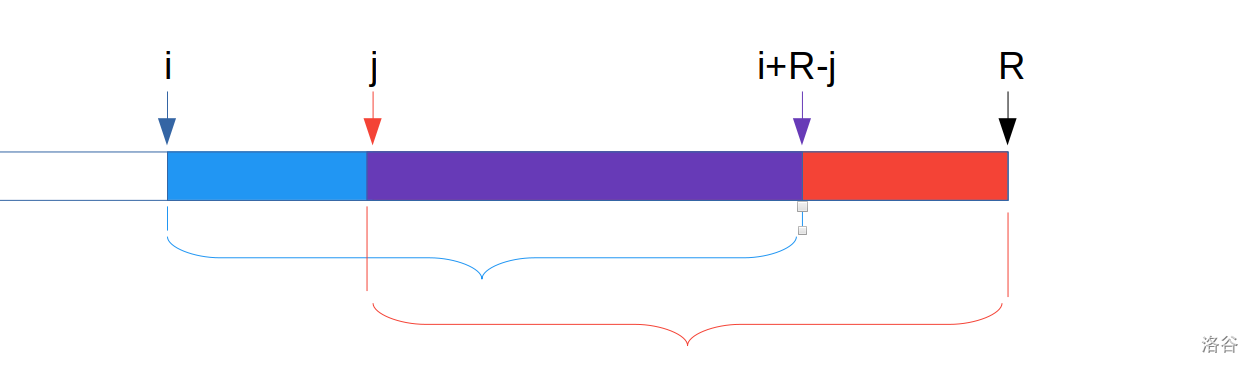
所以, 后缀 $i$ 可以用一个长度为 $j-i$ 的字符串循环表示. (图中箭头所指部分对应相等)
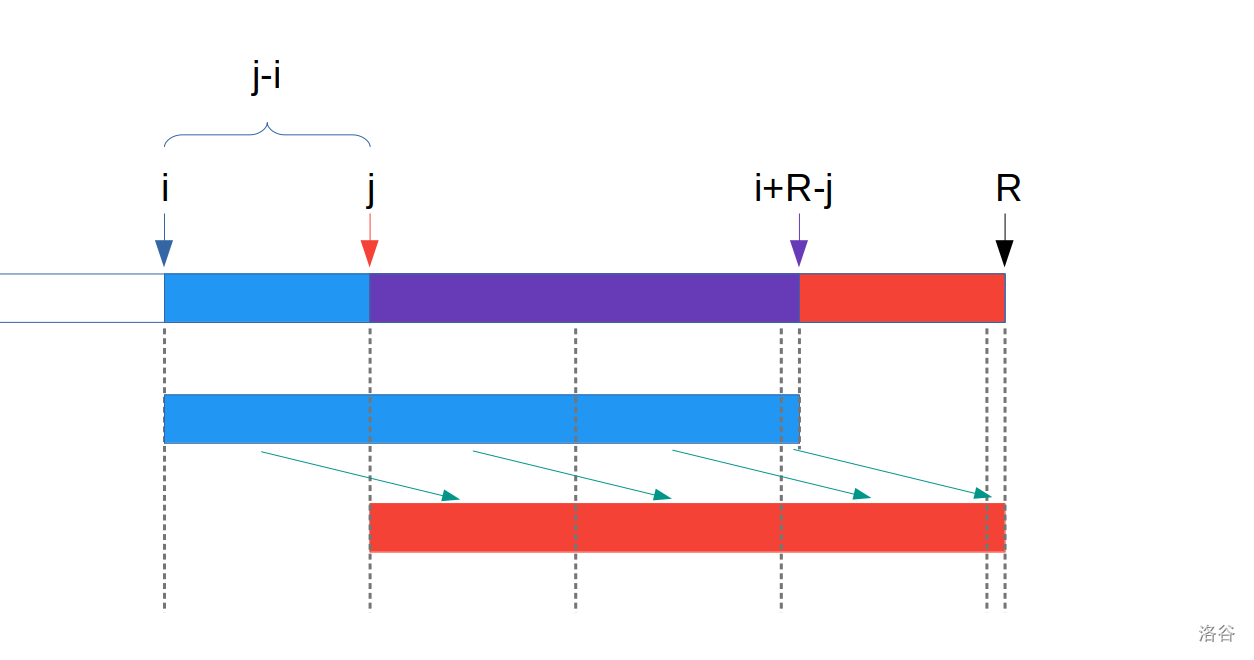
设 $k=j+(j-i)$
假设 $j$ 是前缀 $R$ 的最优解, 那么就会存在两个点 $S,T(T-S=j-i)$, 使得字符串 $[i,S] >$ 字符串 $[j,T]$. (图中分别表示为 $I,J$)
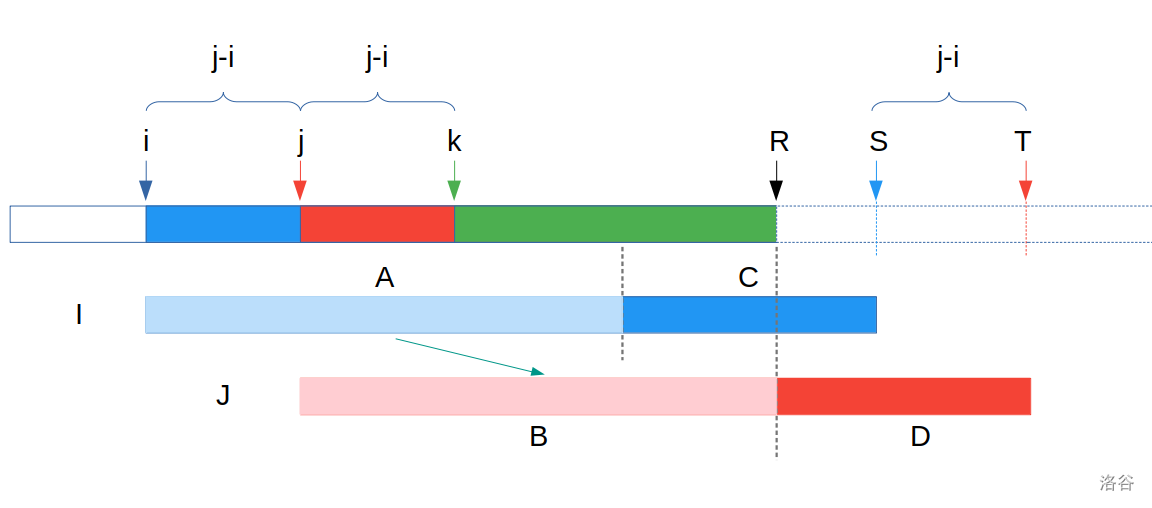
由于字符串 $A,B$ 对应相等, 所以字符串 $C>D$.
那么, 也就会使得字符串 $[j,S] > [k,T]$. (图中分别表示为 $J’,K$)
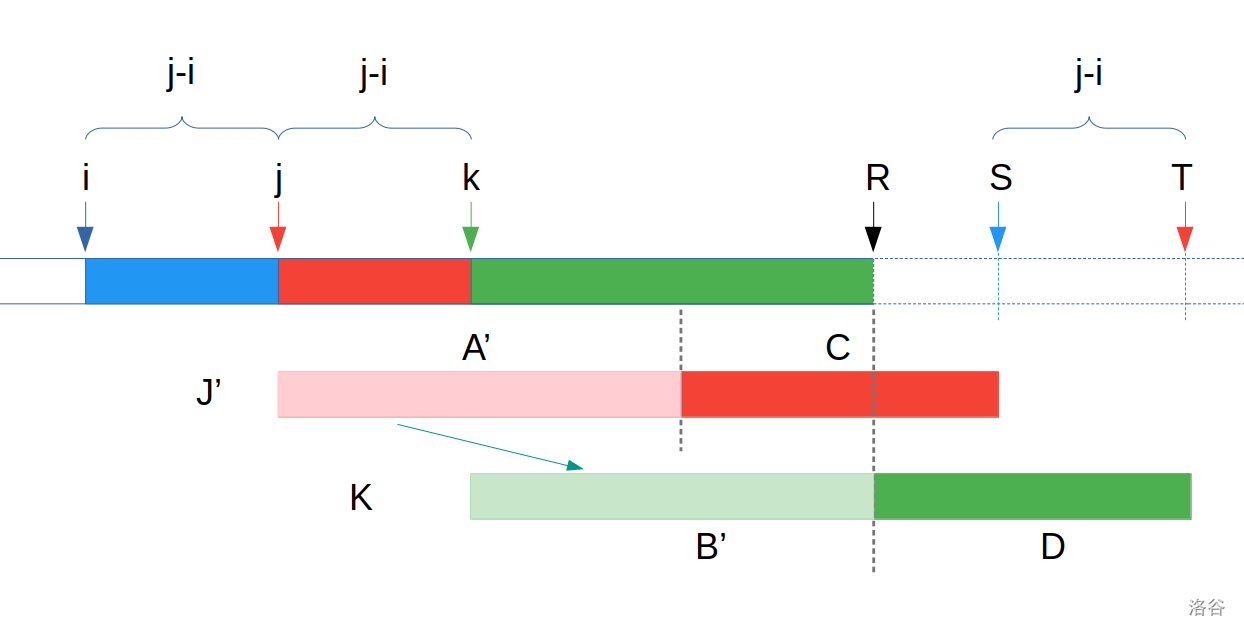
也就是说, $k$ 会代替 $j$ 成为前缀 $R$ 的最优解, 那 $j$ 就不是一个「有效后缀」, 与假设矛盾.
故, 对于前缀 $R$ 的两个相邻有效后缀 $i,j$, 必定满足 $|i| \ge |j|$. 所以前缀 $R$ 最多只会有 $\log R$ 个有效后缀.
具体实现
首先是找出有效后缀. 我们从前往后枚举 $R$, 并维护一个栈来存储当前的有效后缀, 具体见代码.
然后是找出这若干个有效后缀中的最优解. 对于两个有效后缀 $i,j\ (i<j)$, 为了比较它们的大小, 我们需要找出后缀 $i+r-j$ 与后缀 $1$ 的 $LCP$ (最长公共前缀), 然后比较它们第一位不相等的字符来决定它们的大小. 每个后缀的 $LCP$ 可以通过 $Z$ 算法 (扩展 $kmp$) 解决.
代码
#include<bits/stdc++.h>
using namespace std;
#define pb push_back
#define sz(x) (int)(x).size()
const int _=3e6+7;
int n,z[_],lst[_],num,stk[_],top;
string s;
void Z(){
int l=0,r=0;
for(int i=1;i<n;i++){
if(i<r) z[i]=min(r-i+1,z[i-l]);
while(i+z[i]<n&&s[i+z[i]]==s[z[i]]) z[i]++;
if(i+z[i]-1>r) l=i,r=i+z[i]-1;
}
z[0]=n;
}
void Init(){
cin>>s,n=s.size();
Z();
}
int Min(int &x,int y,int r){
if(!x) return y;
int t=y+r-x+1;
if(t+z[t]-1>=r) return y; // 可以证明, 当后缀 y+r-x 与后缀 1 的 LCP 延伸的长度大于等于 r 时, x 一定不是最优解
return s[t+z[t]]<s[z[t]] ?y :x;
}
void Run(){
printf("%d ",1);
lst[num=1]=0;
for(int r=1;r<n;r++){
stk[top=1]=r;
for(int i=1;i<=num;i++){
while(top&&(s[lst[i]+r-stk[top]]<s[r])) top--;
if(top&&s[lst[i]+r-stk[top]]==s[r]&&r-lst[i]+1<2*(r-stk[top]+1)) top--;
if(!top||s[lst[i]+r-stk[top]]==s[r]) stk[++top]=lst[i];
}
num=top;
int minx=0;
for(int i=1;i<=top;i++){
lst[i]=stk[i];
minx=Min(minx,stk[i],r);
}
printf("%d ",minx+1);
}
putchar('\n');
}
int main(){
#ifndef ONLINE_JUDGE
freopen("x.in","r",stdin);
freopen("x.out","w",stdout);
#endif
Init();
Run();
return 0;
}
0 条评论