【题解】薇尔莉特的打字机

update：题目地址：here

首先，这题需要处理字符串，我们用 $trie$分析

先忽略删除操作

拿样例 1 举个例子：

首先把最开始的字符串插入到树中

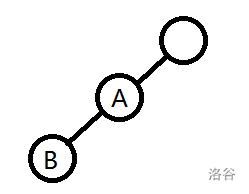
然后薇尔莉特打了一个字符 $A$

此时可以插入或者是不插入，就会有这样的情况：

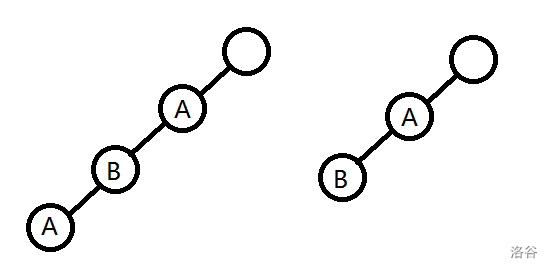
不插入时，之前插入进去的字符均可以作为字符串的结尾

假设之前插入了 $x$个字母，每一个字母都可以作为串的结尾

现在插入这个字符，总数似乎又增加了 $x$个

继续看样例 1，此时薇尔莉特又打了一个字符 $A$

此时把它插入树中，就是这样：

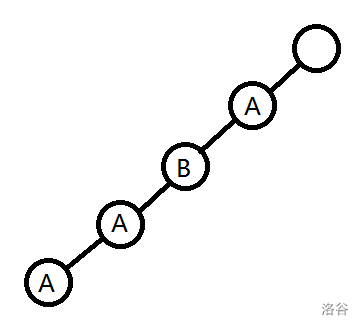
此时能作为串的结尾的数仍然只有 $A$，重复了

所以如果新产生的可以作为结尾的节点

那么没有可以作为结尾的节点和这个节点相同

可能说的有点绕，举个例子：

假如 $A$已经存在于这棵树中并且可以作为结尾

那么再插入一个 $A$不能增加可以作为结尾节点的数量

令 $ans$表示插入之前可以作为结尾节点的节点数量

新插入的字符为 $x$

$f_i$表示已经有第 $i$种字符的可以作为结尾节点的总数

我们可以算出现在的 $ans$=之前的 $ans$×$2$-$f_{ch}$，$f_{ch}$=原来的 $ans$

---

接下来是删除部分

此时我们已经插入了这几个节点：

删除的过程其实就是去掉当前节点往上跳的过程

比如说删除当前的 $A$之后就是这样：

删除了这个节点往上跳，上面的节点一定是可以作为结尾节点的节点

所以此时新产生的结果只有 1，加 1 即可

模拟 $trie$的操作，直接递推就好了

---

P.S. 看到这个题的模数有点懵，太菜了不知道是什么，于是……

然而还是布吉岛这个模数为什么这么怪 $qwq$

---

下面是代码：

#include<bits/stdc++.h>
using namespace std;
const int yyf=19260817;//日膜 yyf
int n,m;
int f[100];
char s[5000002];
int main(){
    cin>>n>>m;
    scanf("%s",s+1);                
    char ch;int ans=1;
    while(m--){
        cin>>ch;
        if(ch=='u'){                            //删除操作  
            if(!n)continue;                     //没有可以删除的了
            else{
                ans=(ans+1)%yyf;                //+1
                f[s[n]-'A']=(f[s[n]-'A']+1)%yyf;//+1
                --n;                            //删除节点往上跳
            }
        }
        else{                               
            int tmp=f[ch-'A'];                  //暂时保存
            f[ch-'A']=ans;                      //赋值
            ans=((ans+ans-tmp)%yyf+yyf)%yyf;    //算 ans
        }
    }
    cout<<ans;
    return 0;
}