不想多说什么,再次错过一次 AK 机会
T1 青蛙的烦恼
蛤の烦恼
⃢ — ⃢
设 $f(i,j,k)$为在区间 $[l,r]$内,位置为 k 时遍历所有坐标的最短路径。
$dis(i,j)$表示从点 i 到点 j 的距离
这样空间复杂度为 $n^3$,1e9 无法接受
不难发现 k 只可能为 i 或者为 j
所以设 $f(i,j,t)$为当前位置为 i,区间长度为 j。t=0 表示区间在 i 右边,t=1 表示区间在左边。
空间复杂度降到了 $n^2$
于是就轻松解决了
代码:
#include <bits/stdc++.h>
#define dis(a,b) (sqrt((x[a]-x[b])*(x[a]-x[b])+(y[a]-y[b])*(y[a]-y[b])))
using namespace std;
int n;
double x[1000],y[1000],f[1000][1000][2];
bool book[1000][1000][2];
double dfs(int cur,int l,int t)
{
if(book[cur][l][t])return f[cur][l][t];
book[cur][l][t]=1;
if(l==1)return 0;
if(!t)
f[cur][l][t]=
min(dfs(cur+l-1,l-1,1)+dis(cur,cur+l-1),dfs(cur+1,l-1,0)+dis(cur,cur+1));
else
f[cur][l][t]=
min(dfs(cur-l+1,l-1,0)+dis(cur,cur-l+1),dfs(cur-1,l-1,1)+dis(cur,cur-1));
return f[cur][l][t];
}
int main()
{
freopen("frog.in","r",stdin),freopen("frog.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%lf%lf",&x[i],&y[i]);
printf("%.3f\n",dfs(1,n,0));
return 0;
}
T2 警卫安排
我真是太弱了
没事多叉转二叉干啥
转二叉理论上也能做,只是需要讨论 4 种情况。
所以不如不转

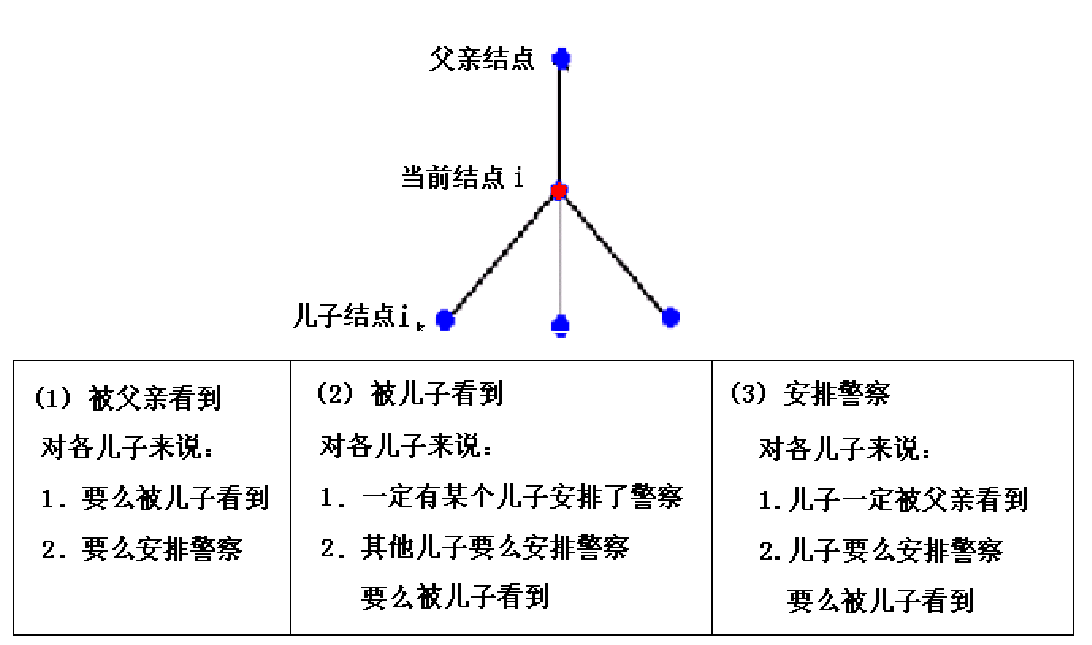

//以上截图自 ppt
下面代码中,0 表示安排警卫,1 表示被父亲看到,2 表示被儿子看到。
代码:
#include <bits/stdc++.h>
using namespace std;
int n,v[1000],root,f[1000][3];
bool book[1000];
vector<int> g[1000];
int dfs(int u,int w)
{
if(f[u][w]!=-1)return f[u][w];
switch(f[u][w]=0,w)
{
case 0:
for(int i=0;i<g[u].size();i++)
f[u][w]+=min(dfs(g[u][i],0),min(dfs(g[u][i],1),dfs(g[u][i],2)));
f[u][w]+=v[u];break;
case 1:
for(int i=0;i<g[u].size();i++)f[u][w]+=min(dfs(g[u][i],0),dfs(g[u][i],2));
break;
case 2:
f[u][w]=1e8;
for(int i=0;i<g[u].size();i++)
f[u][w]=min(f[u][w],dfs(g[u][i],0)-min(dfs(g[u][i],0),dfs(g[u][i],2)));
for(int i=0;i<g[u].size();i++)
f[u][w]+=min(dfs(g[u][i],0),dfs(g[u][i],2));
break;
}
return f[u][w];
}
int main()
{
freopen("security.in","r",stdin),freopen("security.out","w",stdout);
scanf("%d",&n);
for(int i=1,j,k;i<=n;i++)
{
scanf("%d",&j),scanf("%d%d",&v[j],&k);
for(int i1=1,j1;i1<=k;i1++)scanf("%d",&j1),g[j].push_back(j1),book[j1]=1;
}
for(int i=1;i<=n;i++)if(!book[i]){root=i;break;}
memset(f,-1,sizeof(f)),printf("%d\n",min(dfs(root,0),dfs(root,2)));
return 0;
}
T3 最长上升子序列
最水的一题。
在 1…k 跑一遍 lis,再再 k+1…n 跑一遍 lis 即可。
第二次跑 lis 的时候需要筛掉所有小于第 k 个数的元素
答案为 $f[k]+max\{f[k+1…n]\}$
也可以一开始先筛掉所有小于第 k 个数的元素,再跑一遍 lis
需要用 nlogn 的算法
代码:
#include <bits/stdc++.h>
using namespace std;
int n,k,a[200005],e[200005],cnt,f[200005],ans;
int main()
{
freopen("lis.in","r",stdin),freopen("lis.out","w",stdout);
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=k;i++)
{
f[i]=(int)(lower_bound(e+1,e+1+cnt,a[i])-e);
if(f[i]>cnt)e[++cnt]=a[i];else if(a[i]<e[f[i]])e[f[i]]=a[i];
}
memset(e,0,sizeof(e)),cnt=0;
for(int i=k+1;i<=n;i++)
if(a[i]>a[k])
{
f[i]=(int)(lower_bound(e+1,e+1+cnt,a[i])-e);
if(f[i]>cnt)e[++cnt]=a[i];else if(a[i]<e[f[i]])e[f[i]]=a[i];
ans=max(ans,f[i]);
}
printf("%d\n",ans+f[k]);
return 0;
}
T4 最短回文串
区间 dp
设 $f(i,j)$为把 $[i,j]$这段子串变为一个回文串的最小代价
当 $s[i]==s[j]$时 $f(i,j)=f(i+1,j-1)$
否则 $f(i,j)=min\{f(i+1,j),f(i,j-1)\}+1$
代码:
#include <bits/stdc++.h>
using namespace std;
int n,f[5005][5005];
char s[5005];
int main()
{
freopen("palindrome.in","r",stdin),freopen("palindrome.out","w",stdout);
scanf("%d%s",&n,s);
for(int l=1;l<n;l++)
for(int i=0;i+l<n;i++)
{
f[i][i+l]=min(f[i+1][i+l],f[i][i+l-1])+1;
if(s[i]==s[i+l])f[i][i+l]=min(f[i][i+l],f[i+1][i+l-1]);
}
printf("%d\n",f[0][n-1]);
return 0;
}
0 条评论