题意：

给你数轴上的两个点 X,Y，你有６中走法，分别是从 X 向各个方向走 a 个单位、b 个单位、(a+b) 个单位。求最少要走几步走到 Y。

思路：

令步数为 T，其中向左走 a 个单位 p 次，b 个单位 q 次 (p,q 可以为负数) 则有：
$$ T=
\begin{cases}
|p|+|q| & \text{pq\textless =0} \\
max(|p|,|q|) & \text{pq\textgreater 0}
\end{cases}
$$
那么我们只需要用扩展欧几里德算法求出 p,q 的特解 p0,q0，再计算什么 p,q，可以让 T 取得最小值。
首先，为了让你走到 X，则有：
$$
p_0\times a + q_0\times b = Y-X
$$
由扩展欧几里德算法：
$$
\begin{cases}
p = p_0 + t\times \frac{b}{gcd(a,b)} \\
q = q_0 – t\times \frac{a}{gcd(a,b)}
\end{cases}
$$
所以我们发现 p 和 q 都可以表示为关于 t 的直线，且这两条直线的斜率一正一负，他们必定有一个交点。
所以我们不妨画出这个图像。


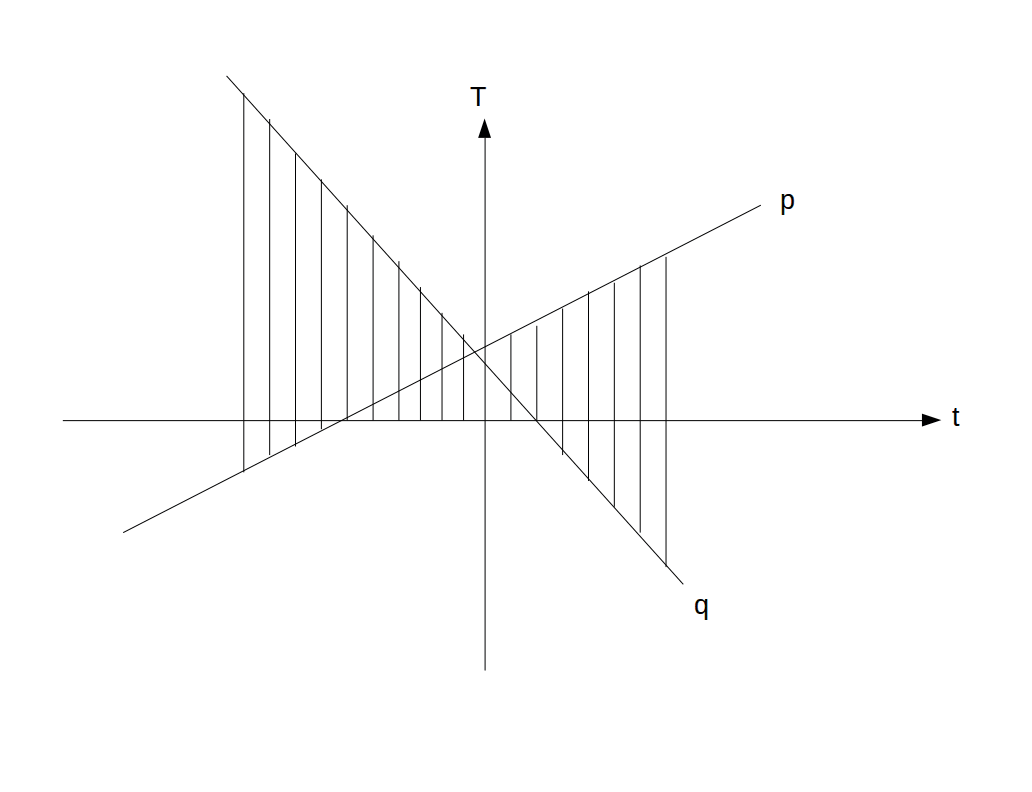
其中阴影部分的竖线长度就是 T，是不是很直观？
所以我们需要求出这两条线的交点。由于这两条直线不一定橡胶于整点，所以我们需要计算交点及其周围的竖线长度。于是这道题就没了。

#include <iostream>
#include <cstdio>
#include <cmath>

#define labs(a) (a>0?a:-a)

using namespace std;

typedef long long ll;

ll eu(ll x,ll y,ll &p,ll &q)
{
    if(y==0)
    {
        p=1,q=0;
        return x;
    }
    int rt=eu(y,x%y,p,q);
    p=p-q*(int)(x/y);
    swap(p,q);
    return rt;
}

ll work(ll x,ll y,ll a,ll b)
{
    ll g,p,q,tmp=9999999999999999;
    g=eu(a,b,p,q);
    if((y-x)%g!=0){return -1;}
    ll p1=p*(y-x)/g,q1=q*(y-x)/g;
    ll dp=b/g,dq=a/g;
    ll tt=(q1-p1)/(dp+dq);
    for(int i=tt-1;i<=tt+1;i++)
    {
        p=p1+i*dp,q=q1-i*dq;
        if((p<0&&q>0)||(p>0&&q<0))tmp=min(tmp,labs(p)+labs(q));
        else tmp=min(tmp,max(labs(p),labs(q)));
    }
    return tmp;
}

int main()
{
    int t;
    ll x,y,a,b;
    scanf("%d",&t);
    for(int w=1;w<=t;w++)
    {
        scanf("%lld%lld%lld%lld",&x,&y,&a,&b);
        cout<<work(x,y,a,b)<<endl;
    }
    return 0;
}