卡常神题
多重背包最基本的状态转移方程是这样的: 用 f[i][j] 表示前 i 个物品装进背包占容量为 j 时的最大价值。
$$
f[i][j]=max(f[i-1][j-k\times w[i]]+k\times v[i]) (0<=k<=c[i])
$$
但是我们有一个经常会问的问题:能不能更快些?
答案几乎都是:可以
题意:
求用 n 种硬币每种 c[i] 个最多可以凑出多少种面额?
二进制优化:
作为将 $O(NV\sum{\frac{V}{w[i]}})$也就是 $O(N^2V)$级别的算法优化成 $O(V\sum{log(c[i])})$的方法,自然少不了对”2″ 灵活的应用。
由于这种方案的优化效果不是非常好,无法顺利通过本题,而且大家肯定已经可以熟练运用,这里暂不讨论。
单调队列优化:
$O(K\times logN)$的算法再经过某些基于单调性的脑洞级优化后,会变成惊人的 $O(K\times 1)$而这道题用到的当然就是这种方法。
观察 f[i][j] 是由哪些东西的最小值转移过来的:
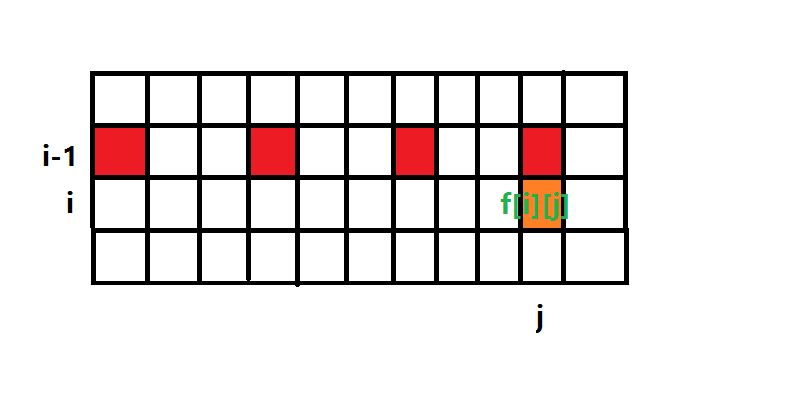
所以,对于这道题,我们要知道的就是红色格子里有没有可以达到的容量。而红色格子是连续的最多 c[i] 个。
这不是 so-easy 的东西吗?
下面具体介绍几种解决方法:
1.
我们建立一个假的队列,这个队列有队首和队尾,但是没有队列元素。
现在我们从 f[i-1][0] 向 f[i-1][j] 每隔 w[i] 个将那个数添加到队列中,用队列记录队首到队尾的和。这样对于 f[i][j],队列中的所有元素的和就是我们图片中红色格子的和。
2.
不用建立队列,并且将方程的维数降为 1 维。这时转移方程就是:(f[j] 表示达成 j 容量的方案数。)
for(int i=1;i<=n;i++)
{
for(int j=v[i];j<=V;j++)
f[j]=f[j]+f[j-v[i]];
for(int j=v[i];j<=V;j++)
if(j-(c[i]+1)*w[i]>=0)f[j]-=f[j-(c[i]+1)*w[i]];
}
这就是完全背包的做法再减去不应该装的物品的做法。程序结束后 f[i] 数组里留下来的就是达成 i 容量的方案数。但是由于第二层循环需要 2 次,这种方法还是会莫名其妙就 TLE。。。
3.
借鉴于第二种方法,我们可以再开辟一个数组 s[j] 表示 f[j] 是装了多少件 i 物品从而变为可行的。总之这样就可以 AC
for(srg int i=1;i<=n;i++)
{
memset(s,0,sizeof(s));
for(srg int j=v[i];j<=mv;j++)
{
if(!f[j]&&f[j-v[i]]&&s[j-v[i]]<c[i])
{
++tot;
f[j]=1;
s[j]=s[j-v[i]]+1;
}
}
}
那么我通过此题的代码如下:(应用了诸多卡常技巧)
#include <iostream>
#include <cstdio>
#include <cstring>
#define MX 110
#define srg register
using namespace std;
int v[MX],c[MX];
int f[100010];
int s[100010];
int n,mv,tot;
int main()
{
while(scanf("%d %d", &n, &mv) && n && mv >= 0)
{
for(srg int i=1;i<=n;i++)scanf("%d",&v[i]);
for(srg int i=1;i<=n;i++)scanf("%d",&c[i]);
for(srg int i=0;i<=mv;i++)f[i]=0;
f[0]=1,tot=0;
for(srg int i=1;i<=n;i++)
{
memset(s,0,sizeof(s));
for(srg int j=v[i];j<=mv;j++)
if(!f[j]&&f[j-v[i]]&&s[j-v[i]]<c[i])
++tot,f[j]=1,s[j]=s[j-v[i]]+1;
}
printf("%d\n",tot);
}
return 0;
}
3 条评论
konnyakuxzy · 2017年7月17日 10:12 下午
boshi 大佬您忘记放代码啦
konnyakuxzy · 2017年7月18日 10:57 上午
好吧您已经放好啦。。。
但是为什么您不写
快读
呢?
boshi · 2017年7月18日 1:51 下午
我的快读会让我 WA