1. 题目

传送门=￣ω￣=

2. 题解

写完才发现原来正方形的边不一定平行于 x 或 y 轴。。。
首先无图言 diao：

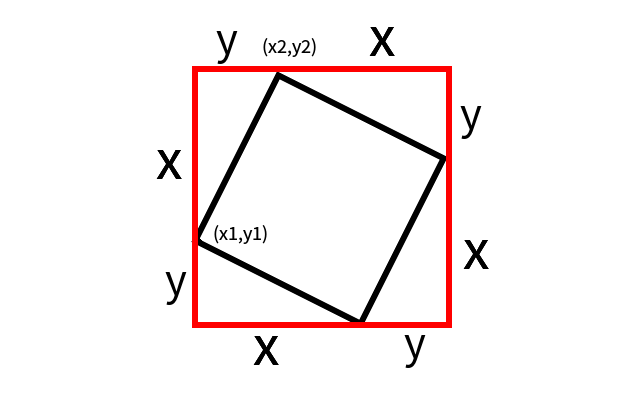
如图，设正方形左上角的点的坐标是 (x1,y1)，右上角的点是 (x2,y2)
那么 y=x2-x1,x=y2-y1，那么很显然，左下角的点的坐标是 (x1+x,y1-y)，右下角的点的坐标是 (x2+1,y2-y)。
所以我们枚举所有的斜率>=0 且不平行于 y 轴的线段（即枚举任意两个满足 x1<x2 且 y1<y2 的点），也就是图中的 (x1,y1) 和 (x2,y2)，再查哈希表，如果 (x1+x,y1-y) 还有 (x2+1,y2-y) 这两个坐标都有点存在的话，就有一个存在的正方形。
这样因为我们只枚举每个正方形的左上的边，所以答案不会有重复。

代码：

#include <cstdio>
#include <set>
#define MKP make_pair
using namespace std;
typedef pair<int,int> PII;
int n,ans,x[1005],y[1005];
set<PII> SET;
int main()
{
    while(scanf("%d",&n),n)
    {
        for(int i=1,a,b;i<=n;i++)
            scanf("%d%d",&x[i],&y[i]),SET.insert(MKP(x[i],y[i]));
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
            {
                int x1=x[i],y1=y[i],x2=x[j],y2=y[j],dx,dy;
                if(x1>=x2||y1>y2)continue;
                dx=x2-x1,dy=y2-y1;
                ans+=SET.count(MKP(x1+dy,y1-dx))&&SET.count(MKP(x2+dy,y2-dx));
            }
        printf("%d\n",ans);
        ans=0,SET.clear();
    }
    return 0;
}