1. 二分图最大匹配的定义

二分图匹配的定义：

给定一个二分图 G，在 G 的一个子图 M 中，M 的边集 {E} 中的任意两条边都不依附于同一个顶点，则称 M 是一个匹配。——百度百科

---

---

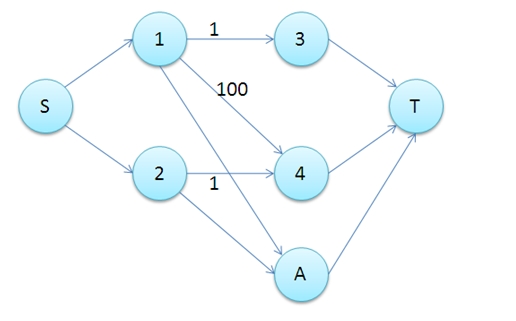
而二分图最大匹配就是这个二分图中所有匹配中边数最多的那个匹配。

2. 思路——DFS

就是枚举没有在当前的匹配中的点，寻找新的增广路（←戳这里看定义）。
求一个二分图的最大匹配的做法：
1. 读入二分图
2. 循环下面这个过程：
1. 选则一个没有匹配的点，再枚举与这个点相邻的点。
2. 如果当前枚举的这个点未配对，那就使当前选中的点和当前枚举的点匹配成一对，并返回找增广路成功。
3. 如果当前枚举的点配对了，那么我们就判断能否使与当前枚举的点配对的点与另一个点配对，如果可以就使当前选中的点和当前枚举的点匹配成一对，并返回找增广路成功。
4. 否则就跳过当前枚举的点
5. 如果所有相邻的点都枚举完了，返回找增广路失败。
6. 对于每次得到的返回值，如果使成功就让二分图匹配的大小+1，否则不变。

最后输出二分图匹配大小。

3. 模板题&代码

二分图二•二分图最大匹配之匈牙利算法 HihoCoder – 1122

戳这里→传送门

#1122 : 二分图二•二分图最大匹配之匈牙利算法

时间限制:10000ms
单点时限:1000ms
内存限制:256MB

描述

上一回我们已经将所有有问题的相亲情况表剔除了，那么接下来要做的就是安排相亲了。因为过年时间并不是很长，所以姑姑希望能够尽可能在一天安排比较多的相亲。由于一个人同一天只能和一个人相亲，所以要从当前的相亲情况表里选择尽可能多的组合，且每个人不会出现两次。不知道有没有什么好办法，对于当前给定的相亲情况表，能够算出最多能同时安排多少组相亲呢？

同样的，我们先将给定的情况表转换成图 G=(V,E)。在上一回中我们已经知道这个图可以被染成黑白两色。不妨将所有表示女性的节点记为点集 A，表示男性的节点记为点集 B。则有 A∪B=V。由问题可知所有边 e 的两个端点分别属于 AB 两个集合。则可以表示成如下的图：

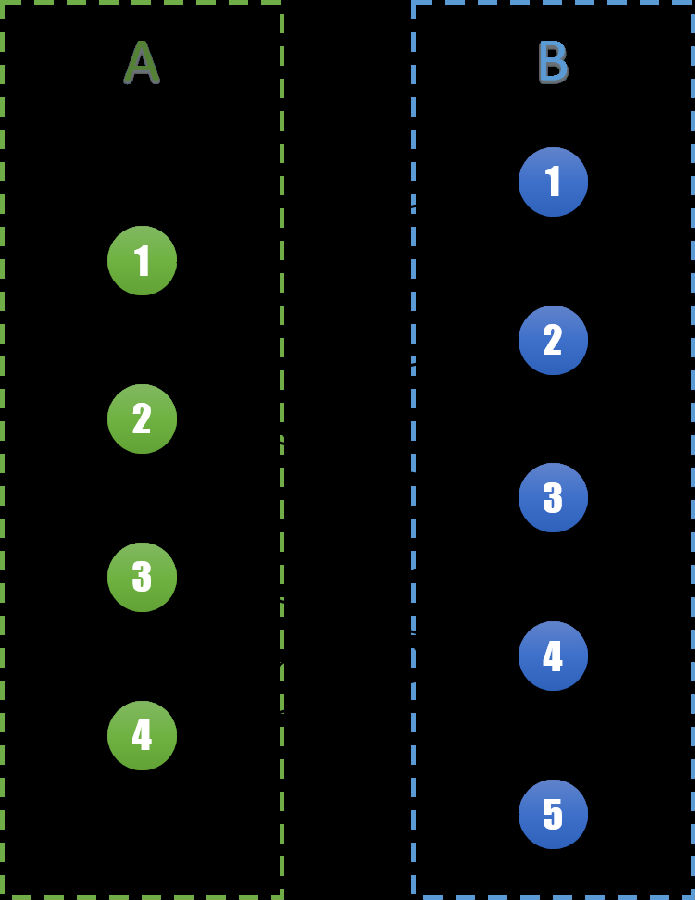
同样的，我们将所有的边分为两个集合。集合 S 和集合 M，同样有 S∪M=E。边集 S 表示在这一轮相亲会中将要进行的相亲，边集 M 表示在不在这一次进行。对于任意边 (u,v) ∈ S，我们称 u 和 v 为一组匹配，它们之间相互匹配。在图 G，我们将边集 S 用实线表示，边集 M 用虚线表示。得到下图：

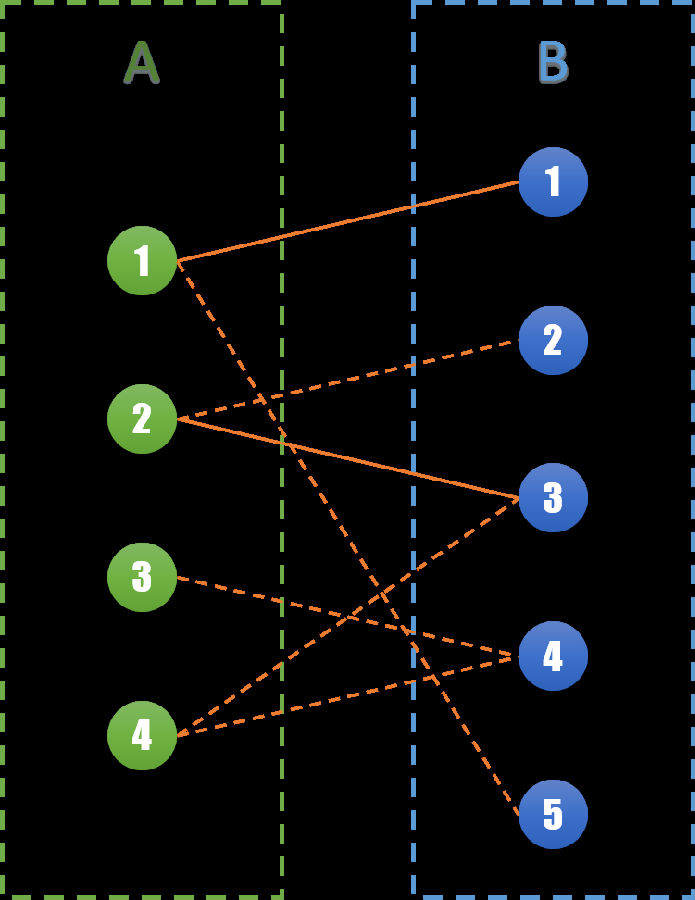
则原问题转化为，最多能选择多少条边到集合 S，使得 S 集合中任何两条边不相邻 (即有共同的顶点)。显然的，|S|<=Min{|A|, |B|}。

那么能不能找到一个算法，使得能够很容易计算出尽可能多的边能够放入集合 S？我们不妨来看一个例子：

对于已经匹配的点我们先不考虑，我们从未匹配的点来做。这里我们选择 A 集合中尚未匹配的点 (A3 和 A4) 考虑：

对于 A3 点，我们可以发现 A3 与 B4 右边相连，且都未匹配。则直接将 (A3,B4) 边加入集合 S 即可。

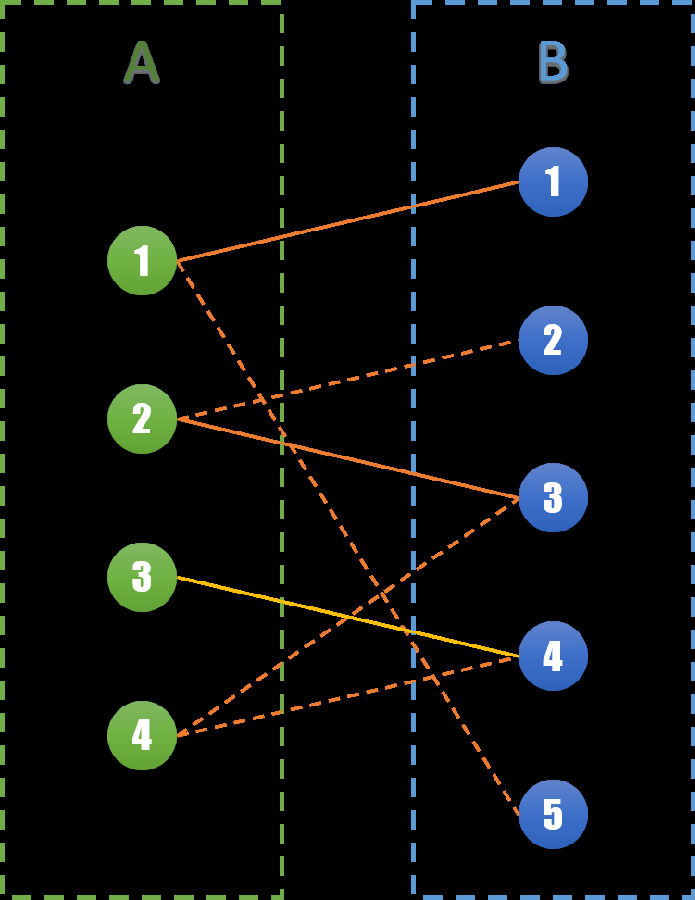
对于 A4 点，我们发现和 A4 相连的 B3，B4 点都已经匹配了。但是再观察可以发现，如果我们将 A2 和 B2 相连，则可以将 B3 点空出来。那么就可以同时将 (A2,B2)，(A4,B3) 相连。将原来的一个匹配变成了两个匹配。

让我们来仔细看看这一步：我们将这次变换中相关联的边标记出来，如下图所示紫色的 3 条边 (A2,B2),(A2,B3),(A4,B3)。

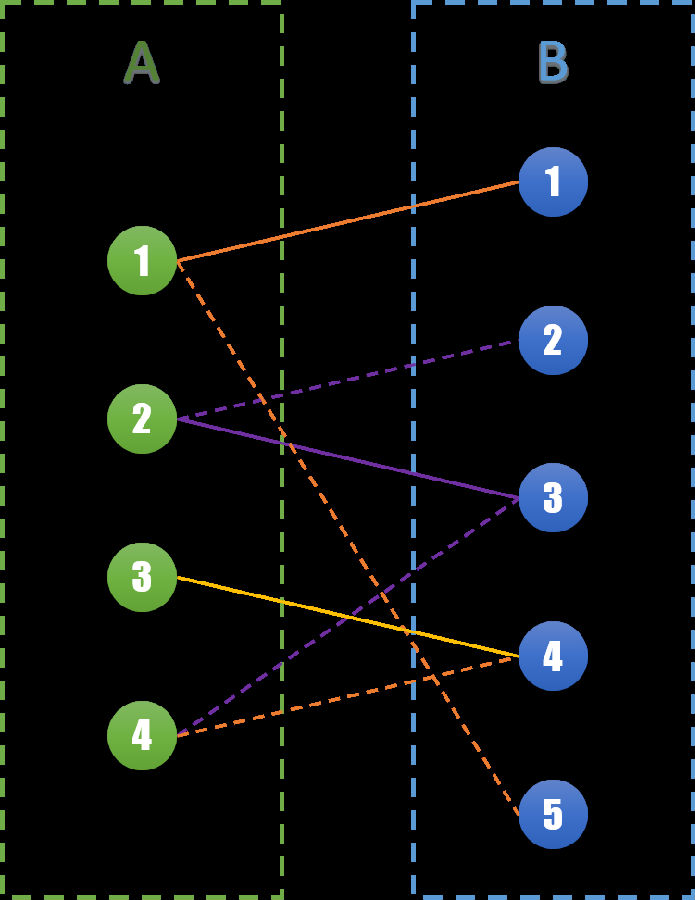
这三条边构成了一条路径，可以发现这条路径有个非常特殊的性质。虚线和实线相互交错，并且起点和终点都是尚未匹配的点，且属于两个不同的集合。我们称这样的路径为交错路径。

再进一步分析，对于任意一条交错路径，虚线的数量一定比实线的数量多 1。我们将虚线和实线交换一下，就变成了下面的图：

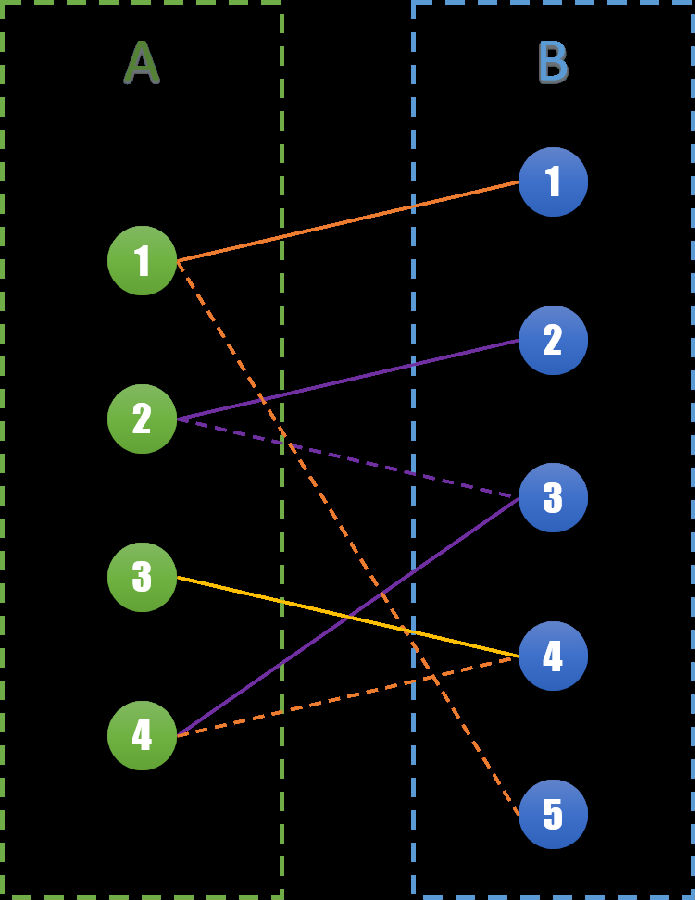
在原来 1 个匹配的基础上，我们得到了 2 个新的匹配，S 集合边的数量也增加了 1。并且原来在已经匹配的点仍然是已经匹配的状态。

再回头看看 A3 点匹配时的情况：对于 (A3,B4) 这一条路径，同样满足了交错路径的性质。

至此我们得到了一个找新匹配的有效算法：

选取一个未匹配的点，查找是否存在一条以它为起点的交错路径。若存在，将该交错路径的边虚实交换。否则在当前的情况下，该点找不到可以匹配的点。

又有对于已经匹配的点，该算法并不会改变一个点的匹配状态。所以当我们对所有未匹配的点都计算过后，仍然没有交错路径，则不可能找到更多的匹配。此时 S 集合中的边数即为最大边数，我们称为最大匹配数。

那么我们再一次梳理整个算法：

1. 依次枚举每一个点 i；
2. 若点 i 尚未匹配，则以此点为起点查询一次交错路径。

最后即可得到最大匹配数。

在这个基础上仍然有两个可以优化的地方：

1. 对于点的枚举：当我们枚举了所有 A 中的点后，无需再枚举 B 中的点，就已经得到了最大匹配。
2. 在查询交错路径的过程中，有可能出现 Ai 与 Bj 直接相连，其中 Bj 为已经匹配的点，且 Bj 之后找不到交错路径。之后又通过 Ai 查找到了一条交错路径 {Ai,Bx,Ay,…,Az,Bj} 延伸到 Bj。由于之前已经计算过 Bj 没有交错路径，若此时再计算一次就有了额外的冗余。所以我们需要枚举每个 Ai 时记录 B 集合中的点是否已经查询过，起点不同时需要清空记录。

伪代码：

Function FindPath(u)

        For v∈u 的相邻节点
             标记 v 已经查询过
             If v 未匹配 or FindPath(v 的匹配的点) Then
                        更改 u 的匹配为 v
                        Return Ture
                End If
        End For
Return False

For i ∈ V
        清空标记
     FindPath(i)
End If

输入

第 1 行：2 个正整数，N,M(N 表示点数 2≤N≤1,000，M 表示边数 1≤M≤5,000)
第 2..M+1 行：每行两个整数 u,v，表示一条无向边 (u,v)
输出

第 1 行：1 个整数，表示最大匹配数
样例输入

5 4
3 2
1 3
5 4
1 5

样例输出
2

代码：

#include <iostream>
#include <vector>
using namespace std;
int n,m,ans,match[1005];
bool book[1005];
vector<int> g[1005];
bool dfs(int u)
{
    for(vector<int>::iterator i=g[u].begin();i!=g[u].end();i++)
        if(!book[*i])
        {
            book[*i]=1;
            if(match[*i]==0||dfs(match[*i])){match[u]=*i,match[*i]=u;return 1;}
        }
    return 0;
}
int main()
{
    ios::sync_with_stdio(0);
    cin>>n>>m;
    for(int i=1,u,v;i<=m;i++)cin>>u>>v,g[u].push_back(v),g[v].push_back(u);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)book[j]=0;
        if(!match[i])if(dfs(i))ans++;
    }
    cout<<ans<<endl;
    return 0;
}