1. 序言

求矩形面积并指的是给你 n 个矩形的顶点坐标（矩形的边必然平行于坐标轴），求它们所覆盖的总面积（重叠覆盖的面积只算一次覆盖）。
暴力枚举矩形的话如果 n 较大显然会超时。这时候我们就需要一种新算法：扫描线。这种算法求矩形面积并的复杂度是 nlogn 的。

2. 例题

HDU – 1542 Atlantis 传送门=￣ω￣=
题目大意：给出 n 个矩形（矩形顶点左边可能为小数）1<=n<=100，求这些矩形覆盖的面积大小（多次覆盖同一个地方只算一次覆盖），即求这些矩形的面积并。含多组数据

3. 详解

典型的求矩形面积并的题目。
对于题目的样例：

2
10 10 20 20
15 15 25 25.5
0

它的图像是这样的：

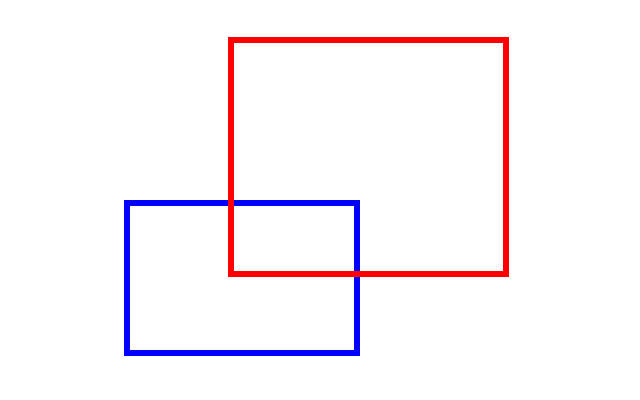
答案便是下图中黄色部分的面积：

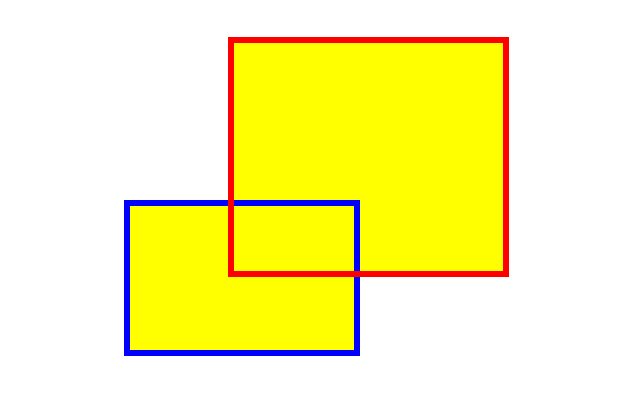
其中有一个重叠部分。

我们现在要用扫描线解决这张图。
首先我们对每个竖线的横坐标进行离散化：

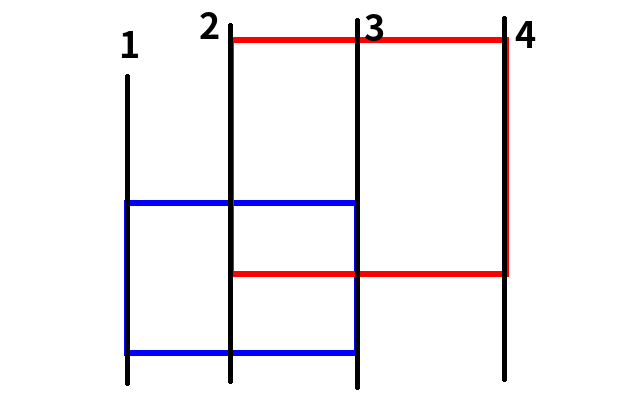
（上图中黑线表示了一个纵轴，黑线旁边的那个数字表示这个纵轴的横坐标。）

这样我们就等于把数据变成了：

2
1 10 3 20
2 15 4 25.5
0

注意上面数据中的粗体数字，表示横坐标是经过离散化的。

为什么要离散化呢？因为啊，你不离散化，把小数的横坐标变成整数，你后面怎么线段树维护啊？

我们把离散化以后的坐标存到一个 hash 表里，hash[a] 表示排第 a 个的横坐标的值是多少。比如上面那个数据中，hash[1]=10，hash[2]=15，hash[3]=20，hash[4]=25.5。hash 的同时要记得去重。

这样我们就通过这些离散化以后的横坐标把整个总区间分成了 cnt-1 个区间，其中 cnt 表示去重以后横坐标的个数，上面的样例中，cnt=4。如图：

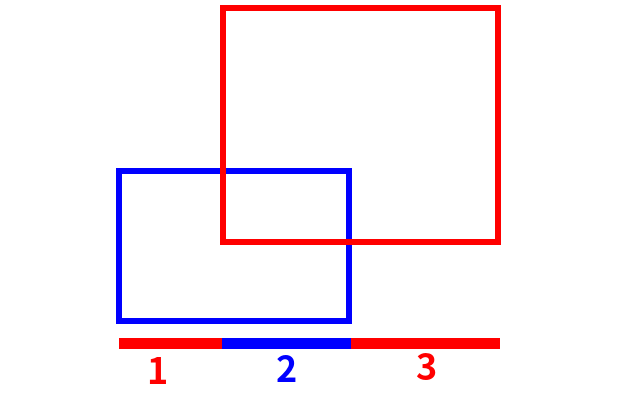
第 a 个区间的左端点的横坐标是 h[a]，右端点的横坐标是 h[a+1]。

于是我们对于这 cnt-1 个区间建立线段树。
为什么要建立线段树呢？我们等下讲。

这时候我们的重头戏来了：扫描线！
我们取出每个矩形的上边和下边，下边标为红色，上边标为蓝色。如图：

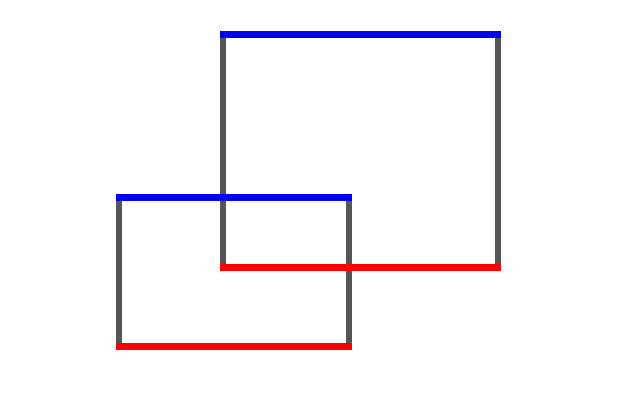
然后我们的扫描线从下向上扫描，此时每个区间的被覆盖次数都为 0，如图：

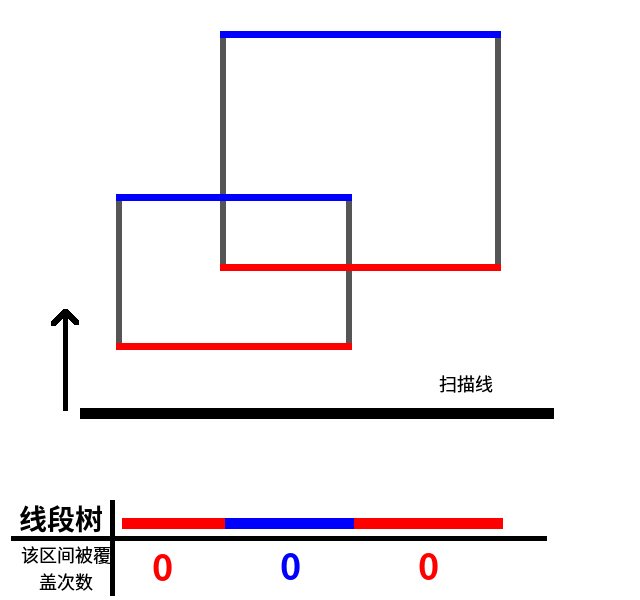
好，我们的扫描线向上移动的时候碰到了一个下边！这个下边对应线段树上的区间 1 和区间 2, 因为这是个下边，所以这两个区间在线段树上的 “被覆盖次数” 都+1 变为了 1.

我们保存一下这个扫描线的位置（纵坐标），然后扫描线继续向上移动到下一条边。。。好，扫描到了！如图所示：

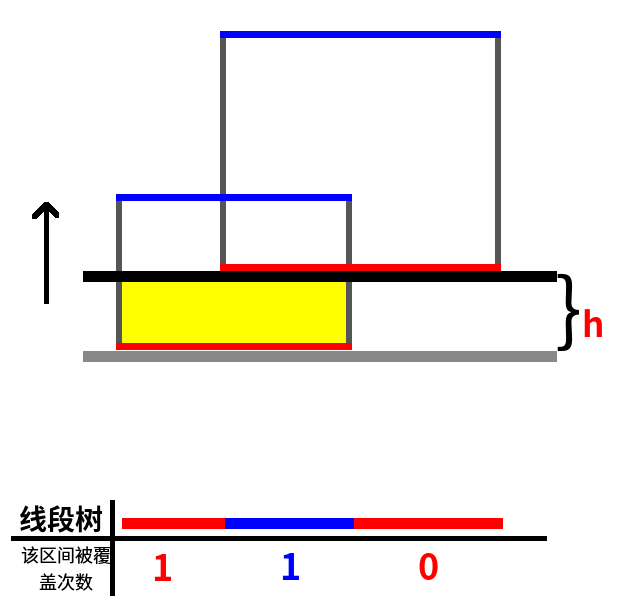
上一条保存的扫描线到当前扫描线的距离为 h=15-10=5，而总区间被覆盖了的区间有区间 1、2，这两个区间的总长度是 (20-10=10)，所以图中黄色部分的面积为 10h。那么我们让答案加上 10h=50。当前答案为 50。
又因为这是一条下边，所以区间 2，3 的被覆盖次数+1，如图所示：

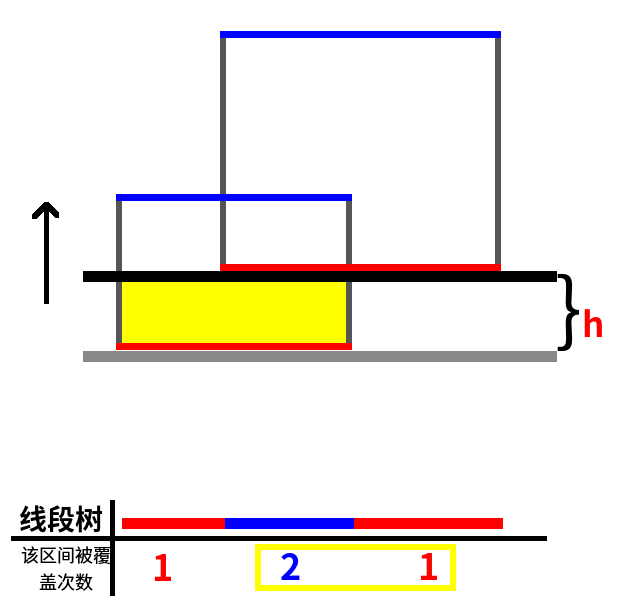
扫描线继续向上走，这次碰到的边是一条上边。如图：

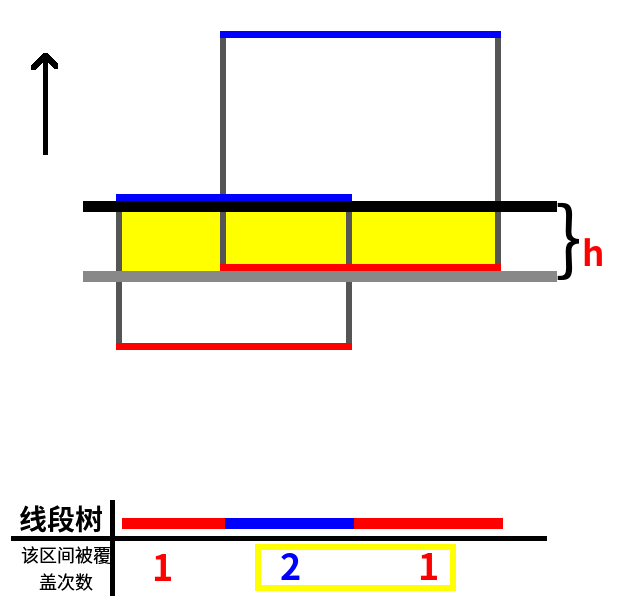
当前线段树被覆盖的区间有区间 1、2、3，所以被覆盖长度为 (25-10=15)，h=20-15=5，所以黄色部分的面积为 15h=75，答案加上 75，当前答案为 125。
因为这是一条上边，所以区间 1、2 的被覆盖次数-1，如图所示：

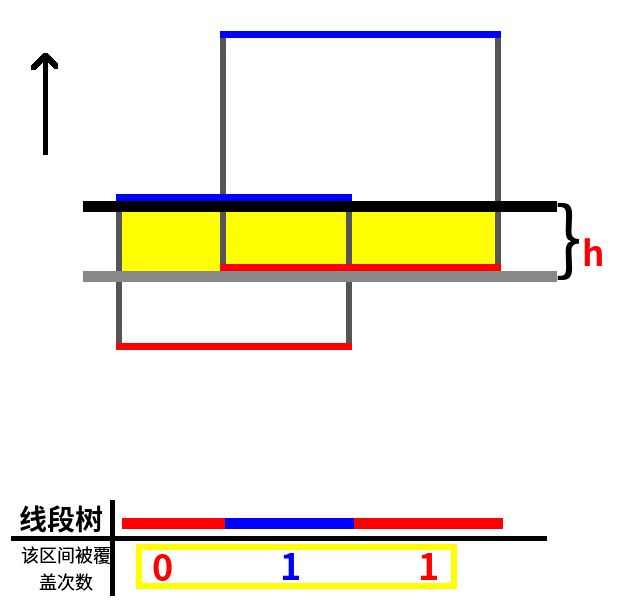
扫描线继续上移，碰到一条上边。如图：

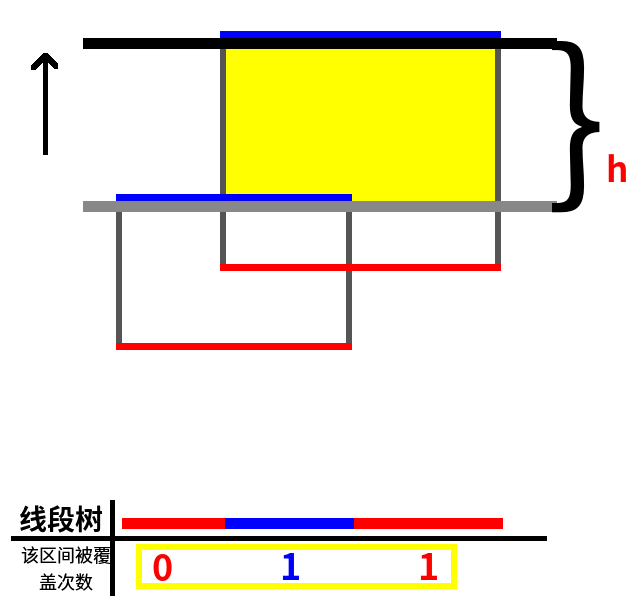
当前线段树被覆盖的区间有区间 2、3，所以被覆盖长度为 (25-15=10)，h=25.5-20=5.5，所以黄色部分的面积为 10h=55，答案加上 55，当前答案为 180。

至此我们已经得到了正确答案：180，而因为当前这条边是上边，所以区间 2、3 被覆盖次数-1，所以所有区间的覆盖次数全部为 0 了。

回头看整个过程，其实就是把这个不规则的矩形面积并分成了这几个部分：

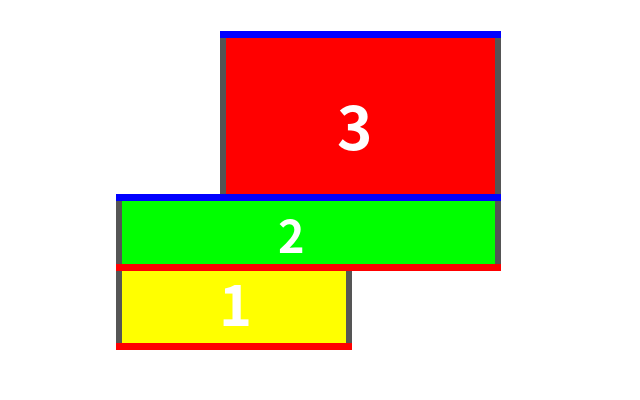
这里并没有体现出线段树的用处。显然这些操作都是区间加减：遇到下边+1，遇到上边-1，用线段树可以做到 logn。

这里的区间覆盖不需要打懒惰标记。为什么呢？因为很显然，每个下边都有与之对应的上边，它显然不会被比它的长度小的上边给清除。而如果有比它长的上边，也一定有和那个上边对应的下边还存在。所以用那个上边清除下边的时候，一定会先递归到那个更长的下边，还没有递归到它就停止递归了。所以每个上下边是一一对应的，无需下传标记等。

至于每个区间的被覆盖长度len，取决于它的被覆盖次数x。如果x>0，说明它被整体覆盖，len 就等于该区间长度。如果 x=0，那 len 等于它的左儿子区间的 len+右儿子区间的 len。

还有扫描线的上移，就是把那些上边、下边按照纵坐标大小从小到大排序即可。

其实扫描线是从下向上，或者从左到右，还是别的方向，都是一个原理，改一下离散化、区间加减就行了。

那么这道题的代码就是：

#include <bits/stdc++.h>
#define LS(a) (a<<1)
#define RS(a) ((a<<1)|1)
using namespace std;
int n,n2,cnt;
double h[205],lst,ans;
struct edge{double x1,x2,y;bool st;}e[205];
bool cmp(edge a,edge b){return a.y<b.y;}
struct N{int s,l,r;double len;}t[1005];
void build(int l,int r,int a)
{
    t[a].l=l,t[a].r=r,t[a].len=t[a].s=0;
    if(l==r)return;
    build(l,(l+r)>>1,LS(a)),build(((l+r)>>1)+1,r,RS(a));
}
void pup(int a)
{
    if(t[a].s)t[a].len=h[t[a].r+1]-h[t[a].l];
    else if(t[a].l==t[a].r)t[a].len=0;
    else t[a].len=t[LS(a)].len+t[RS(a)].len;
}
void update(double l,double r,int d,int a)
{
    if(l<=h[t[a].l]&&h[t[a].r+1]<=r){t[a].s+=d,pup(a);return;}
    if(l<h[t[LS(a)].r+1])update(l,r,d,LS(a));
    if(r>h[t[RS(a)].l])update(l,r,d,RS(a));
    pup(a);
}
int main()
{
    int T=0;
    while(scanf("%d",&n),n)
    {
        ans=cnt=0,T++,memset(h,-127,sizeof(h));
        double x1,y1,x2,y2;n2=n<<1;
        for(int i=1;i<=n2;i+=2)
        {
            scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
            e[i].x1=x1,e[i].x2=x2,e[i].y=y1,e[i].st=1;
            e[i+1].x1=x1,e[i+1].x2=x2,e[i+1].y=y2,e[i+1].st=0;
            h[i]=x1,h[i+1]=x2;
        }
        sort(h+1,h+1+n2),sort(e+1,e+1+n2,cmp);
        for(int i=1;i<=n2;i++)if(h[i]!=h[i-1])h[++cnt]=h[i];
        build(1,cnt-1,1),lst=e[1].y;
        for(int i=1;i<=n2;i++)
        {
            ans+=(e[i].y-lst)*t[1].len,lst=e[i].y;
            if(e[i].st)update(e[i].x1,e[i].x2,1,1);
            else update(e[i].x1,e[i].x2,-1,1);
        }
        printf("Test case #%d\nTotal explored area: %.2f\n\n",T,ans);
    }
    return 0;
}