曼哈顿距离
我们通常所指的距离是欧拉距离,这种距离体系很好的满足了三角形不等式,也合理地体现了空间中距离的大小关系。但是这一类距离在某些场合,甚至实际生活中却不太适用。

如图为美国纽约曼哈顿,在这里,距离的定义大概是 $dis(A,B)=\abs{A_x-B_x}+\abs(A_y-B_y)$,因为你只能沿着横平竖直的马路行进。曼哈顿距离的名称也从此而来。
衡量一个距离的定义是否合理,我们一般要检测它是否满足三角形不等式,如:
对于欧拉距离:$$dis(A,B)=\sqrt{(A_x-B_x)^2+(A_y-B_y)^2}<=dis(A,C)+dis(B,C)$$
对于曼哈顿距离:$$dis(A,B)=|A_x-B_x|+|A_y-B_y|<=dis(A,C)+dis(B,C)$$
现在我们已经确定了这种距离的定义是合理的,但是还要注意,
在考虑曼哈顿距离的同时,我们需要注意一下几点:
1. 欧拉距离在进行了坐标系的线性变换之后依然不变,但是曼哈顿距离却会随坐标轴的方向变化。几种情况例外,就是当反转 x 轴或 y 轴,以及交换 x,y 轴时。
2. 到某个点曼哈顿距离相同的点的集合是一个斜的正方形。这个结论在思考和分析过程中非常有用。
曼哈顿距离生成树
对于平面上的两个点,如果用最短的平行于坐标轴的折线连接,折线的长度就是这两个点的曼哈顿距离。
对于平面上的多个点,选取适当的点以上述折线连接,使得所有点联通,构成这些点的曼哈顿距离生成树。
折线总长度最小的曼哈顿距离生成树叫做曼哈顿距离最小生成树。
如何求出曼哈顿距离生成树呢?
最简单的想法是:先将平面上的 n 个点暴力连边,再用 kruskal 算法求解。时间复杂度约 $O(n^2log(n))$
注意到这种算法将许多没有意义的边连接了,所以我们需要分析如何才能高效地连接有意义的边。
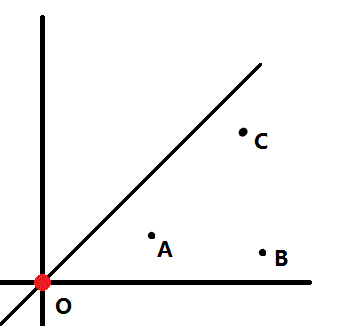
引理 1:对于一个点,我们只需要连接每个 1/8 象限内的离它最近的点。
需要证明若 A 为离 O 最近的点,连边 (O,A),(A,B) 比 (O,A),(O,B) 优,同时对于 C 也类似。
已知:$A_x+A_y<B_x+B_y$
需要证明:$(O,A)+(A,B)<(O,A)+(O,B)$
证:
因为:
$$
(O,A)+(A,B)=A_x+A_y+|B_x-A_x|+|B_y-A_y|
$$
$$
(O,A)+(O,B)=A_x+A_y+B_x+B_y
$$
所以只需证
$$
|B_x-A_x|+|B_y-A_y|<B_x+B_y
$$
拆开绝对值符号分别得到:
$$
-A_x-A_y<0
$$
$$
A_y-A_x<2B_y
$$
$$
A_x-A_y<2B_x
$$
$$
A_x+A_y<2B_x+2B_y
$$
分别都可以证明是对的。其他象限也可以如此证明。
因此我们已经证明了引理 1,就可以用它来建立生成树了。
寻找最近点
如何寻找最近的点成为了一个问题。如果我们遍历所有的点,与之前的暴力连边没有什么改进。因此我们会借助一定的遍历次序,和优秀的数据结构。
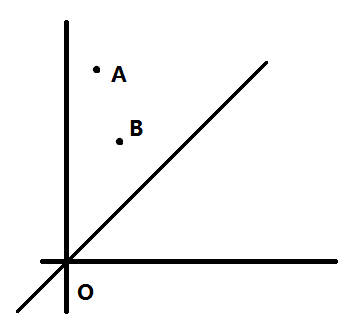
对于如图的 1/8 象限内的所有点 A, 离 O 最近的点一定是 $A_x+A_y$最小的那一个。为了找到那一个点,我们需要限制一下几个条件:
$$
A_y-A_x>=0
$$
$$
X>=0
$$
对于第一个条件,我们可以用线段树的区间表示,线段树的每一个区间 [a,b] 表示当前 A_y-A_x∈[a,b] 的所有点中 A_x+A_y 最小的一个。
对于第二个条件,我们可以按照 X 降序遍历。
至此,我们解决了所有问题,曼哈顿距离最小生成树问题也初步得到了解决。
扩展:
1. 如果点的范围比较大,需要进行离散化。
2. 对于动态更新的类似问题,请参考 http://www.doc88.com/p-998527952232.html
题目
一道裸题:51NOD1213 求曼哈顿距离最小生成树的边长度之和。
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#define MX 50005
#define MT 2000010
#define ME 1000005
#define MOV 1000001
#define oo 90000000
#define ls (node<<1)
#define rs (node<<1|1)
#define mid ((l+r)>>1)
#define dis(a,b) (abs((a).x-(b).x)+abs((a).y-(b).y))
using namespace std;
typedef struct point
{
int x,y,id;
}points;
typedef struct tnode
{
int mn,id;
}segtre;
points pot[MX];
segtre tre[MT<<2];
int fst[MX],nxt[ME],u[ME],v[ME],w[ME],lnum;
int fa[MX];
int ord[ME];
int n;
inline void addeg(int nu,int nv,int nw)
{
nxt[++lnum]=fst[nu];
fst[nu]=lnum;
u[lnum]=nu;
v[lnum]=nv;
w[lnum]=nw;
}
int findfa(int x)
{
return x==fa[x]?x:fa[x]=findfa(fa[x]);
}
inline void upd(int node)
{
if(tre[ls].mn<tre[rs].mn)tre[node].mn=tre[ls].mn,tre[node].id=tre[ls].id;
else tre[node].mn=tre[rs].mn,tre[node].id=tre[rs].id;
}
void build(int node,int l,int r)
{
tre[node].mn=+oo;
tre[node].id=-1;
if(l!=r)build(ls,l,mid),build(rs,mid+1,r);
}
void cng(int l,int r,int node,int p,int x,int id)
{
if(l==r)tre[node].mn=x,tre[node].id=id;
else if(p<=mid)cng(l,mid,ls,p,x,id),upd(node);
else cng(mid+1,r,rs,p,x,id),upd(node);
}
segtre qmn(int l,int r,int node,int ql,int qr)
{
segtre nul,a,b;
nul.mn=+oo;
nul.id=-1;
if(ql<=l&&r<=qr)return tre[node];
else if(ql>r||qr<l)return nul;
else
{
a=qmn(l,mid,ls,ql,qr);
b=qmn(mid+1,r,rs,ql,qr);
if(a.mn<b.mn)return a;
else return b;
}
}
inline bool cmpx(points a,points b)
{
return (a.x!=b.x)?(a.x>b.x):a.y>b.y;
}
inline bool cmpe(int a,int b)
{
return w[a]<w[b];
}
inline void sector1()
{
segtre near;
for(int i=1;i<=n;i++)
{
near=qmn(1,MOV<<1,1,MOV+pot[i].y-pot[i].x,+oo);
if(near.mn==+oo||near.id==-1);
else
{
addeg(pot[i].id,near.id,near.mn-pot[i].x-pot[i].y);
addeg(near.id,pot[i].id,near.mn-pot[i].x-pot[i].y);
}
cng(1,MOV<<1,1,MOV+pot[i].y-pot[i].x,pot[i].x+pot[i].y,pot[i].id);
}
}
long long cruskal()
{
long long ans=0,cnt=0;
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=lnum;i++)ord[i]=i;
sort(ord+1,ord+lnum+1,cmpe);
for(int i=1;i<=lnum;i++)
{
if(findfa(u[ord[i]])!=findfa(v[ord[i]]))
{
ans+=(long long)w[ord[i]];
cnt++;
fa[findfa(u[ord[i]])]=findfa(v[ord[i]]);
}
if(cnt>=n-1)break;
}
return ans;
}
void work()
{
sort(pot+1,pot+n+1,cmpx);
build(1,1,MOV<<1);
sector1();
for(int i=1;i<=n;i++)pot[i].x=-pot[i].x+MOV;
sort(pot+1,pot+n+1,cmpx);
build(1,1,MOV<<1);
sector1();
for(int i=1;i<=n;i++)swap(pot[i].x,pot[i].y);
sort(pot+1,pot+n+1,cmpx);
build(1,1,MOV<<1);
sector1();
for(int i=1;i<=n;i++)pot[i].y-=MOV,pot[i].y*=-1;
sort(pot+1,pot+n+1,cmpx);
build(1,1,MOV<<1);
sector1();
printf("%lld\n",cruskal());
}
void input()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d%d",&pot[i].x,&pot[i].y),pot[i].id=i;
}
int main()
{
input();
work();
return 0;
}
0 条评论