考试策略
原因竟然是做不出 T1 和 T2,只能去打 T3(麻将)的代码…(不不不,其实除了你别人都做出了 T1)
首先看了一下 T1 和 T2,都不是很有思路。于是 T1 打了 60 分暴力,T2 打了 40 分暴力,然后发现 T3 就是一个愚蠢的搜索。所以花了一个多小时的时间打了 T3, 检查一遍感觉没有什么问题,就交了。
T1
期望得分:60 实际得分:60
题目描述:
LargeDumpling 最近参加了志愿家教活动,结果第一次小朋友请假了,于是他在纸上玩起了矩阵。
LargeDumpling 在纸上写下了一个 n 行 m 列的 01 矩阵,他可以进行任意次交换任意两行的操作,他想找到操作后的最大的全 1 子矩阵。
LargeDumpling 在 1s 内就在脑中算出了结果,所以你的程序也需要在 1s 内得出结果。
数据范围:
对于 20% 的数据:$1 \leq n,m \leq 8$
对于 50% 的数据:$1 \leq n,m \leq 50$
对于 60% 的数据:$1 \leq n,m \leq 200$
对于 100% 的数据:$1 \leq n,m \leq 1000$
解题思路:
如果您是从 boshi 大佬的博客里过来的,请不要相信他的鬼话,我这里的满分算法也是 $O(n^2logn)$的
60 分就是枚举宽度的区间,预处理每一行前缀和后统计哪些行这一个区间都是 1,这个就是当前区间可能的宽度。
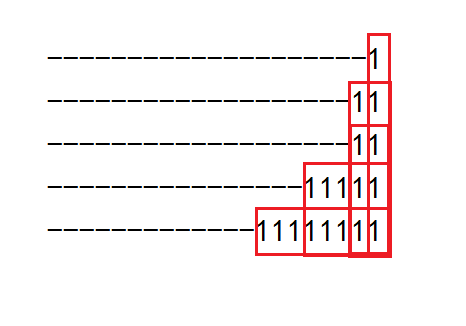
100 分算法感谢 xzy 大神的提供:对于每一个点,统计其左端有多少连续的 1. 然后枚举子矩阵的右端,将所有行的当前这一列其左端连续的 1 的数量排序,即移动该矩阵的行,使得当前列是一个三角形(如图),然后在这个三角形里找矩阵。
代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1005;
int n,m,a[N][N],cnt[N],tot[N],ans;
char ch[N][N];
int main(){
freopen("matrix.in","r",stdin);
freopen("matrix.out","w",stdout);
int i,j;
scanf("%d%d",&n,&m);
for(i=0;i<n;++i)scanf("%s",ch[i]);
for(i=0;i<n;++i)for(j=0;j<m;++j)a[i+1][j+1]=ch[i][j]-'0';
for(i=1;i<=m;++i){
for(j=1;j<=n;++j){
if(a[j][i])++cnt[j]; else cnt[j]=0;
tot[j]=cnt[j];
}
sort(tot+1,tot+1+n);
for(j=1;j<=n;++j)ans=max(ans,tot[j]*(n-j+1));
}
printf("%d",ans);
return 0;
}
T2
期望得分:40 实际得分:50
题目描述:
圣诞节快到了,jvjhfhg 开始思考给他的儿子们送礼物的事情。
jvjhfhg 有 m 个儿子,由于 Steam 游戏常常打折,他决定给他们买 Steam 游戏作为礼物。Steam 的打折游戏非常多,你可以认为有 无数件,jvjhfhg 根据价格将它们分成了 n 类,每一类的价格为 p i 。他的每个儿子给出了一个幸运数字 a i ,表示他希望得到价值和为 a i 的游戏。作为一个优秀的父亲,jvjhfhg 当然想要尽可能地满足所有儿子的要求,于是他想知道能满足多少个儿子的要求。
数据范围:
对于 30% 的数据:$n \leq 10,m \leq 100,p_i \leq 50,0 \leq a_i \leq 2*10^5$
对于 60% 的数据:$n \leq 100,p_i \leq 200$
对于另外 10% 的数据:n=2
对于 100% 的数据:$n \leq 500,m \leq 300000,p_i \leq 10000,0 \leq a_i \leq 4*10^7$
题目分析:
50 分啊,30% 数据可以一个完全背包瞎搞。10% 的数据可以一个扩欧再瞎搞,还有多出来的 10 分好像是我写的 “如果是所有礼物的公约数的倍数,就算作可以满足” 这样的一个骗分蜜汁多骗了 10 分?
而标解的思路是极其巧妙的。我们令物品里最小价格是 pmin,对于一个儿子的要求 x, 如果 x 模 pmin 的结果是 y,而除了最小价格物品以外的其他物品凑出一个模 pmin 结果是 y 的价格 z,这个价格比 x 小,则是 x 是可以凑出来的(因为 x-z 的部分可以通过使用 pmin 来完成)
那么怎么求其他物品凑一个模 pmin 答案为 y 的最小价格呢?答案居然是——最短路!
没错,就是最短路,每个取模后得到的数是节点,而路是除了最小价格物品以外的其他物品,路径长度是物品价格,路径终点要自己计算。
具体看代码吧,这题太巧妙了。
代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N=505,M=10005;
int n,m,ans;
int dis[M],inq[M],p[N];
void spfa(){
queue<int>q;int i,x,y;
for(i=1;i<=p[1];++i)dis[i]=5e8;
q.push(0),inq[0]=1;
while(!q.empty()){
x=q.front(),q.pop(),inq[x]=0;
for(i=2;i<=n;++i){
y=(x+p[i])%p[1];
if(dis[y]>dis[x]+p[i]){
dis[y]=dis[x]+p[i];
if(!inq[y])inq[y]=1,q.push(y);
}
}
}
}
int main(){
freopen("present.in","r",stdin);
freopen("present.out","w",stdout);
int i,x;
scanf("%d%d",&n,&m);
for(i=1;i<=n;++i)scanf("%d",&p[i]);
sort(p+1,p+1+n);spfa();
for(i=1;i<=m;++i){
scanf("%d",&x);
if(dis[x%p[1]]<=x)++ans;
}
printf("%d",ans);
return 0;
}
T3
期望得分:100 实际得分:35
题目描述:
AddEdge 最近沉迷日本麻将。
麻将是一个四人游玩的游戏。麻将牌由以下四类牌组成:
万子:一万至九万,我们用 1m~9m 表示。
索子:一索至九索,我们用 1s~9s 表示。
饼子:一饼至九饼,我们用 1p~9p 表示。
以上三种为数牌。
字牌:包括东、南、西、北、白、发、中七种牌,为了方便,我们依次用 1c~7c 表示。
以上每种牌各有 四张。
麻将和牌时有 14 张牌,和牌型通常为四面子加一雀头。面子是指顺子(三张同色且数字连续的数牌,如 1p 2p 3p 或 6m 7m 8m, 字牌不能形成顺子)或刻子(三张相同的牌,如 3s 3s 3s 或 5c 5c 5c),雀头是一对子即两张相同的牌(如 1m 1m 或 7c 7c)。
麻将中还有两种特殊和牌型:
七对子:由七个 不同的对子组成(日本麻将不承认 “龙七对” 手役,即一杠子加五对子)。
国士无双:由 1m 9m 1s 9s 1p 9p 1c 2c 3c 4c 5c 6c 7c 加上这十三张牌中的任意一张组成。
每局麻将开始时四名玩家各有 13 张牌,每一轮每名玩家摸一张牌并打出一张牌。当一副手牌再加上某一张牌构成一个和牌型时,我们称这副手牌听这张牌。
考虑一副未进行吃、碰、杠等鸣牌操作的手牌,判断这副手牌可以听哪些牌。 注意:在此题中, 不能再摸起的牌 即每种牌的第五张 不 能 算 作 听 的 牌
数据范围:
本题仅有 2 个测试点,采用 Special Judge 评分。
测试点均由 Part1、Part2 两部分组成
11 仅当全部正确时得分。
Part2(S2 分),每 X 个正确的数据得 1 分。
对于 Part2,为了防止骗分,每 Y 个输出”Nooten” 导致答案错误的数据会倒扣 1 分,最低不会低于 0 分
对于测试点 1(35 分):S1=10,S2=25,T=500,X=20,Y=10
对于测试点 2(65 分):S1=25,S2=40,T=10000,X=250,Y=100
解题思路:
出题人我***
不行不行,不能粗鲁,我要心平气和,我要做个淑女…
好吧,所谓解题思路,就是暴力特判国士无双和七对子,然后枚举添加的手牌,然后先确定雀头,再枚举面子。思路非常简单,代码虽然长但是写起来还是很畅快的(然而调起来并不畅快)
我经过一个多小时的写代码,调试,静态查错后确定此代码没有问题——但是我 TM 被卡了,第二个测试点 TLE,时限开大成 1.5s 就 A 了。
后来我才发现,原来枚举了一个顺子后,如果答案是不行,也直接 return 不用枚举下一对顺子,因为在优先枚举刻子的情况下,顺子只要枚举一对,接下来一定会枚举下一对,所以可以避免冗余操作。
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<climits>
using namespace std;
int T,ans;
int m[10],s[10],p[10],c[10];
int a[5][10];
int work1(){//国士无双
int js=0,i,bj1,bj2;
if(m[1])++js;else bj1=1,bj2=1;
if(m[9])++js;else bj1=1,bj2=9;
if(s[1])++js;else bj1=2,bj2=1;
if(s[9])++js;else bj1=2,bj2=9;
if(p[1])++js;else bj1=3,bj2=1;
if(p[9])++js;else bj1=3,bj2=9;
for(i=1;i<=7;++i)if(c[i])++js;else bj1=4,bj2=i;
if(js==13){
a[1][1]=a[1][9]=a[2][1]=a[2][9]=a[3][1]=a[3][9]=1;
for(i=1;i<=7;++i)a[4][i]=1;return 1;
}
else if(js==12){
if(m[1]==2||m[9]==2||s[1]==2||s[9]==2||p[1]==2||p[9]==2){a[bj1][bj2]=1;return 1;}
for(i=1;i<=7;++i)if(c[i]==2){a[bj1][bj2]=1;return 1;}
}
return 0;
}
void work2(){//七对子
int i,js=0,bj1,bj2;
for(i=1;i<=9;++i)
if(m[i]==2)++js;
else if(m[i]==1)bj1=1,bj2=i;
for(i=1;i<=9;++i)
if(s[i]==2)++js;
else if(s[i]==1)bj1=2,bj2=i;
for(i=1;i<=9;++i)
if(p[i]==2)++js;
else if(p[i]==1)bj1=3,bj2=i;
for(i=1;i<=7;++i)
if(c[i]==2)++js;
else if(c[i]==1)bj1=4,bj2=i;
if(js==6)a[bj1][bj2]=1;
}
int dfs(int d){//枚举面子
if(d==4)return 1;
int i,kl;
for(i=1;i<=9;++i)
if(m[i]>=3){m[i]-=3,kl=dfs(d+1),m[i]+=3;if(kl)return 1;}
for(i=1;i<=9;++i)
if(s[i]>=3){s[i]-=3,kl=dfs(d+1),s[i]+=3;if(kl)return 1;}
for(i=1;i<=9;++i)
if(p[i]>=3){p[i]-=3,kl=dfs(d+1),p[i]+=3;if(kl)return 1;}
for(i=1;i<=7;++i)
if(c[i]>=3){c[i]-=3,kl=dfs(d+1),c[i]+=3;if(kl)return 1;}
for(i=1;i<=7;++i)
if(m[i]&&m[i+1]&&m[i+2]){
--m[i],--m[i+1],--m[i+2],kl=dfs(d+1);
++m[i],++m[i+1],++m[i+2];if(kl)return 1;else return 0;
}
for(i=1;i<=7;++i)
if(s[i]&&s[i+1]&&s[i+2]){
--s[i],--s[i+1],--s[i+2],kl=dfs(d+1);
++s[i],++s[i+1],++s[i+2];if(kl)return 1;else return 0;
}
for(i=1;i<=7;++i)
if(p[i]&&p[i+1]&&p[i+2]){
--p[i],--p[i+1],--p[i+2],kl=dfs(d+1);
++p[i],++p[i+1],++p[i+2];if(kl)return 1;else return 0;
}
return 0;
}
void work4(int bj1,int bj2){//枚举雀头
int i;
for(i=1;i<=9;++i)
if(m[i]>=2){
m[i]-=2;if(dfs(0))a[bj1][bj2]=1;
m[i]+=2;if(a[bj1][bj2])return;
}
for(i=1;i<=9;++i)
if(s[i]>=2){
s[i]-=2;if(dfs(0))a[bj1][bj2]=1;
s[i]+=2;if(a[bj1][bj2])return;
}
for(i=1;i<=9;++i)
if(p[i]>=2){
p[i]-=2;if(dfs(0))a[bj1][bj2]=1;
p[i]+=2;if(a[bj1][bj2])return;
}
for(i=1;i<=7;++i)
if(c[i]>=2){
c[i]-=2;if(dfs(0))a[bj1][bj2]=1;
c[i]+=2;if(a[bj1][bj2])return;
}
}
void work3(){//枚举添加的牌
int i;
for(i=1;i<=9;++i)if(m[i]<4&&!a[1][i])++m[i],work4(1,i),--m[i];
for(i=1;i<=9;++i)if(s[i]<4&&!a[2][i])++s[i],work4(2,i),--s[i];
for(i=1;i<=9;++i)if(p[i]<4&&!a[3][i])++p[i],work4(3,i),--p[i];
for(i=1;i<=7;++i)if(c[i]<4&&!a[4][i])++c[i],work4(4,i),--c[i];
}
int main()
{
freopen("mahjong.in","r",stdin);
freopen("mahjong.out","w",stdout);
int i,j,t,ans;char ch[5];
scanf("%d",&T);
while(T--){
for(i=1;i<=9;++i)m[i]=s[i]=p[i]=c[i]=0;
memset(a,0,sizeof(a));
for(i=1;i<=13;++i){
scanf("%s",ch),t=ch[0]-'0';
if(ch[1]=='m')++m[t];
else if(ch[1]=='s')++s[t];
else if(ch[1]=='p')++p[t];
else ++c[t];
}
if(!work1())work2(),work3();
ans=0;
for(i=1;i<=3;++i)
for(j=1;j<=9;++j)if(a[i][j])++ans;
for(j=1;j<=7;++j)if(a[4][j])++ans;
if(!ans)puts("Nooten");
else {
printf("%d ",ans);
for(i=1;i<=9;++i)if(a[1][i])printf("%dm ",i);
for(i=1;i<=9;++i)if(a[2][i])printf("%ds ",i);
for(i=1;i<=9;++i)if(a[3][i])printf("%dp ",i);
for(i=1;i<=7;++i)if(a[4][i])printf("%dc ",i);
puts("");
}
}
return 0;
}
最后总结
要敢于承认自己的智障,并为了改变这一现况不断奋斗。
脚踏实地,艰苦努力,赢是我运,输是我命。
0 条评论