1. 题目
题目大意:
- 给一个静态序列,再给出 n 个操作,每个操作为求一个区间内第 k 小的数字是多少
2. 题解
以前写过一个二分套线段树的题解:传送门= ̄ω ̄=(题目一样,就是那个有多组数据这个没有)
那个复杂度是 $O(mlog_2^3n)$,比较慢
现在要讲的是主席树の做法,复杂度 $O(mlog_2n)$
先讲思路:
首先,如果我们要查询某段区间内的第 k 小数,我们可以采用二分答案!每次二分一个答案,判断这个数字在区间内排第几。比如我们有一个序列:$43241$,我们查询区间 $[2,5]$(即 $3241$)内排名第 $2$的是谁。我们先二分一个答案,比如是 $4$,发现 $4$排名为 $4$,所以答案比 $4$小。再二分,比如是 $1$(鬼知道它怎么二分成这样的),发现 $1$排名为 $1$,所以答案比 $1$大。这样下去就能找到最后答案为 $2$!
介于这个思想,我们用主席树来实现!
先对原序列 $a$(大小为 $n$)进行排序、去重得到序列 $h$,设序列 $h$内元素个数为 $tot$。我们对序列 $a$的前缀 $1,2,3,…,i(1\leq i\leq n)$分别建立一颗线段树(注意这里是线段树),一共有 $n$颗线段树。第 $i$颗线段树保存的是序列 $h$中的每个元素各在 $a$的前缀 $1,2,3,…,i$中出现了多少次!
比如序列 $a=45634$,那么 $h=3456$,则线段树对应表如下:
| 第几颗 | 对应序列 |
|---|---|
| 1 | 0100(增加了数字 4) |
| 2 | 0110(增加了数字 5) |
| 3 | 0111(增加了数字 6) |
| 4 | 1111(增加了数字 3) |
| 5 | 1211(增加了数字 4) |
大概看懂了吧,我尽力惹 QvQ
然后,比如我们要查询上面那个序列 $a=45634$的区间 $[2,5]$中的第 $2$小的数字是谁,于是我们拿出第 $2-1=1$颗线段树和第 $5$颗线段树,如图:
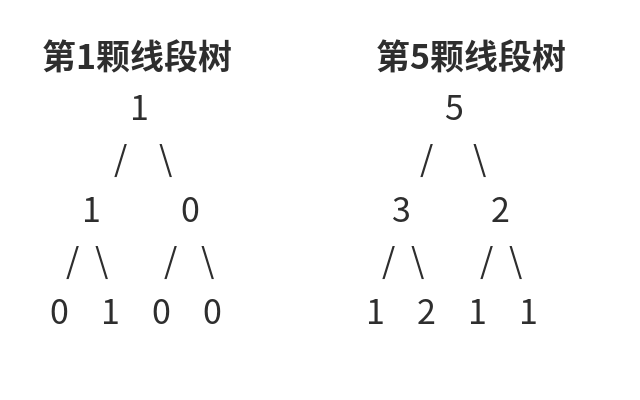
看懂了咩?其实就是俩维护区间和的线段树啊!(对应序列关系见上面的表格)
我们现在查第 $2$小数嘛,于是我们先到俩线段树的根节点看。根节点的左右儿子分别对应着 $h$序列的区间 $[1,2]$和 $[3,4]$,也就是 $34$和 $56$。可以看出来——在原序列 $a=45634$的区间 $[2,5]$(即 $5634$)中,34 一共出现了 2 次(3 有 1 次,4 有 1 次),正好是俩根节点的左儿子的权值之差($3-1=2$)。而 56 在区间 $[2,5]$中一共出现了 2 次(5 有 1 次,6 有 1 次),正好是俩根节点的右儿子的权值之差($2-0=2$)。所以我们可以轻松得到:在区间 $[l,r]$中,小于等于 4 的数字有 2 个,大于 4 的数字有 2 个。所以——我们就能知道——排名为 $2$的数字一定是在根节点的左儿子对应的区间内的!(3 和 4)
然后我们进入根节点的左儿子,发现——它的左儿子是对应序列 $h$中的 3,它的右儿子对应的是序列 $h$中的 4,其中小于等于 $3$的有 $1-0=1$个,而大于 $3$的有 $2-1=1$个(注意观察上图中的线段树),因此排名为 2 的数字在它的右儿子节点对于的 $h$序列区间中。
于是我们得到了最终答案——$h[2]=4$
这就是整个算法的全部原理。
由于我们需要 $n$颗线段树,但是显然没有这么多空间、时间,所以我们用可持久化线段树——主席树。
主席树原理我就不讲了,以后有空再总结一下了。
先安利一波教程(我在 B 站学算法 QvQ):传送门= ̄ω ̄=
好吧,讲了这么多,放个代码:
#include <cstdio>
#include <climits>
#include <cctype>
#include <algorithm>
#define NS (100005)
using namespace std;
template<typename _Tp>inline void IN(_Tp&dig)
{
char c;bool flag=0;dig=0;
while(c=getchar(),!isdigit(c))if(c=='-')flag=1;
while(isdigit(c))dig=dig*10+c-'0',c=getchar();
if(flag)dig=-dig;
}
struct N{int l,r,d;}t[NS*40];
int n,m,a[NS],h[NS],top,root[NS],cnt;
int H(int a){return lower_bound(h+1,h+1+top,a)-h;}
void update(int l,int r,int&x,int y,int pos)
{
x=++cnt,t[x]=t[y],t[x].d++;
if(l==r)return;
int mid=(l+r)>>1;
if(pos<=mid)update(l,mid,t[x].l,t[y].l,pos);
else update(mid+1,r,t[x].r,t[y].r,pos);
}
int query(int l,int r,int x,int y,int k)
{
if(l==r)return l;
int mid=(l+r)>>1,tmp=t[t[y].l].d-t[t[x].l].d;
if(tmp>=k)return query(l,mid,t[x].l,t[y].l,k);
return query(mid+1,r,t[x].r,t[y].r,k-tmp);
}
int main()
{
IN(n),IN(m),h[0]=INT_MAX;
for(int i=1;i<=n;i++)IN(a[i]),h[i]=a[i];
sort(h+1,h+1+n);
for(int i=1;i<=n;i++)if(h[i]!=h[i-1])h[++top]=h[i];
for(int i=1;i<=n;i++)update(1,n,root[i],root[i-1],H(a[i]));
for(int i=1,a,b,k;i<=m;i++)
IN(a),IN(b),IN(k),printf("%d\n",h[query(1,n,root[a-1],root[b],k)]);
return 0;
}
3 条评论
konnyakuxzy · 2018年1月7日 2:23 下午
QvQ 可是,,,您那篇文章会不会,,
不具有学术性&普遍性啊,这。。。
尴尬
Sys_Con · 2018年1月7日 11:10 上午
%%%Orz
— 来自刚学 Splay 的真蒟蒻
konnyakuxzy · 2018年1月7日 12:01 下午
QvQ Orz
我才是超级辣鸡啊=。=
连冬令营都没进 QvQ
我太菜惹 QvQ。。。
Kinandra · 2018年1月7日 2:05 下午
蒟蒻+1
Sys_Con · 2018年1月7日 2:06 下午
捕获一只谦虚 daolao
konnyakuxzy · 2018年1月7日 2:10 下午
Orz 泥萌太强惹,吓得我瑟瑟发抖不敢吱声 QvQ
Kinandra · 2018年1月7日 2:06 下午
SYSCON大师其实强的一毛
Kinandra · 2018年1月7日 2:07 下午
不过我才是吧爸爸
Kinandra · 2018年1月7日 2:08 下午
请忽略 ‘吧字 ‘
konnyakuxzy · 2018年1月7日 2:11 下午
Orz 您太聚惹 QvQ
话说泥萌是肿么找到我のblog 的啊?
很好奇=。=
Kinandra · 2018年1月7日 2:13 下午
聚是 J 的意思吗?
Kinandra · 2018年1月7日 2:14 下午
追问追问
konnyakuxzy · 2018年1月7日 2:15 下午
啊,其实是巨佬的意思。
所以。。。
泥萌是肿么找到我のblog 的啊?QAQ
Kinandra · 2018年1月7日 2:17 下午
是 SYS_CON 大神告诉我的
konnyakuxzy · 2018年1月7日 2:19 下午
不过不过,,,
泥萌不会认识我吧?QvQ
泥萌属于哪个学校啊 QvQ?
害怕.jpg
Kinandra · 2018年1月7日 2:23 下午
哈哈
不如你猜一猜
litble · 2018年1月4日 3:40 下午
赶紧在新年第一篇博客上留名,orz 大佬的主席树太强啦
konnyakuxzy · 2018年1月4日 4:09 下午
%%%KBdalao 访问我的辣鸡博客,真是令我不胜感激 Orz!
我的主席树还太垃圾了啊,您还能树状数组套主席树花式解决动态 kth 问题 Orz 太强啦
在新的一年里还是要多%%%kb 来 rp++!
Kinandra · 2018年1月7日 2:12 下午
xiang 大神怎么发文章啊???
Kinandra · 2018年1月7日 2:12 下午
(蒟蒻发出了疑问)
konnyakuxzy · 2018年1月7日 2:16 下午
蛤?
您认识我咩?
QvQ 害怕
写文章的话登录以后顶部有一个 “+新建” 按钮
点一下就行惹。
markdown 的
Kinandra · 2018年1月7日 2:18 下午
哦哦
我当然知道你呀
因为我是中情局的(划掉)
Kinandra · 2018年1月7日 2:19 下午
那它为什么总是” 待发布 “咩
konnyakuxzy · 2018年1月7日 2:20 下午
QvQ
这这这么强 QvQ
不会是我太弱了影响了市容吧 QvQ
其实是真的可以划掉的konnyakuxzy · 2018年1月7日 2:21 下午
QvQ 我我我我这就去审核 QvQ
毕竟,,,审核还是有必要的 QvQ。。。
konnyakuxzy · 2018年1月7日 2:23 下午
QvQ 可是,,,您那篇文章会不会,,
不具有学术性&普遍性啊,这。。。
尴尬
Kinandra · 2018年1月7日 2:24 下午
那就不要了吧
Kinandra · 2018年1月7日 2:24 下午
谢谢
Kinandra · 2018年1月7日 2:25 下午
你应该认识 kix6 吧
konnyakuxzy · 2018年1月7日 2:27 下午
QvQ 正在查找中 Orz
脑子不好使 ing
Kinandra · 2018年1月7日 2:28 下午
╮(╯▽╰)╭
Kinandra · 2018年1月7日 2:32 下午
好吧他其实是高三的大神
konnyakuxzy · 2018年1月7日 2:36 下午
Orz 查不到 QvQ
痛苦不堪
算惹算惹
但是,,泥萌为啥认识我啊?
我不是非常弱咩 QvQ
泥萌是一中的咩?
Kinandra · 2018年1月7日 2:40 下午
哈哈被你猜出来了
你很强的呦
konnyakuxzy · 2018年1月7日 2:44 下午
Orz 泥萌是,,,是,,,是高三 dalao?
Orz
跪舔泥萌 OrzOrzOrzOrz
大神啊 QvQ
konnyakuxzy · 2018年1月7日 2:46 下午
就说泥萌怎么会知道 “J”
QvQ
太强了
泥萌太 jay 了啊!
专门跑到蒟蒻的 blog 来嘲讽蒟蒻 Orz 太 jay 了
不过泥萌访问蒟蒻のblog 我还是非常感激的啦!
(*^__^*)
Kinandra · 2018年1月7日 2:46 下午
不是……
Kinandra · 2018年1月7日 2:47 下午
本蒟蒻还在 splay 的泥潭中挣扎
konnyakuxzy · 2018年1月7日 2:50 下午
,,,
想起来了
NYHdalao&LXYdalao?
Orz 跳绳の神犇啊!
QvQ 太强惹
爆踩我这种辣鸡蒟蒻 QvQ
Kinandra · 2018年1月7日 2:54 下午
哎呀不是呀
N 大佬都去准备冬令营了
Kinandra · 2018年1月7日 2:56 下午
看着高一大佬总以为我是初三大佬
不禁心生喜感
Kinandra · 2018年1月7日 2:56 下午
我不过是一个无名小卒
Kinandra · 2018年1月7日 2:57 下午
联赛差点一等都没了 QAQ
Kinandra · 2018年1月7日 2:59 下午
不过 LXYdalao 在我旁边哦
Kinandra · 2018年1月7日 3:00 下午
你肯定不认识我的咩
konnyakuxzy · 2018年1月7日 3:01 下午
QvQ 我不说话惹
再膜下去我要把地球人全% 一遍惹
QvQ
不过您 QQ 显示是,,,14 岁???
太强了%%%%Orz
Kinandra · 2018年1月7日 3:09 下午
啊啊暴露年龄了 QAQ
Kinandra · 2018年1月7日 3:40 下午
X 大佬在 6 机房咩??
Kinandra · 2018年1月7日 3:42 下午
大佬??
在?
回一句吧
不耍大佬了
konnyakuxzy · 2018年1月7日 6:14 下午
Orz 刚刚更新博客去啦~
才看到 Orz
您耍我完全没问题的啦~QvQ
但是您别说我是 dalao 啊,这样是在侮辱 dalao 这个词啊 QAQ
【题解】 Dynamic Rankings 动态区间第k小问题 二分答案+树套树(线段树套splay) BZOJ – 1901 | K-XZY · 2018年1月4日 4:03 下午
[…] 主席树:传送门= ̄ω ̄= […]